Function Repository Resource:

MultiPerspectiveEmbedding

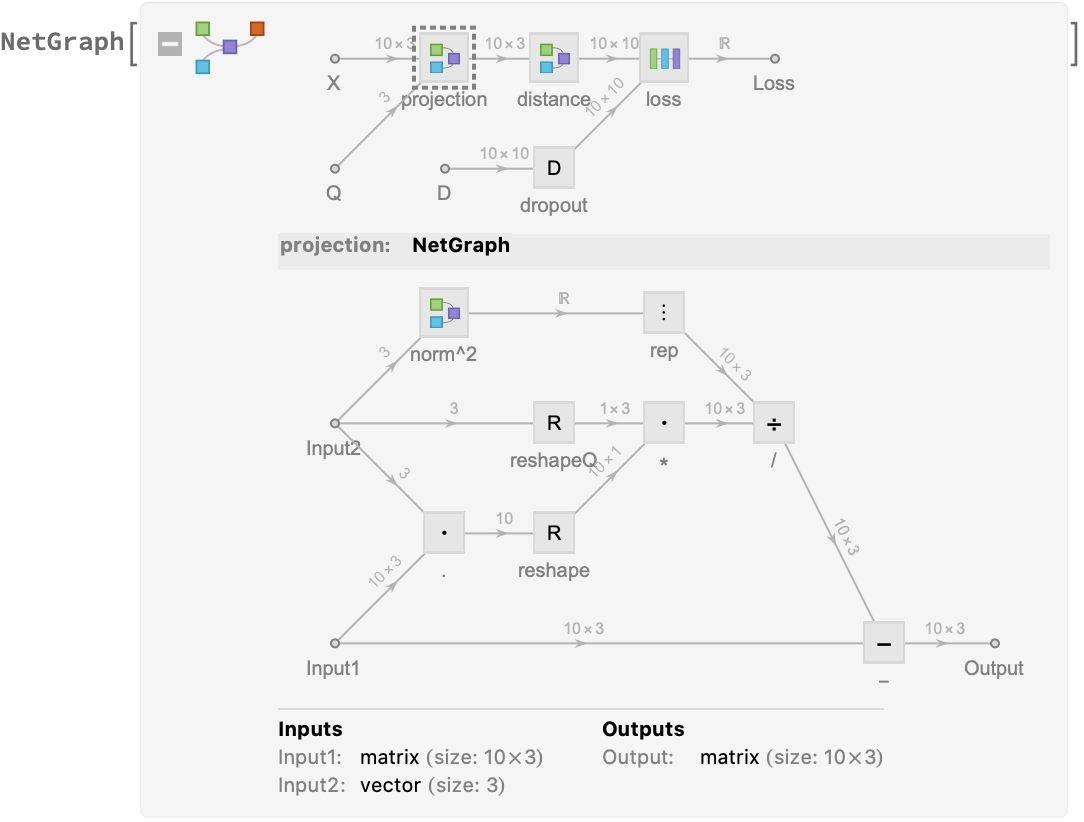
Compute a 3D embedding for multiple graphs so that all pairwise distances are preserved simultaneously along various 2D projections

Contributed by: Nikolay Murzin

ResourceFunction["MultiPerspectiveEmbedding"][gs]

gives multi-perspective 3D embedding of graphs gs.

ResourceFunction["MultiPerspectiveEmbedding"][ds]

gives multi-perspective 3D embedding for explicit distance matrices.

Details and Options

The Graph inputs gs should have the same set of vertices.

Distance matrices ds should be square and of the same dimensions.

ResourceFunction["MultiPerspectiveEmbedding"] accepts the following options:

"InitialEmbedding"

Automatic

array of initial embedding vectors

"InitialProjection"

Automatic

array of initial normal vectors

"FixProjection"

False

whether to fix or learn projection vectors

"UseGraphEmbedding"

True

if the input is graphs, whether to use its embeddings for computing distances

"NormalizeDistances"

True

whether to normalize distances

"NetTrainOptions"

{}

custom options for NetTrain

TrainingProgressReporting

Automatic

use "Verbose" for custom reporting

This is an elementary layer for training embeddings X, with one projection normal vector Q and a distance matrix D.

Examples

Basic Examples (3)

Compute a 3D embedding for a grid graph and a path graph:

In[1]:=

$ResourceFunction[ "MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}]$

Out[1]=

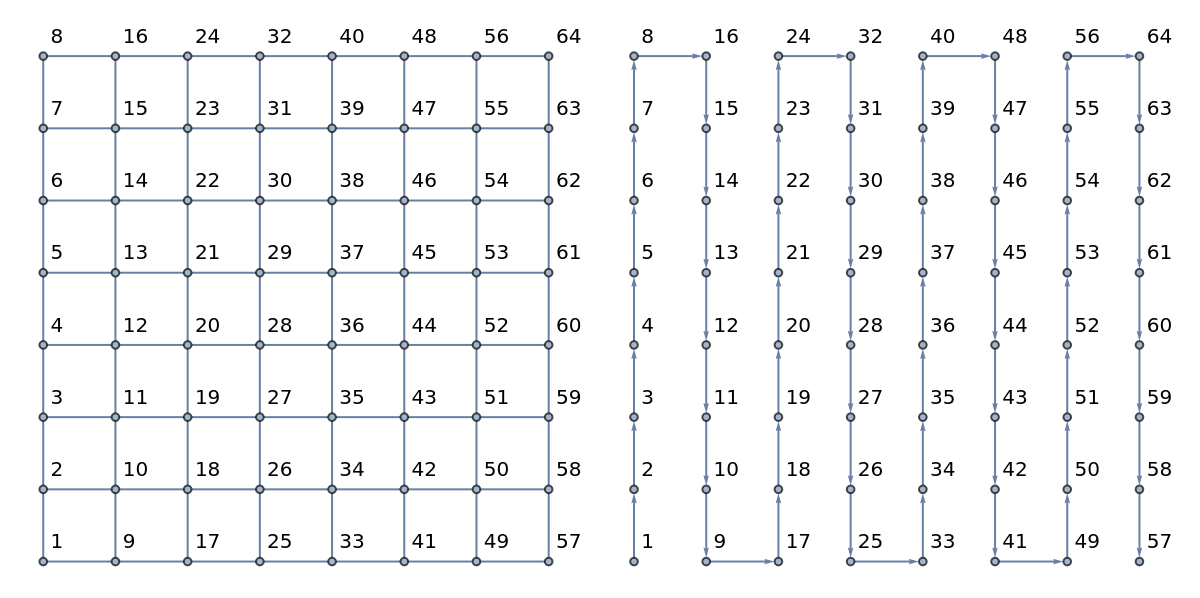
Define larger grid and path graphs and show them:

In[2]:=

$With[{n = 8}, g1 = GridGraph[{n, n}, VertexLabels -> Automatic]; g2 = Graph[VertexList[g1], DirectedEdge @@@ Partition[ Catenate@ MapAt[Reverse, Partition[Range[n^2], n], List /@ Range[2, n, 2]], 2, 1], VertexCoordinates -> GraphEmbedding[g1], VertexLabels -> Automatic] ]; GraphicsRow[{g1, g2}]$

Out[3]=

Compute an embedding:

In[4]:=

Out[4]=

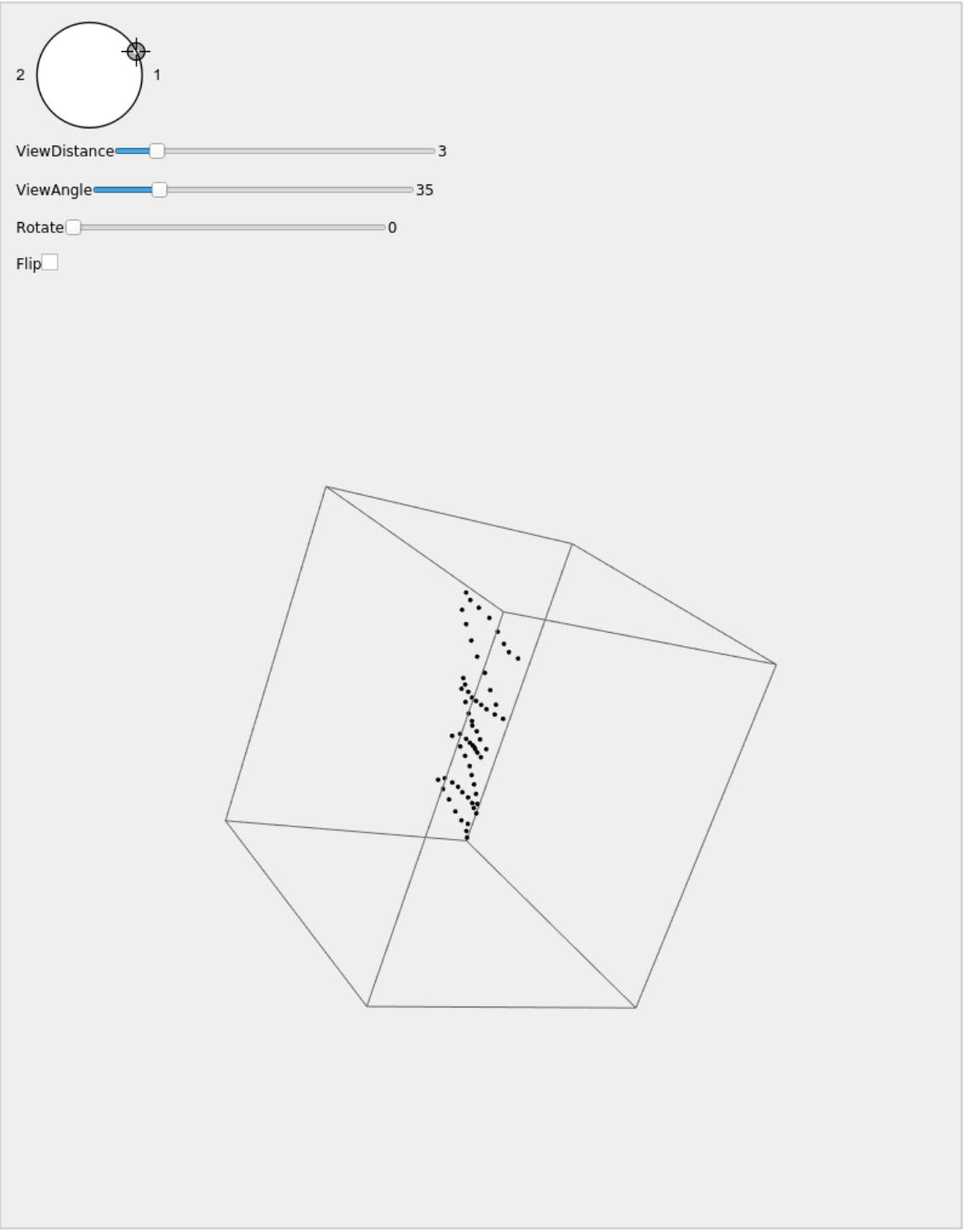
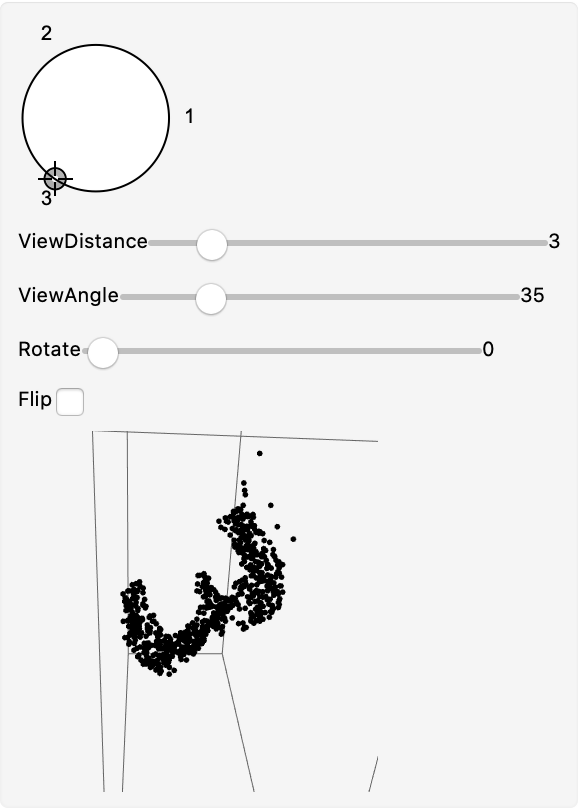
View the embedding with the resource function MultiPerspectiveEmbeddingViewer:

In[5]:=

ResourceFunction["MultiPerspectiveEmbeddingViewer"][graphMPSE, "DisplayFunction" -> Function[Graphics3D[Point@graphMPSE["Embedding"], ##, AspectRatio -> 1, ImageSize -> Large]]]

Out[5]=

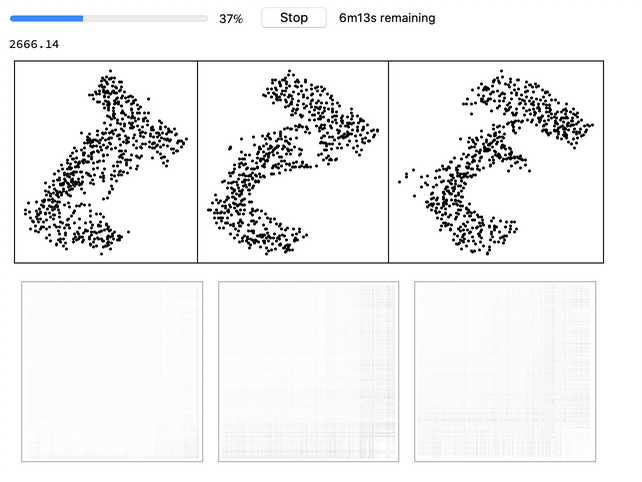
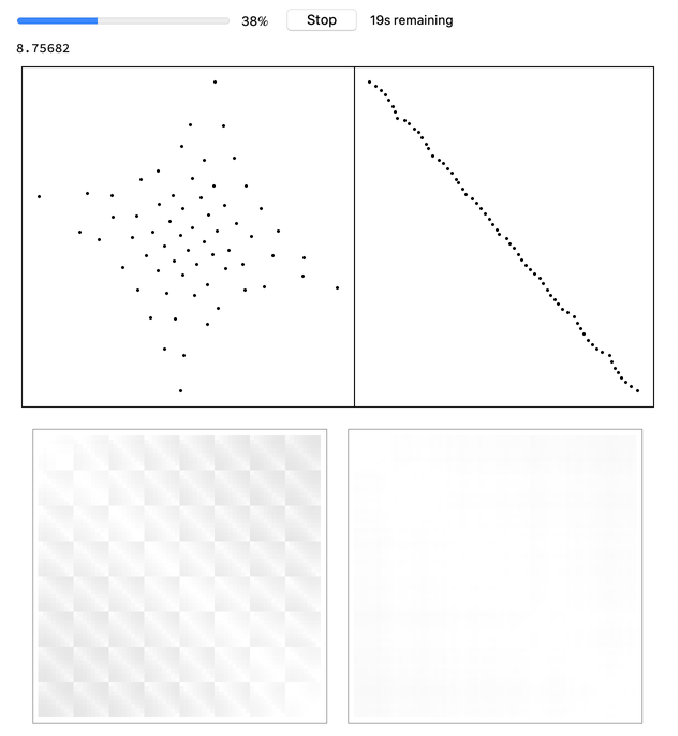
Here is the progress for training an embedding for points that look like digits 1, 2 and 3 in 2D from three distance matrices and how they form into their position:

In[6]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/4870c165-3fd6-4c47-b61e-50d7be9ad395"]

View the embedding:

In[7]:=

Out[7]=

Options (7)

NetTrainOptions (1)

Specify custom options for NetTrain, for example, MaxTrainingRounds:

In[8]:=

$ResourceFunction[ "MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 1}]$

Out[8]=

InitialEmbedding (1)

Specify an initial embedding:

In[9]:=

$ResourceFunction[ "MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 1}, "InitialEmbedding" -> Append[0] /@ GraphEmbedding[GridGraph[{4, 4}]]]$

Out[9]=

InitialProjection (1)

Specify initial normal projection vectors using the "InitialProjection" option. The "Normals" key of the resulting association would contain new projection normal vectors after training:

In[10]:=

$ResourceFunction[ "MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 10}, "InitialProjection" -> {{1, 0, 0}, {0, 1, 0}}]$

Out[10]=

FixProjection (1)

Disable learning for normal vectors. The "Normals" value stays the same:

In[11]:=

$ResourceFunction[ "MultiPerspectiveEmbedding"][{GridGraph[{4, 4}], PathGraph[Range[4^2]]}, "NetTrainOptions" -> {MaxTrainingRounds -> 1}, "InitialProjection" -> {{1, 0, 0}, {0, 1, 0}}, "FixProjection" -> True]$

Out[11]=

UseGraphEmbedding (2)

By default, distances are taken to be the distances between its graph embeddings:

In[12]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9de89ea1-9427-41af-b85f-a0d9570d2caa"]

UseGraphEmbedding → False would use GraphDistanceMatrix instead:

In[13]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/9678d836-0077-4e6d-8e9a-08b1ef083799"]

NormalizeDistances (1)

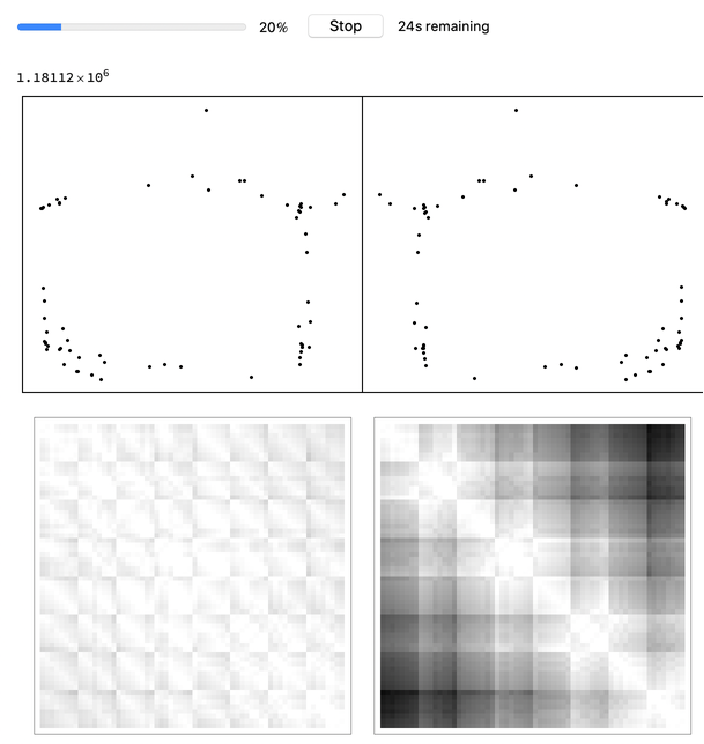
Without normalizing distances, training may diverge:

In[14]:=

(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7e55aa1e-38dc-4fe9-beb2-48e33ecbcd21"]

Publisher

N. Murzin

Version History

2.0.0 – 21 January 2021
1.0.0 – 17 July 2020

Source Metadata

Citation:
- Hossain, M.I., Huroyan, V., Kobourov, S.G., & Navarrete, R. (2019). Multi-Perspective, Simultaneous Embedding. ArXiv, abs/1909.06485.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

MultiPerspectiveEmbedding

Details and Options