Basic Examples (6)
Construct a simple abstract category from an association of arrows/morphisms:
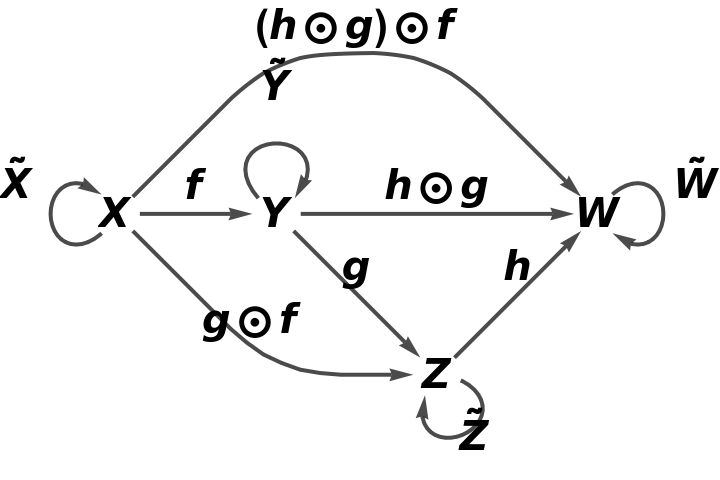
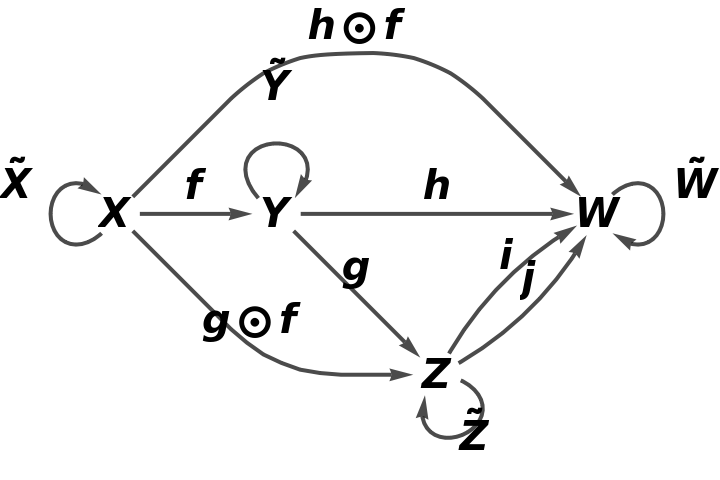
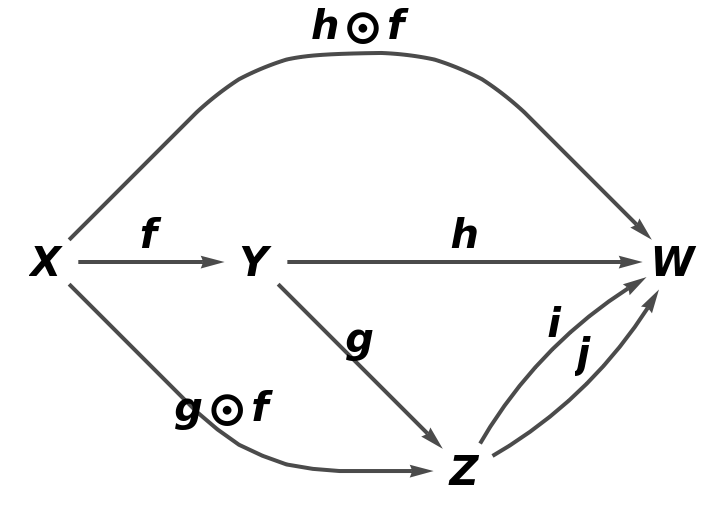
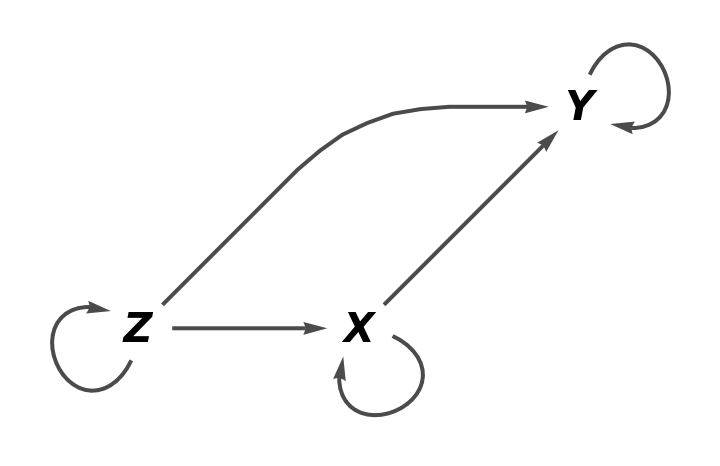
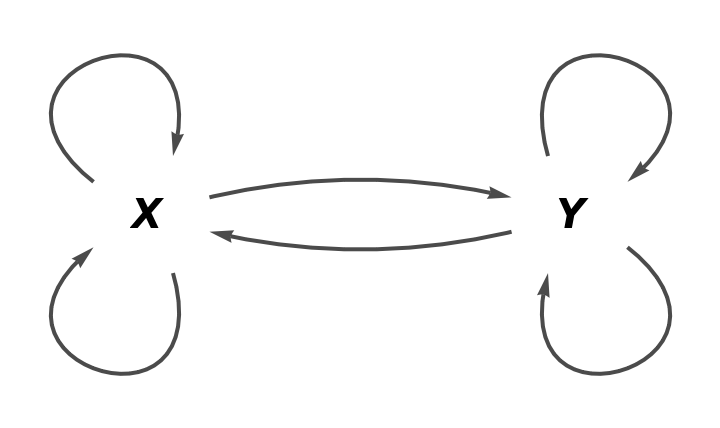
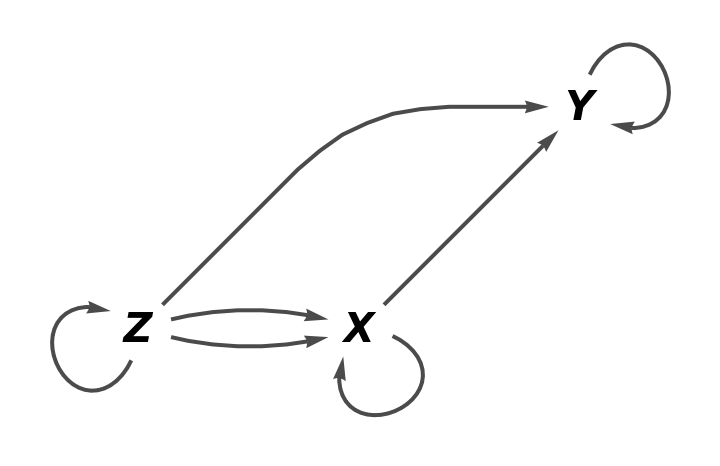
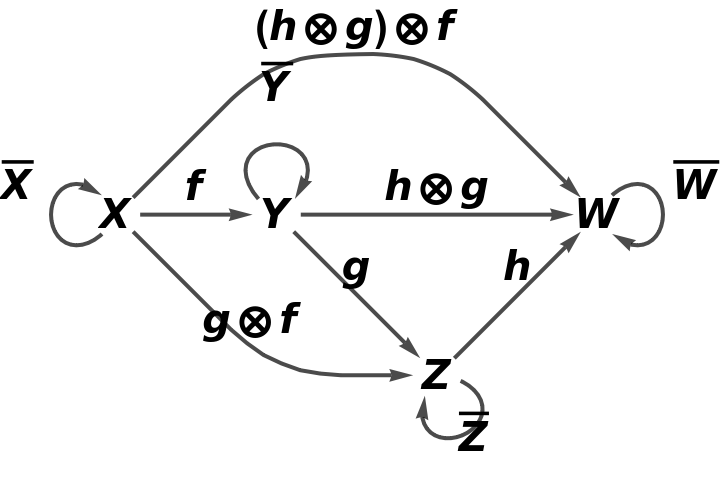
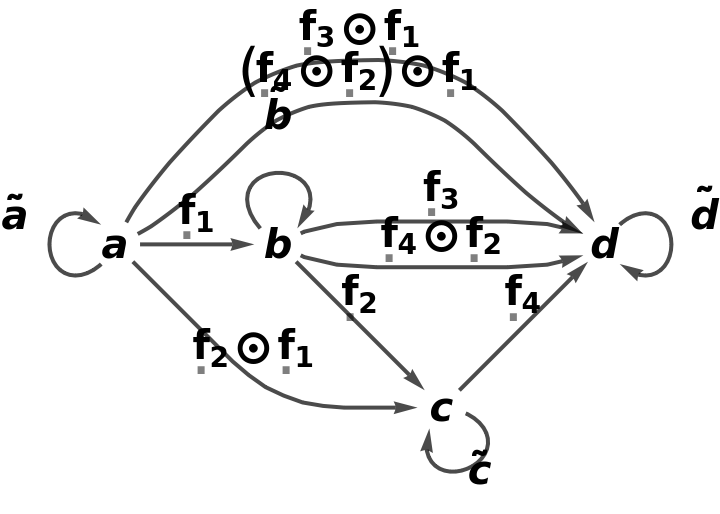
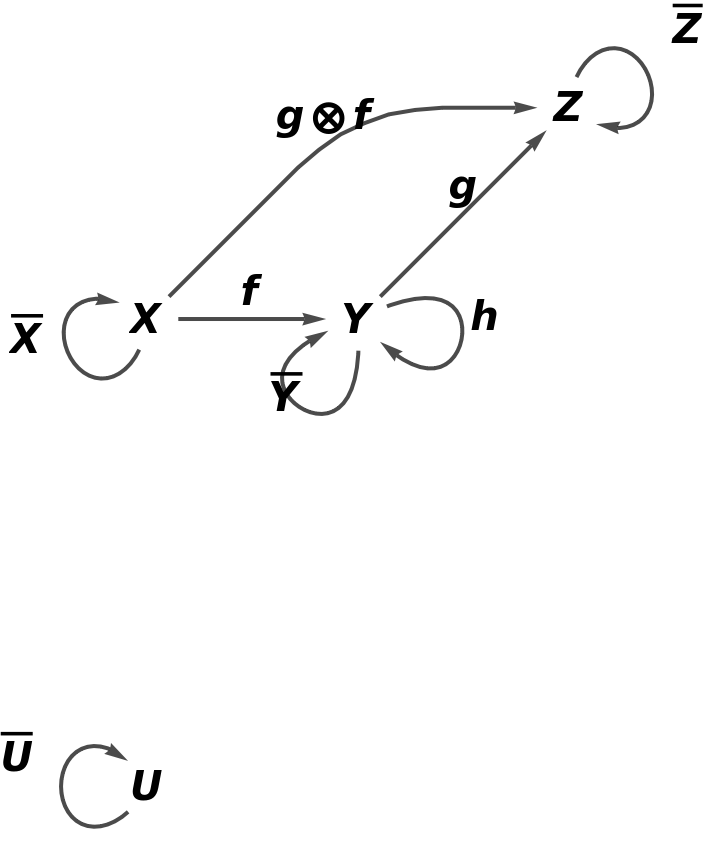
Show the full directed graph with labels on the morphisms:
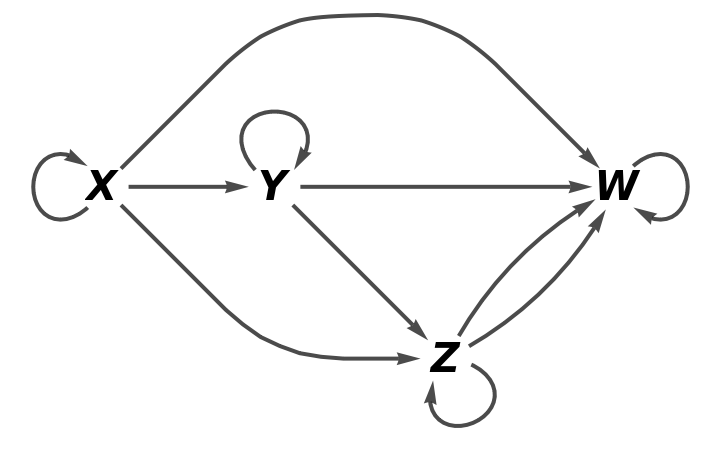
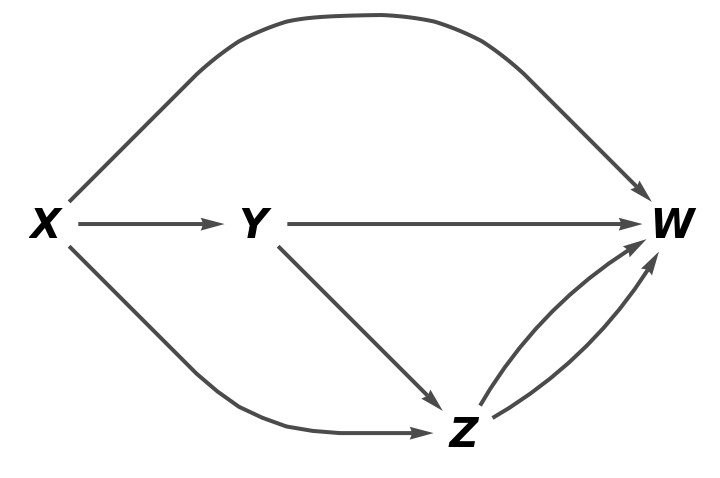
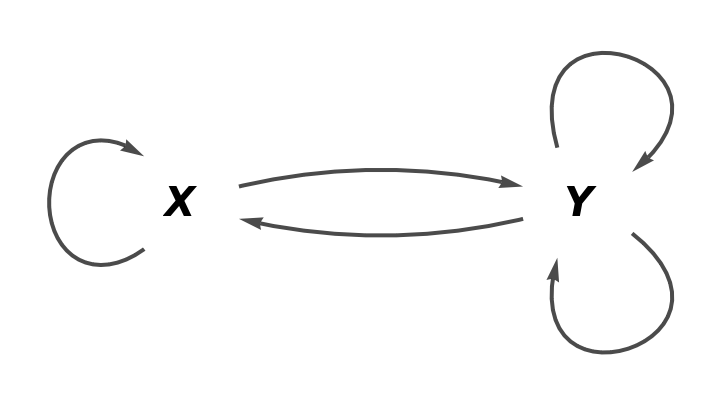
Show the full directed graph without labels on the morphisms:
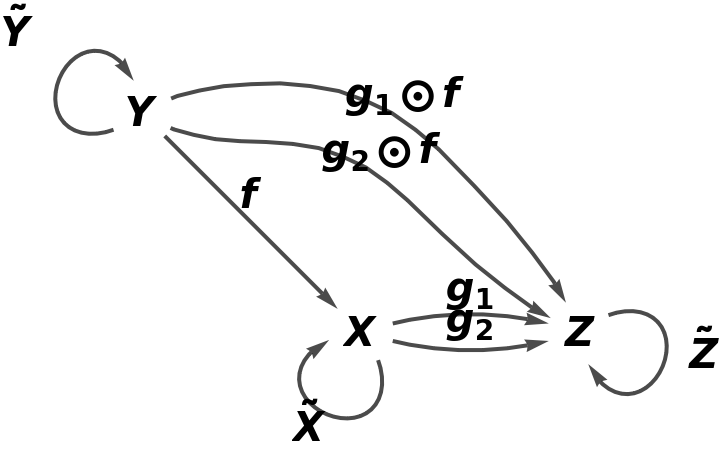
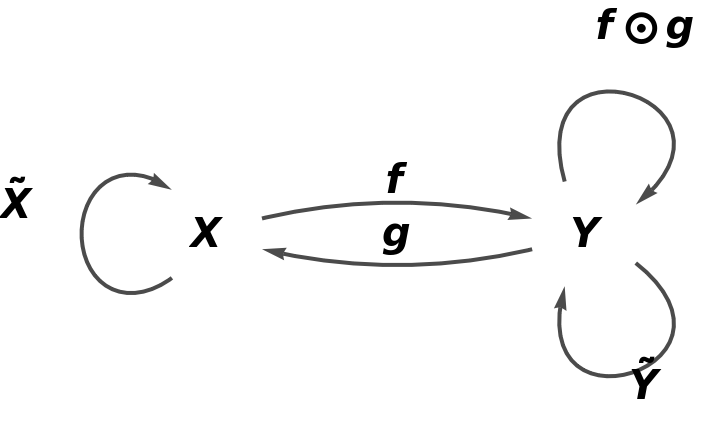
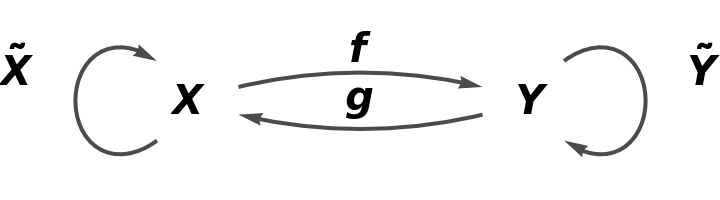
Show the association of morphisms:
Show the list of directed edges:
Construct the same abstract category, but with new composition and identity symbols ⊗ and ─, and with an equivalence imposed between objects X and Y and morphisms g⊗f and g:
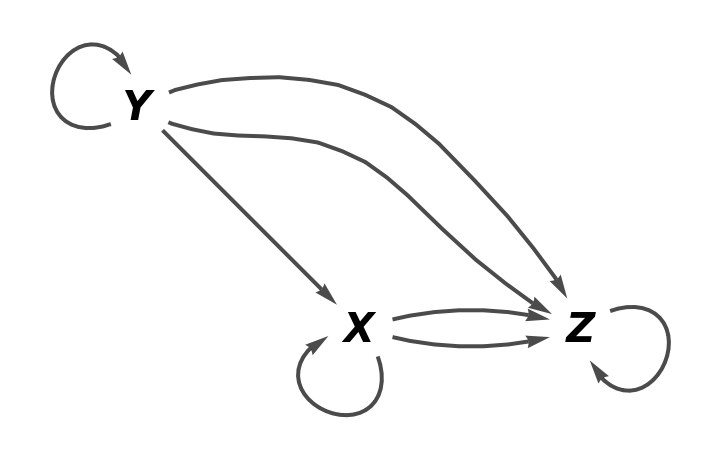
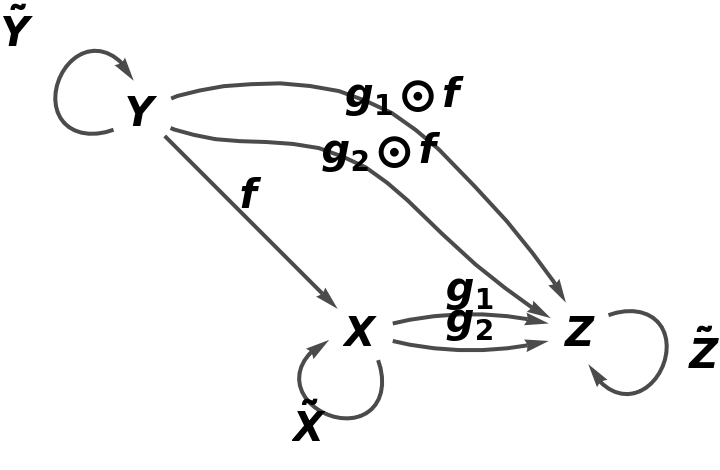
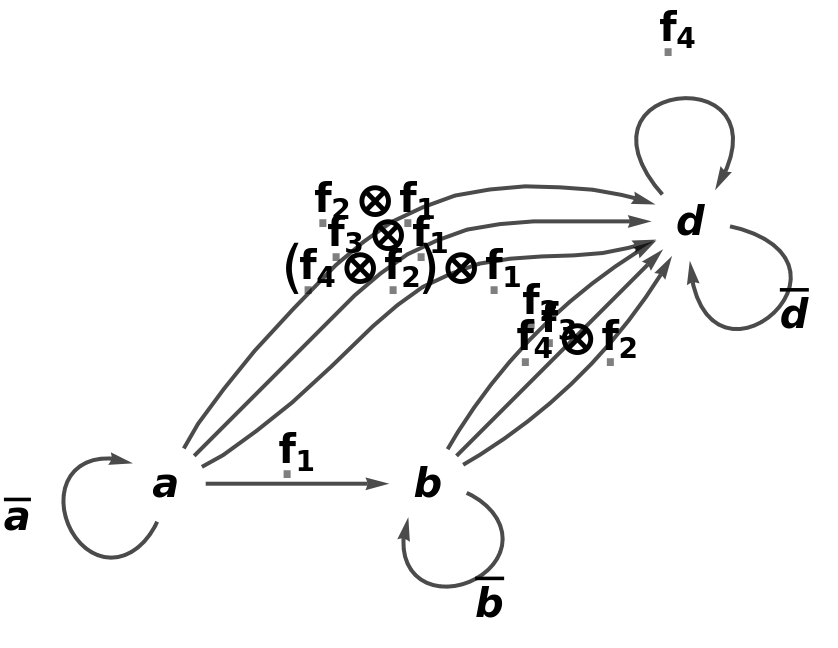
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graph without labels on the morphisms:
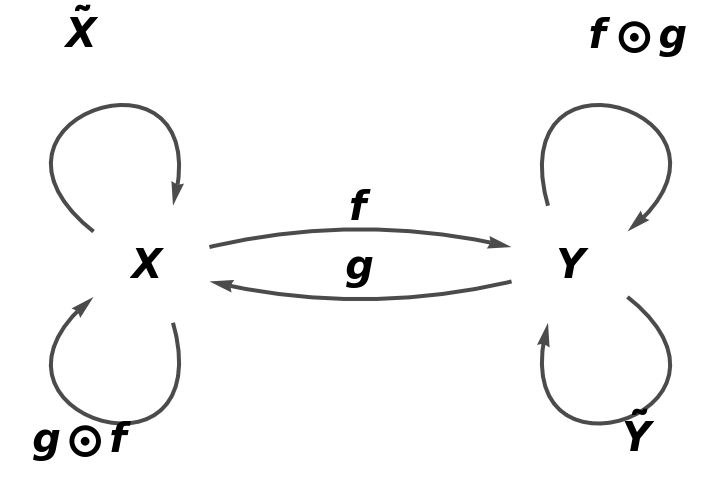
Show the association of morphisms, with all equivalences between objects and morphisms imposed:
Show the list of equivalences between objects:
Show the list of equivalences between morphisms:
Show the association form of the abstract category:
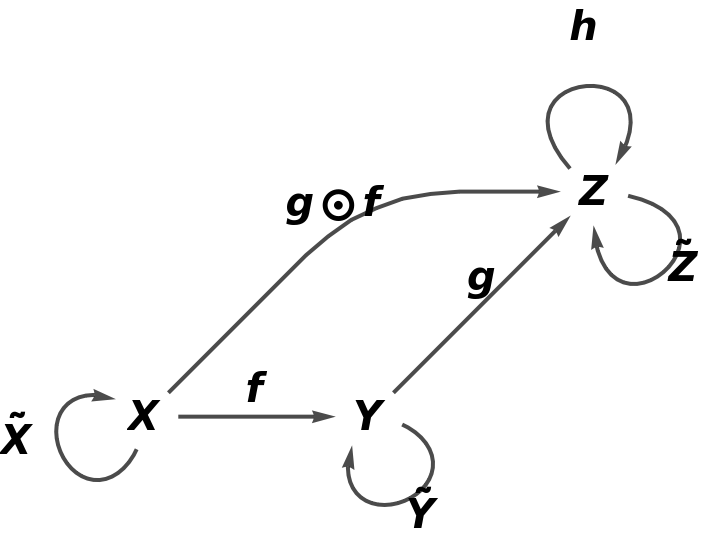
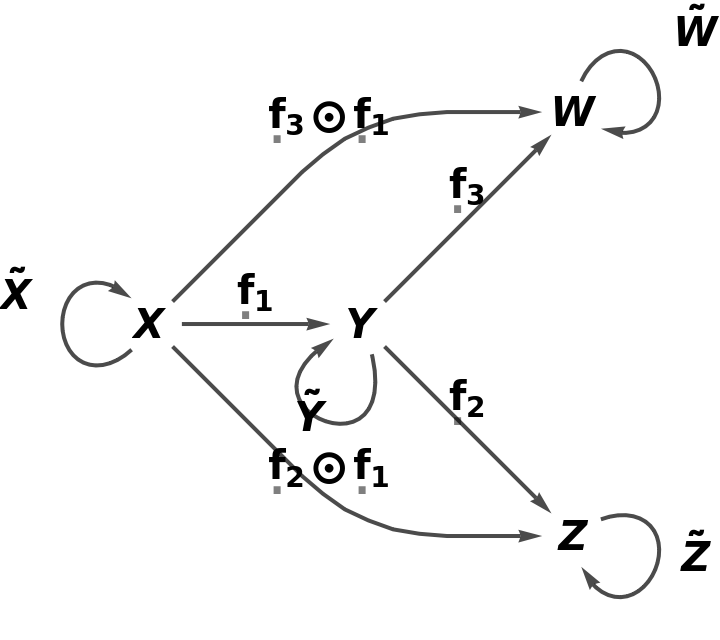
Construct an abstract category from a square-shaped quiver:
The corresponding abstract category:
Show that the resulting square is not commutative:
Compute the list of equations between morphisms that must hold for the square to be commutative:
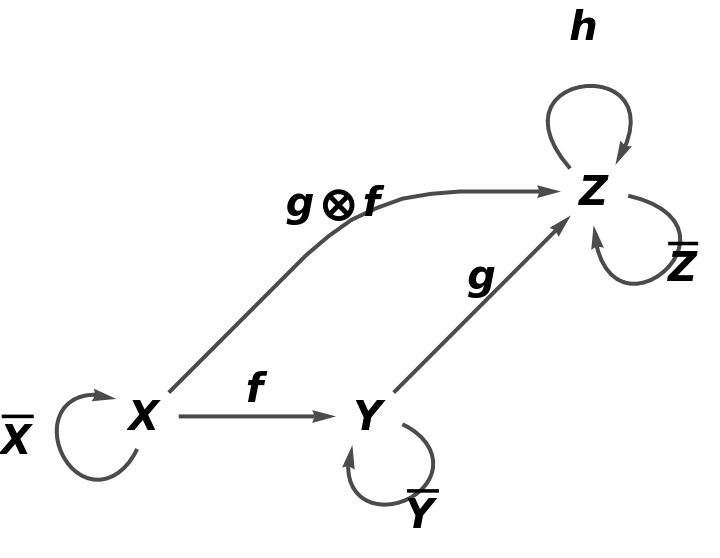
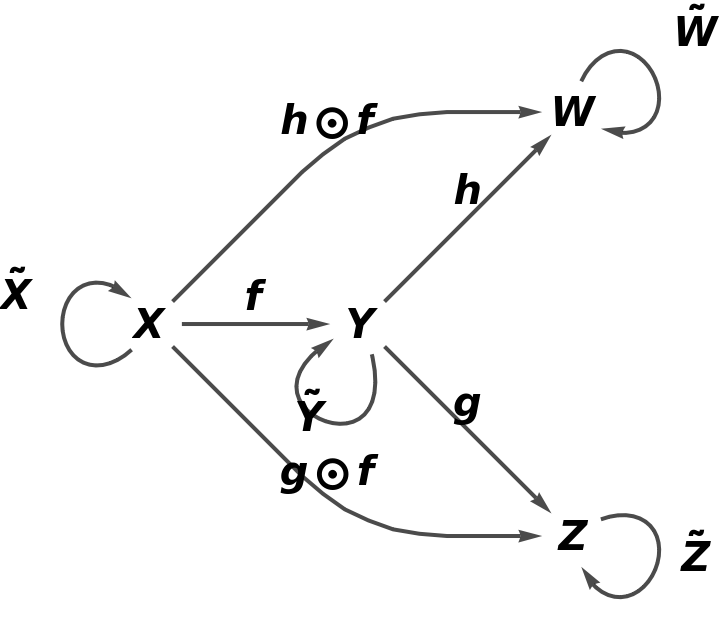
Construct the same abstract category, but with the aforementioned equivalence between morphisms h⊙f and i⊙g imposed:
Show that the resulting square is now commutative:
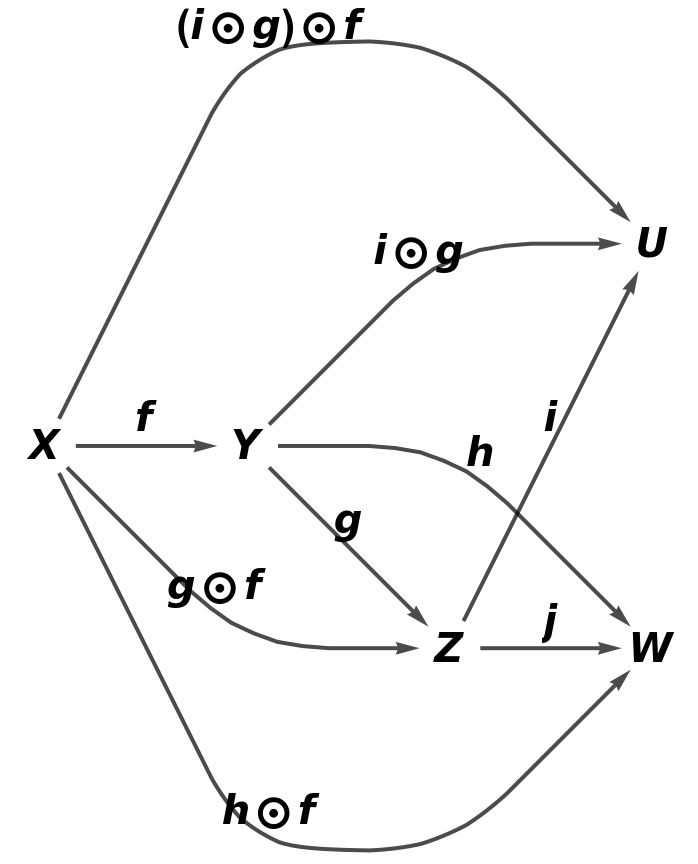
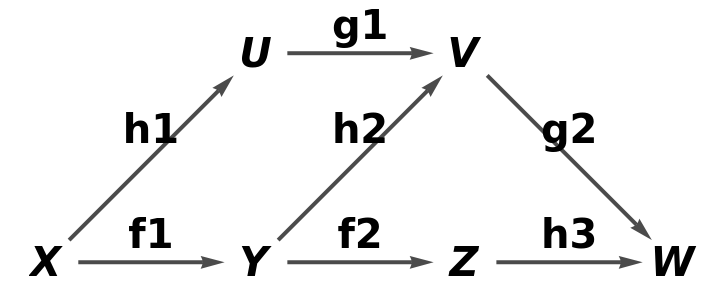
Construct an abstract category from an oblong-shaped quiver:
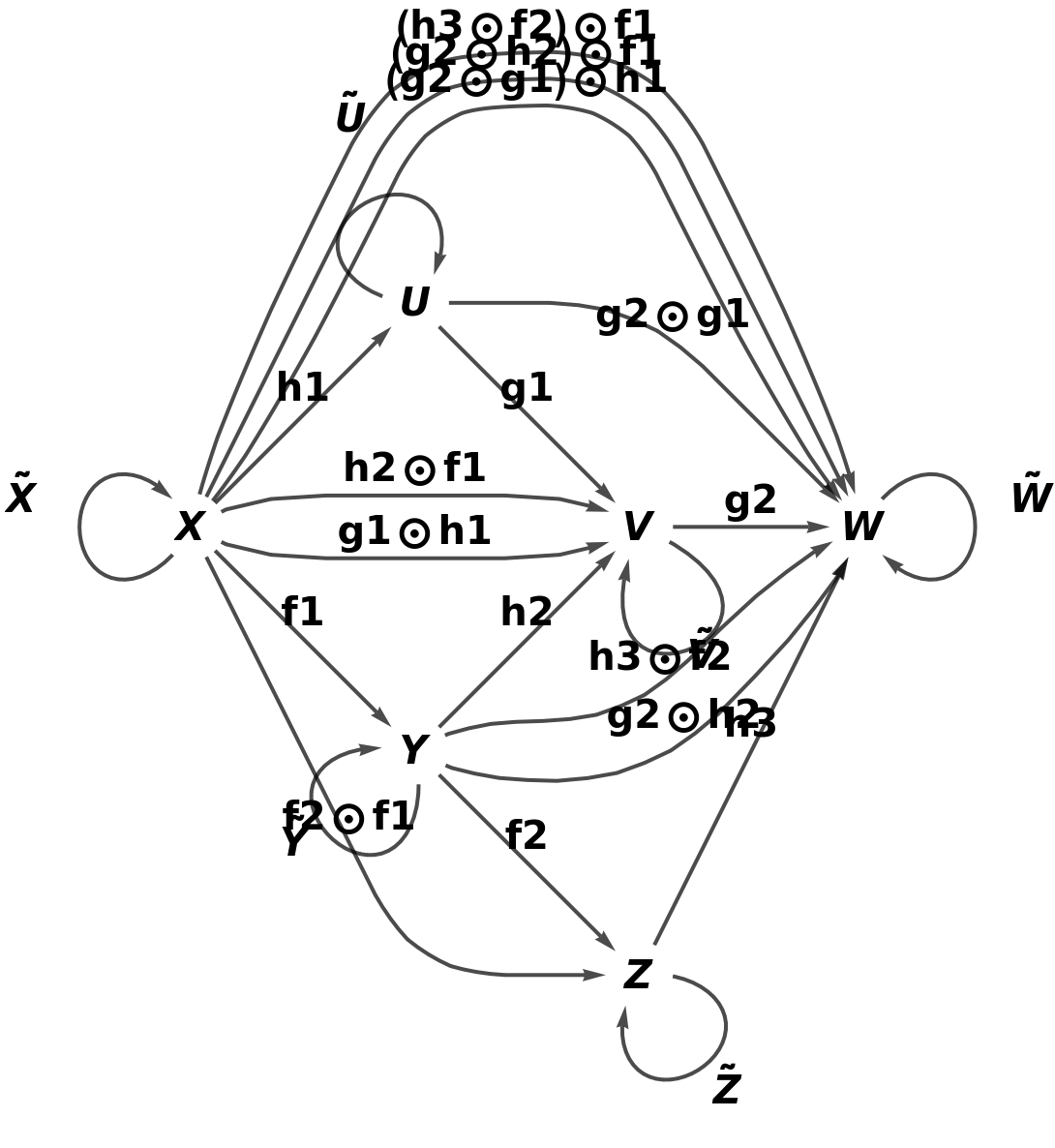
The corresponding abstract category:
Compute the list of equations between morphisms that must hold for the oblong to be commutative:
Compute the list of equations between morphisms that must hold by virtue of morphism composition being associative:
Compute the list of equations between morphisms that must hold by virtue of all objects having an identity morphism:
Construct an abstract category consisting of a pair of parallel morphisms g1 and g2 and a third morphism f leading out from them, together with an equivalence between morphisms f⊙g1 and f⊙g2:
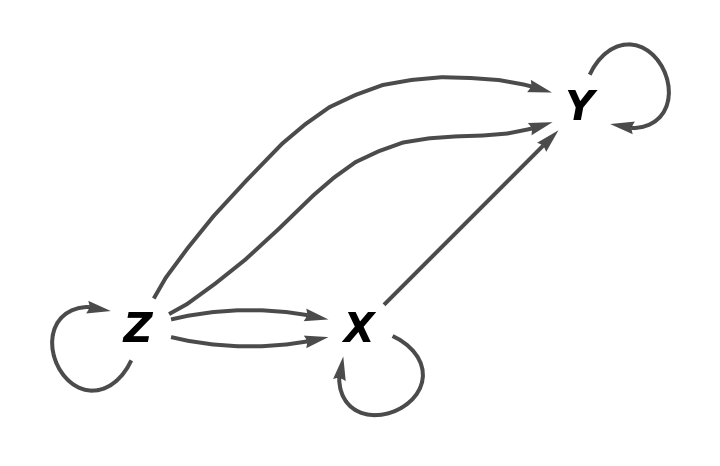
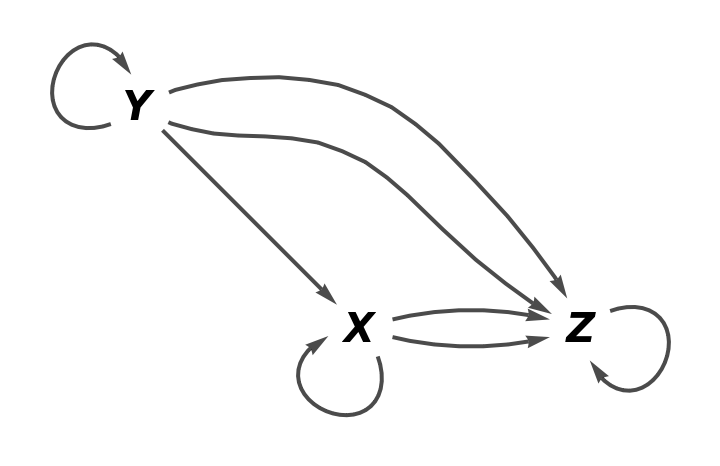
Show the full directed graph with labels on the morphisms:
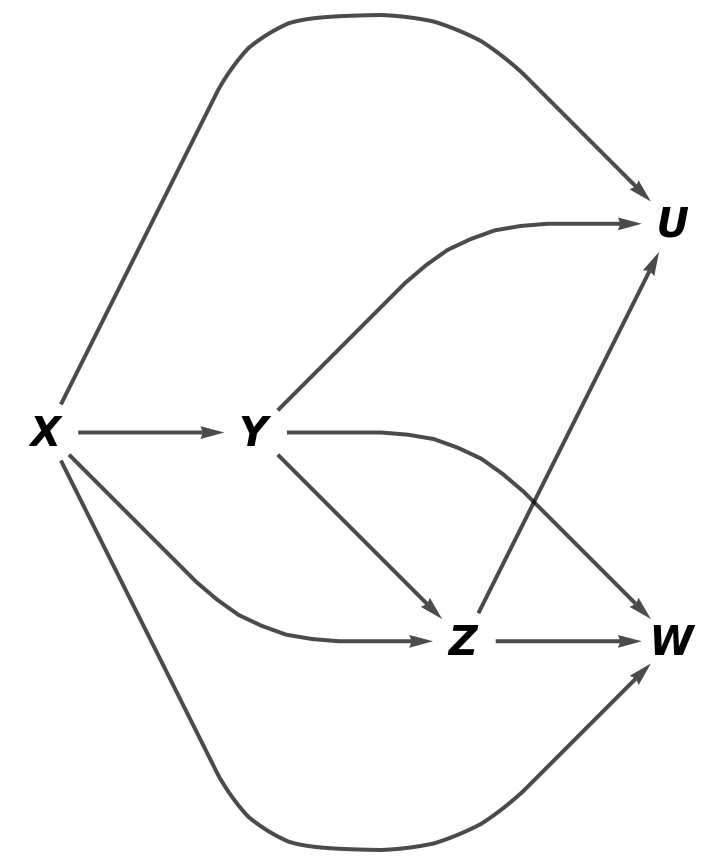
Show the full directed graph without labels on the morphisms:
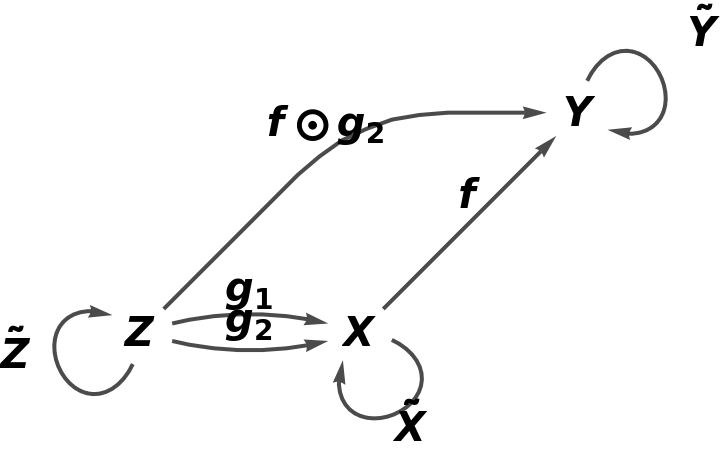
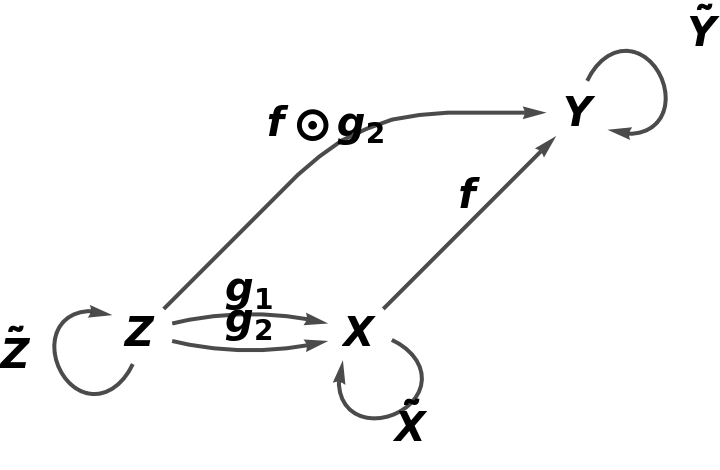
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graph without labels on the morphisms:
Show the association of monomorphisms (i.e. left-cancellative/injective morphisms), illustrating that f is not a monomorphism:
Construct the same abstract category, but with an additional equivalence imposed between morphisms g1 and g2, thus forcing f to be a monomorphism:
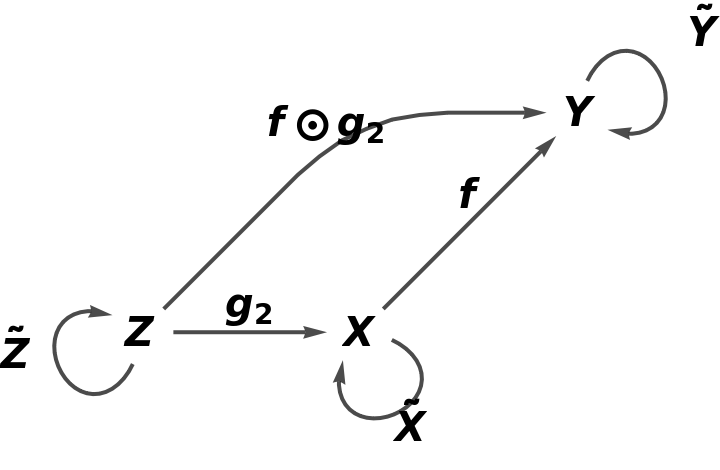
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graph without labels on the morphisms:
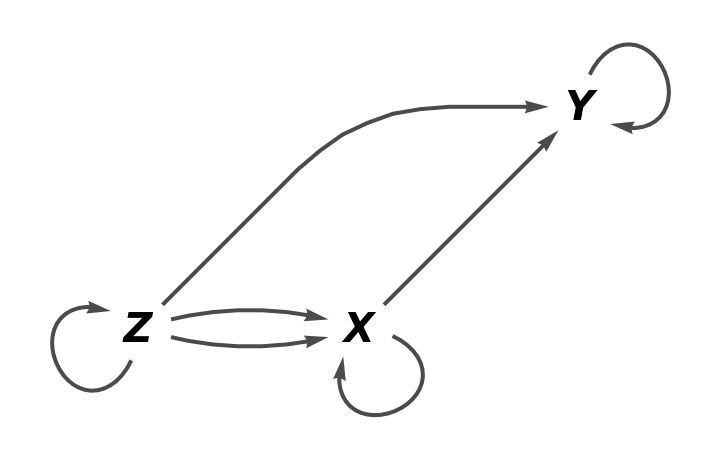
Show that f is now a monomorphism:
Show the association of monomorphisms modulo all equivalences between objects and morphisms:
Every monomorphism is an epimorphism (i.e. a right-cancellative/surjective morphism) in the dual category:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show the association of bimorphisms (i.e. left- and right-cancellative/bijective morphisms) in the original category, illustrating that f is not a bimorphism:
Show the association of bimorphisms modulo all equivalences between objects and morphisms:
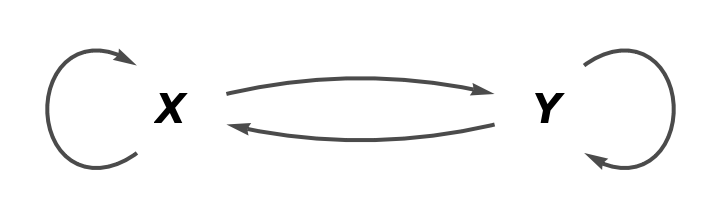
Construct an abstract category consisting of a pair of morphisms f and g leading between objects X and Y in opposite directions:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show that neither f nor g is a retraction (i.e. a left inverse) nor a section (i.e. a right inverse), and therefore is also not an isomorphism (i.e. a left and right inverse):
Construct the same abstract category, but with an equivalence imposed between morphisms g⊙f and the identity on object X:
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced labeled graph without labels on the morphisms:
Show that g is now a retraction and f is now a section, though neither is an isomorphism:
Show, equivalently, that g is a left inverse of f and f is a right inverse of g, but neither is a full inverse of the other:
Construct the same abstract category, but with an additional equivalence imposed between morphisms f⊙g and the identity on object Y:
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graph without labels on the morphisms:
Show that f is now a retraction and g is now a section, and both are now isomorphisms:
Show, equivalently, that f is now both a left and right inverse of g, and vice versa:
Show the associations of retractions, sections and isomorphisms modulo all equivalences between objects and morphisms:
Show the associations of left inverses, right inverses and "full" inverses modulo all equivalences between objects and morphisms:
Show that the category is therefore a groupoid (i.e. all morphisms are isomorphisms):
Show that the category is also balanced (i.e. all bimorphisms are also isomorphisms):
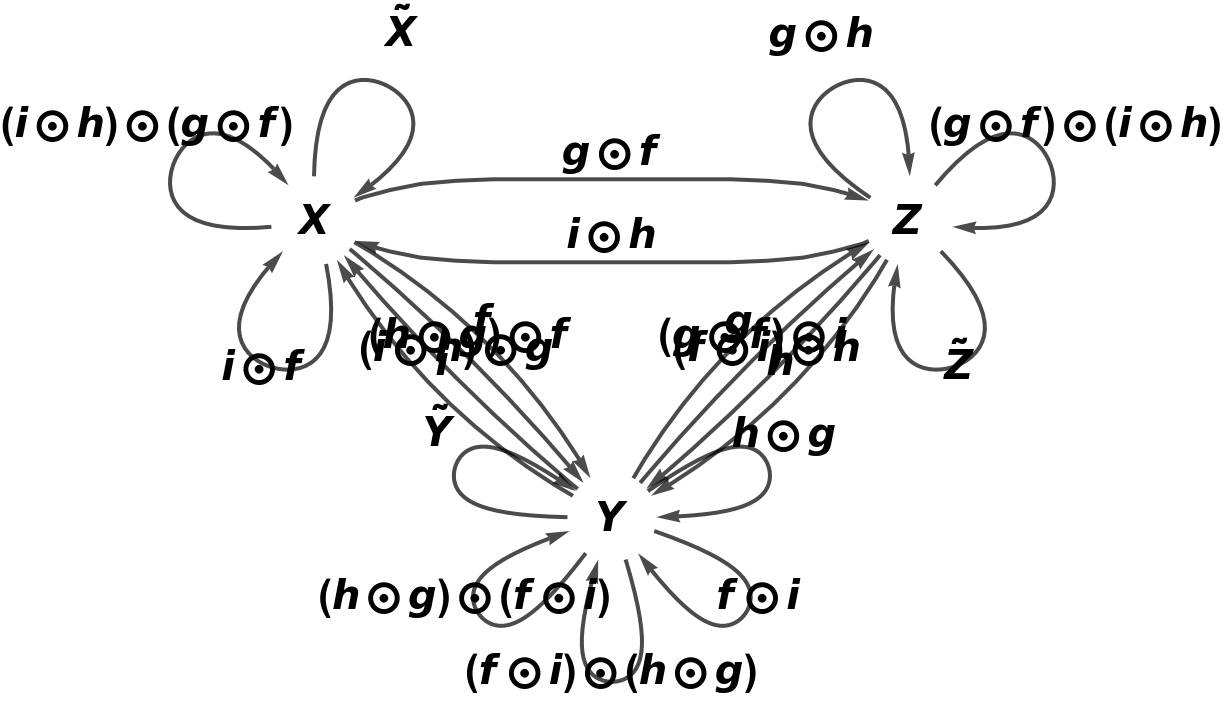
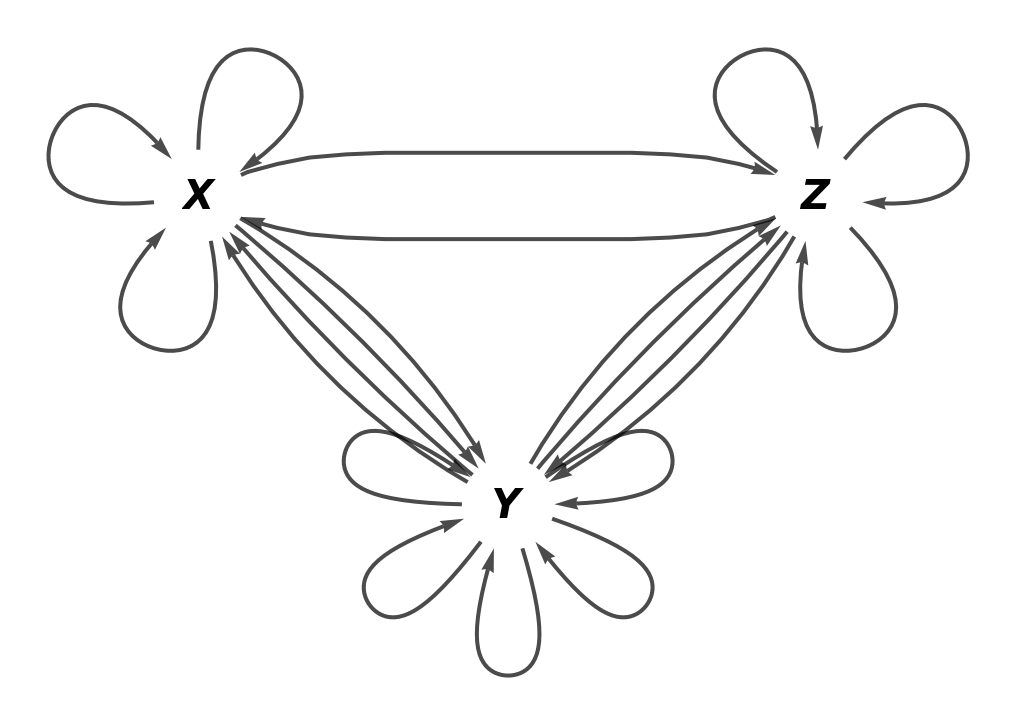
Construct a new abstract category with two-way arrows between objects X, Y and Z:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show that the category is not a groupoid:
Compute the list of equations between morphisms that must hold for the category to be a groupoid:
Show the associations of endomorphisms (morphisms from an object to itself) and automorphisms (isomorphisms from an object to itself):
Construct an abstract category consisting of exactly one morphism from object X to every morphism in the category, together with a single morphism to X, modulo all equivalences between morphisms:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
Show the reduced directed graph without labels on the morphisms:
Show the association of initial objects (i.e. objects with exactly one outgoing morphism to every object):
Show that X is an initial object, modulo all equivalences between morphisms:
Show that X is also a strict initial object (i.e. every incoming morphism to X is an isomorphism) when one mods out by all equivalences between morphisms:
Every initial object is a terminal object (i.e. an object with exactly one incoming morphism to every object) in the dual category:
Likewise with strictly initial objects being strictly terminal objects (i.e. terminal objects for which every outgoing morphism is an isomorphism) in the dual category:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
In both cases, X is not a zero object (i.e. it is not both initial and terminal) nor a strict zero object (i.e. it is not both strictly initial and strictly terminal):
Show, therefore, that the category is not pointed (i.e. it does not contain a zero object):
Construct an abstract category consisting of a pair of parallel morphisms g1 and g2 and a third morphism f leading out from them:
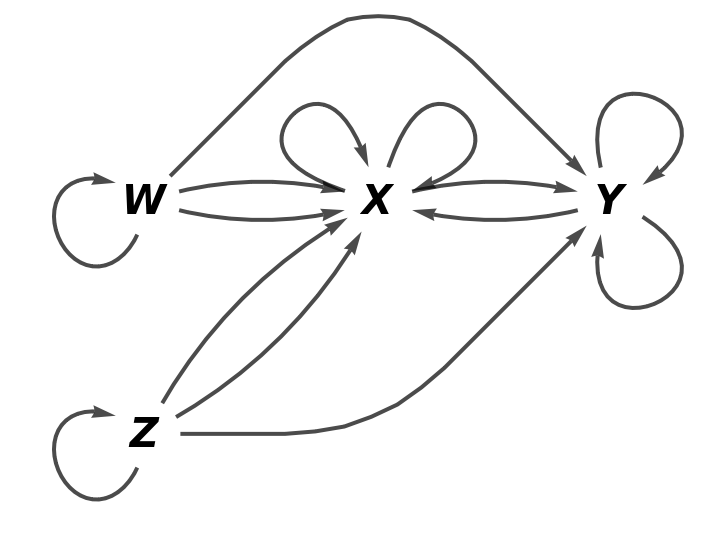
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show that f is not a constant morphism (i.e. does not yield the same result when composed on the right by either member of a parallel pair of morphisms):
Construct the same abstract category, but with an additional equivalence imposed between morphisms f⊙g1 and f⊙g2, thus forcing f to be constant:
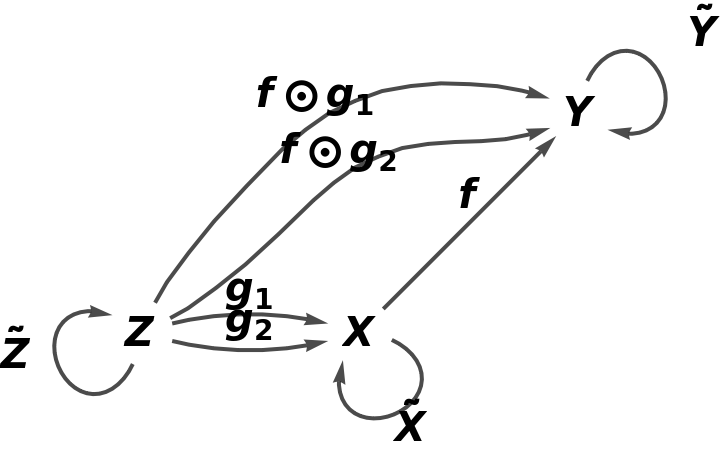
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms:
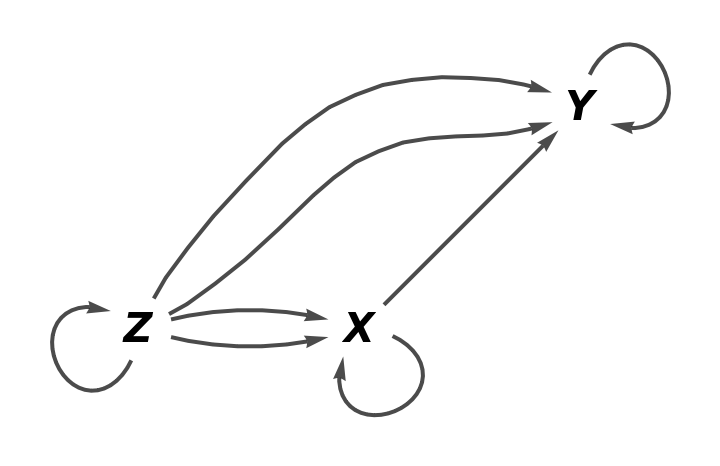
Show the reduced directed graph without labels on the morphisms:
Show that f is now a constant morphism:
Show the association of constant morphisms modulo all equivalences between objects and morphisms:
Every constant morphism is a coconstant morphism (i.e. a morphism that yields the same result when composed on the left by either member of a parallel pair of morphisms) in the dual category:
Show the full directed graph with labels on the morphisms:
Show the full directed graph without labels on the morphisms:
Show the association of zero morphisms (i.e. morphisms that are both constant and coconstant), illustrating that f is also zero:
Show the association of zero morphisms modulo all equivalences between objects and morphisms:
Scope (4)
Abstract categories can be constructed directly from abstract quiver objects (by enforcing the composition and identity axioms on the arrows and objects of the underlying quiver):
Additional arguments can be used to specify the composition and identity symbols:
Alternatively, additional arguments can be used to specify equivalences between objects and morphisms:
All four properties (composition symbol, identity symbol, object equivalences and morphism equivalences) may be specified simultaneously:
Abstract categories can also be constructed directly from directed graph objects (with automatically selected arrow/morphism names):
Similarly, additional arguments can be used to specify composition and identity symbols, as well as equivalences between the resulting objects and morphisms:
Abstract categories can be constructed from lists of arrows (with automatically selected arrow/morphism names):
From associations of arrows/morphisms (with explicitly provided arrow/morphism names):
With explicit lists of objects specified:
Composition and identity symbols can be specified for any abstract category:
Likewise, lists of object equivalences and arrow equivalences can be specified for any abstract category:
New composition and identity symbols can be specified for any existing abstract category:
Likewise for new object and morphism equivalences:
From an explicit association:
Construct an abstract category from an association of arrows/morphisms with additional object and morphism equivalences:
Show the list of properties:
Show the list of objects in the abstract category:
Show the number of objects in the abstract category:
Show the association of morphisms in the abstract category:
Show the list of names of morphisms in the abstract category:
Show the list of directed edges corresponding to morphisms in the abstract category:
Show the number of morphisms in the abstract category:
Show the list of equivalences between objects in the abstract category:
Show the number of equivalences between objects in the abstract category:
Show the list of equivalences between morphisms in the abstract category:
Show the number of equivalences between morphisms in the abstract category:
Show the list of reduced objects (modded out by all object equivalences) in the abstract category:
Show the number of reduced objects (modded out by all object equivalences) in the abstract category:
Show the association of reduced morphisms (modded out by all object and morphism equivalences) in the abstract category:
Show the list of names of reduced morphisms (modded out by all morphism equivalences) in the abstract category:
Show the list of directed edges corresponding to reduced morphisms (modded out by all object and morphism equivalences) in the abstract category:
Show the number of reduced morphisms (modded out by all object and morphism equivalences) in the abstract category:
Show the association of simple morphisms (with all self-loops and multiedges removed) in the abstract category:
Show the list of names of simple morphisms (with all self-loops and multiedges removed) in the abstract category:
Show the list of directed edges corresponding to simple morphisms (with all self-loops and multiedges removed) in the abstract category:
Show the number of simple morphisms (with all self-loops and multiedges removed) in the abstract category:
Show the association of reduced simple morphisms (with all self-loops and multiedges removed, plus all object and morphism equivalences modded out) in the abstract category:
Show the list of names of reduced simple morphisms (with all self-loops and multiedges removed, plus all object and morphism equivalences modded out) in the abstract category:
Show the list of directed edges corresponding to reduced simple morphisms (with all self-loops and multiedges removed, plus all object and morphism equivalences modded out) in the abstract category:
Show the number of reduced simple morphisms (with all self-loops and multiedges removed, plus all object and morphism equivalences modded out) in the abstract category:
Show the (binary) symbol used to denote morphism composition in the abstract category:
Show the (unary) symbol used to denote identity morphisms on objects in the abstract category:
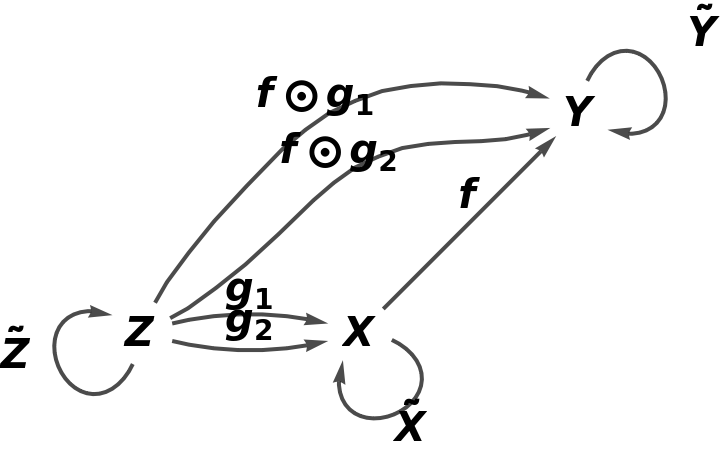
Compute the dual category (obtained by swapping the source and target objects of each morphism and reversing the direction of morphism composition):
Show the abstract quiver forming the underlying structure of the abstract category:
Show the list of equations imposed implicitly by the axiom that morphism composition in the abstract category must be associative:
Show the list of equations imposed implicitly by the axiom that morphism composition in the abstract category must be associative, modulo all equivalences between objects and morphisms:
Show the list of equations imposed implicitly by the axiom that every object in the abstract category must have an identity morphism:
Show the list of equations imposed implicitly by the axiom that every object in the abstract category must have an identity morphism, modulo all equivalences between objects and morphisms:
Determine whether the abstract category is a commutative diagram (i.e. all directed paths through the graph with the same source and target object yield the same morphism):
Show the list of equations between morphisms required to force the abstract category to be a commutative diagram:
Show the list of equations between morphisms required to force the abstract category to be a commutative diagram, modulo all equivalences between objects and morphisms:
Show the association of monomorphisms (i.e. left-cancellative/injective morphisms) in the abstract category:
Show the association of monomorphisms (i.e. left-cancellative/injective morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of epimorphisms (i.e. right-cancellative/surjective morphisms) in the abstract category:
Show the association of epimorphisms (i.e. right-cancellative/surjective morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of bimorphisms (i.e. left- and right-cancellative/bijective morphisms) in the abstract category:
Show the association of bimorphisms (i.e. left- and right-cancellative/bijective morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of retractions (i.e. left inverse morphisms) in the abstract category:
Show the association of retractions (i.e. left inverse morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of left inverse morphisms (i.e. retractions) for each morphism in the abstract category:
Show the association of left inverse morphisms (i.e. retractions) for each morphism in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of sections (i.e. right inverse morphisms) in the abstract category:
Show the association of sections (i.e. right inverse morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of right inverse morphisms (i.e. sections) for each morphism in the abstract category:
Show the association of right inverse morphisms (i.e. sections) for each morphism in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of isomorphisms (i.e. left and right inverse morphisms) in the abstract category:
Show the association of isomorphisms (i.e. left and right inverse morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of inverse morphisms (i.e. isomorphisms) for each morphism in the abstract category:
Show the association of inverse morphisms (i.e. isomorphisms) for each morphism in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of endomorphisms (i.e. morphisms from an object to itself) in the abstract category:
Show the association of endomorphisms (i.e. morphisms from an object to itself) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of automorphisms (i.e. isomorphisms from an object to itself) in the abstract category:
Show the association of automorphisms (i.e. isomorphisms from an object to itself) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of initial objects (i.e. objects with exactly one outgoing morphism to each object) in the abstract category:
Show the association of initial objects (i.e. objects with exactly one outgoing morphism to each object) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of strict initial objects (i.e. initial objects whose incoming morphisms are all isomorphisms) in the abstract category:
Show the association of strict initial objects (i.e. initial objects whose incoming morphisms are all isomorphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of terminal objects (i.e. objects with exactly one incoming morphism from each object) in the abstract category:
Show the association of terminal objects (i.e. objects with exactly one incoming morphism from each object) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of strict terminal objects (i.e. terminal objects whose outgoing morphisms are all isomorphisms) in the abstract category:
Show the association of strict terminal objects (i.e. terminal objects whose outgoing morphisms are all isomorphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of zero objects (i.e. objects with exactly one outgoing morphism and one incoming morphism to/from each object) in the abstract category:
Show the association of zero objects (i.e. objects with exactly one outgoing morphism and one incoming morphism to/from each object) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of strict zero objects (i.e. zero objects whose incoming and outgoing morphisms are all isomorphisms) in the abstract category:
Show the association of strict zero objects (i.e. zero objects whose incoming and outgoing morphisms are all isomorphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Determine whether the abstract category is pointed (i.e. contains a zero object):
Show the association of constant morphisms (i.e. morphisms that yield the same result when composed on the right with either member of a parallel pair of morphisms) in the abstract category:
Show the association of constant morphisms (i.e. morphisms that yield the same result when composed on the right with either member of a parallel pair of morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of coconstant morphisms (i.e. morphisms that yield the same result when composed on the left with either member of a parallel pair of morphisms) in the abstract category:
Show the association of coconstant morphisms (i.e. morphisms that yield the same result when composed on the left with either member of a parallel pair of morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Show the association of zero morphisms (i.e. morphisms that yield the same result when composed on the left or right with either member of a parallel pair of morphisms) in the abstract category:
Show the association of zero morphisms (i.e. morphisms that yield the same result when composed on the left or right with either member of a parallel pair of morphisms) in the abstract category, modulo all equivalences between objects and morphisms:
Determine whether the abstract category is discrete (i.e. all morphisms are identity morphisms):
Determine whether the abstract category is indiscrete (i.e. there exists a unique morphism between every pair of objects):
Determine whether the abstract category is balanced (i.e. every bimorphism is also an isomorphism):
Determine whether the abstract category is a groupoid (i.e. all morphisms are isomorphisms):
Show the list of equations between morphisms required to force the abstract category to be a groupoid (may not necessarily exist):
Show the list of equations between morphisms required to force the abstract category to be a groupoid, modulo all equivalences between objects and morphisms (may not necessarily exist):
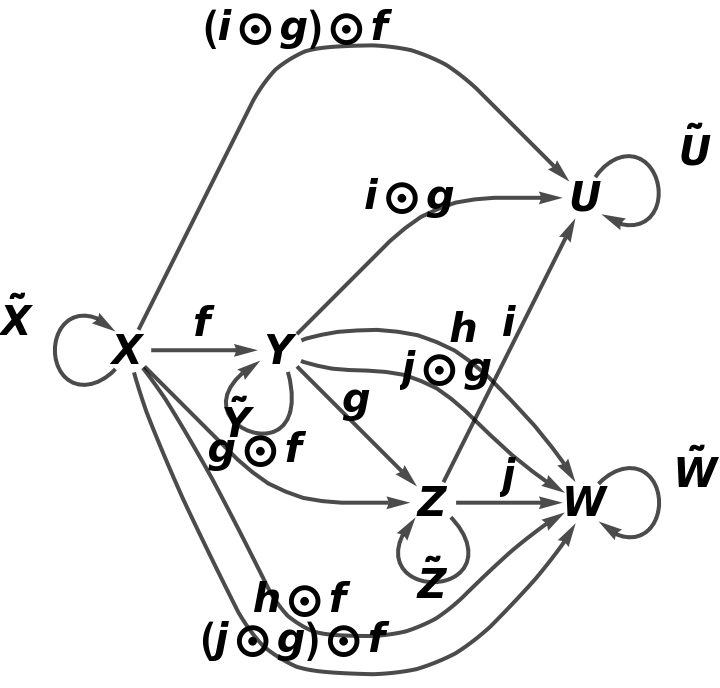
Show the full directed graph with labels on the morphisms of the abstract category:
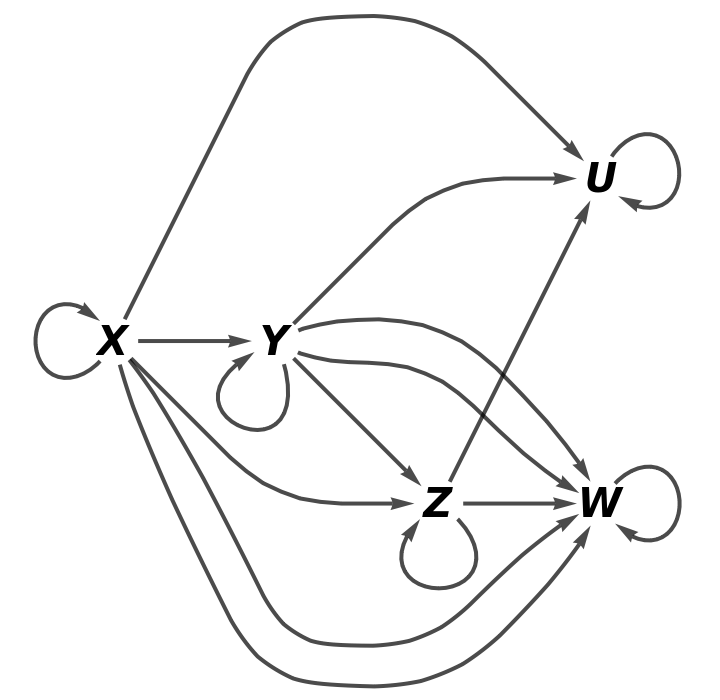
Show the full directed graph without labels on the morphisms of the abstract category:
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and with labels on the morphisms of the abstract category:
Show the reduced directed graph, with all equivalences between objects and morphisms imposed and without labels on the morphisms of the abstract category:
Show the simple directed graph, with all self-loops and multiedges removed and with labels on the morphisms of the abstract category:
Show the simple directed graph, with all self-loops and multiedges removed and without labels on the morphisms of the abstract category:
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and with labels on the morphisms of the abstract category:
Show the reduced simple directed graph, with all self-loops and multiedges removed, plus all object and morphism equivalences modded out and without labels on the morphisms of the abstract category:
Show the explicit association form of the category:
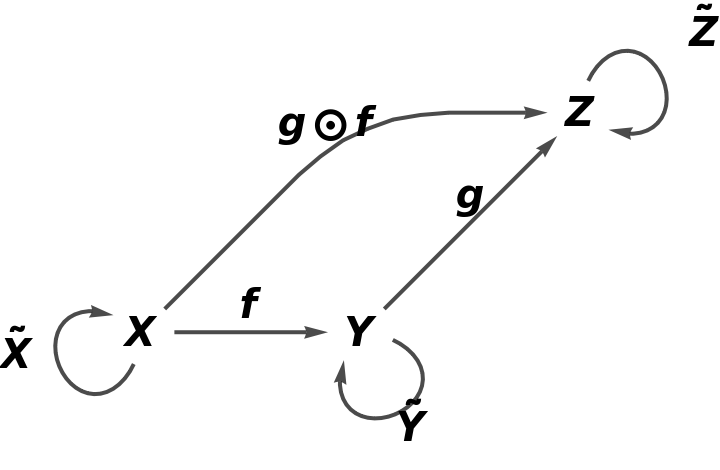
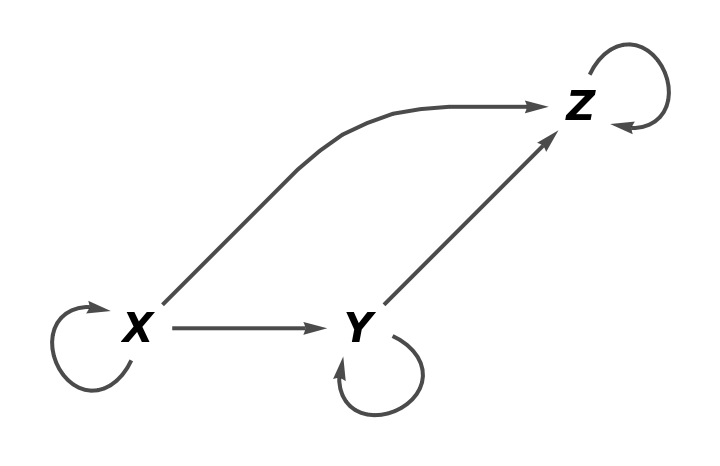
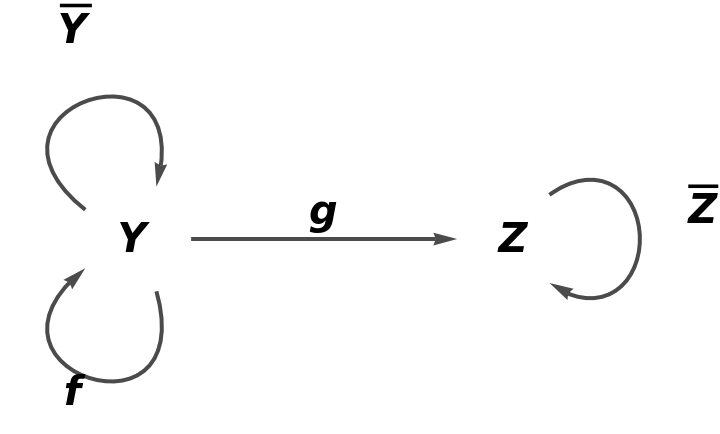
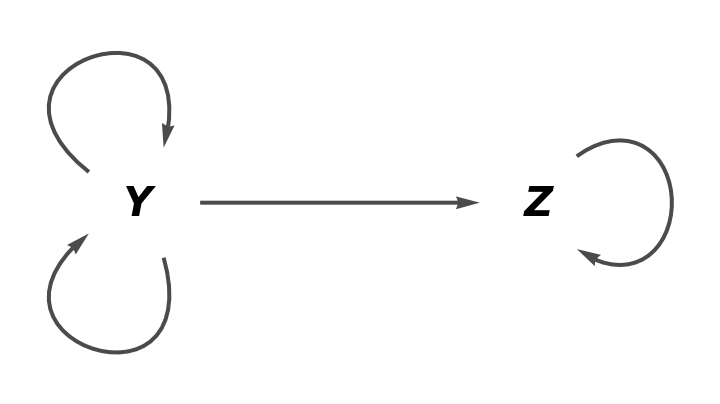

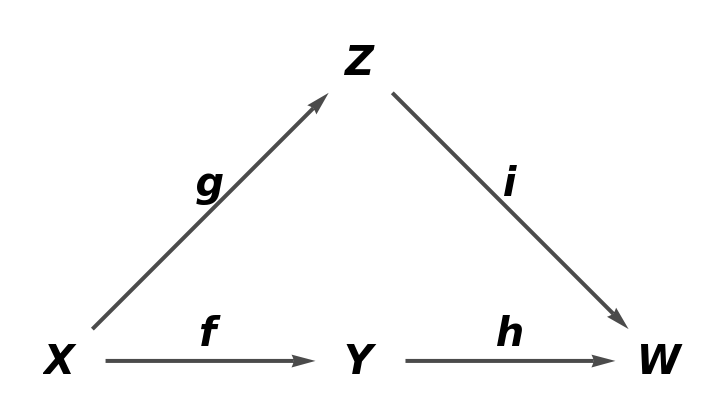
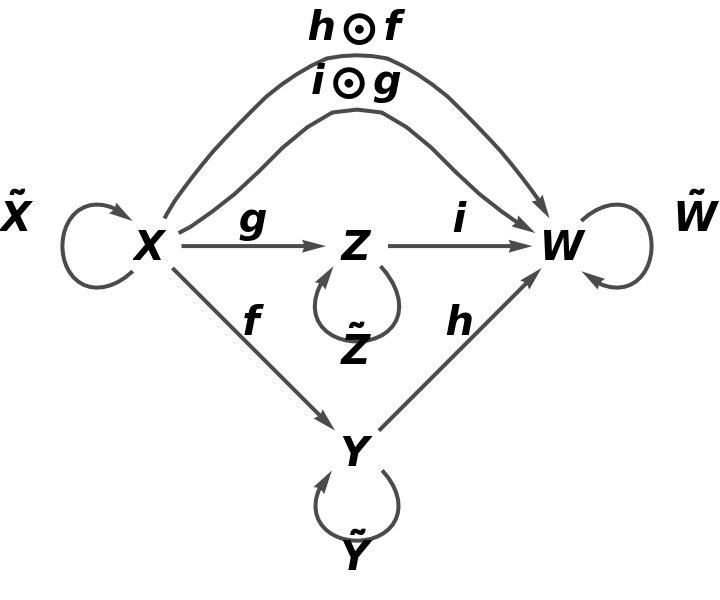
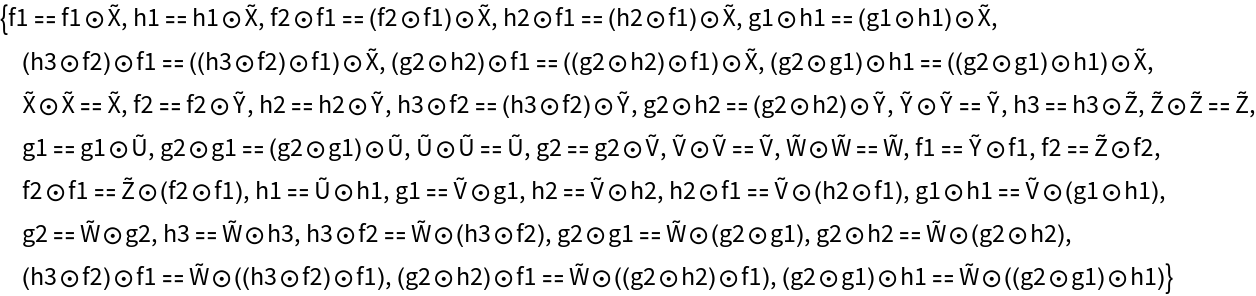


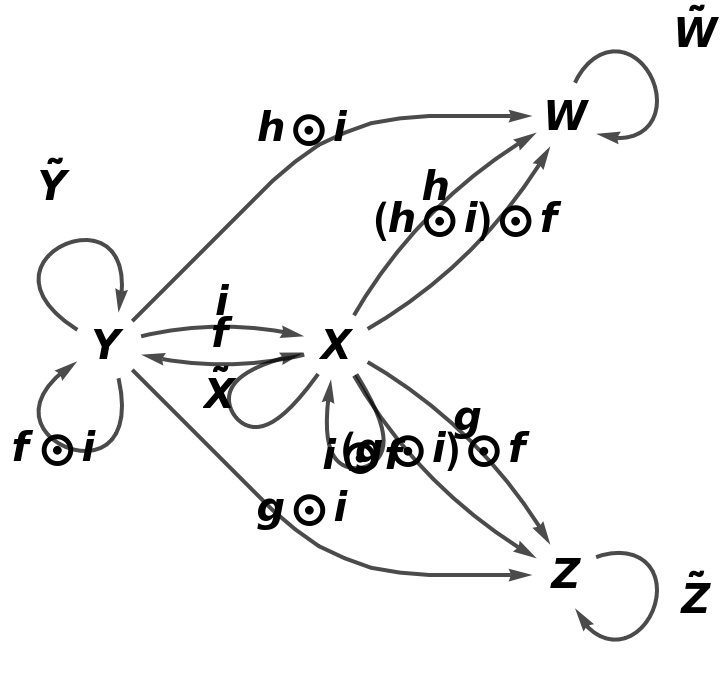
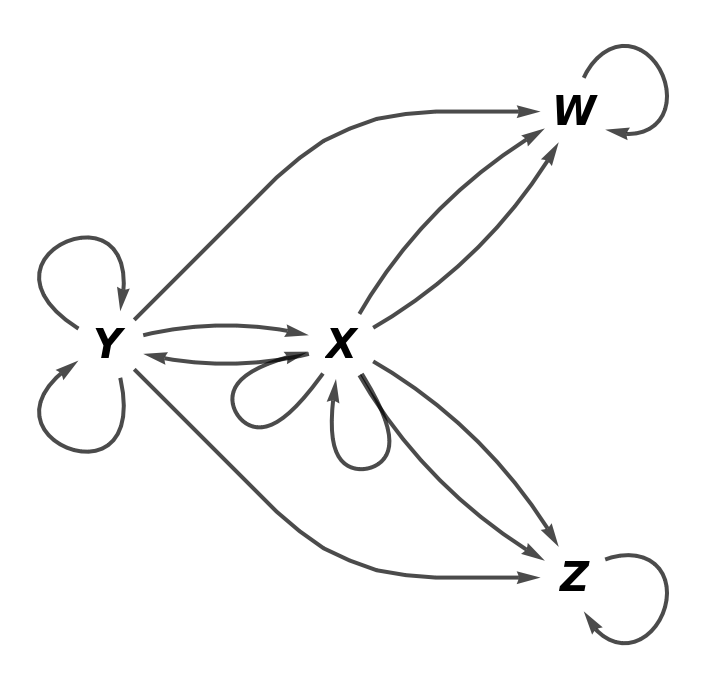
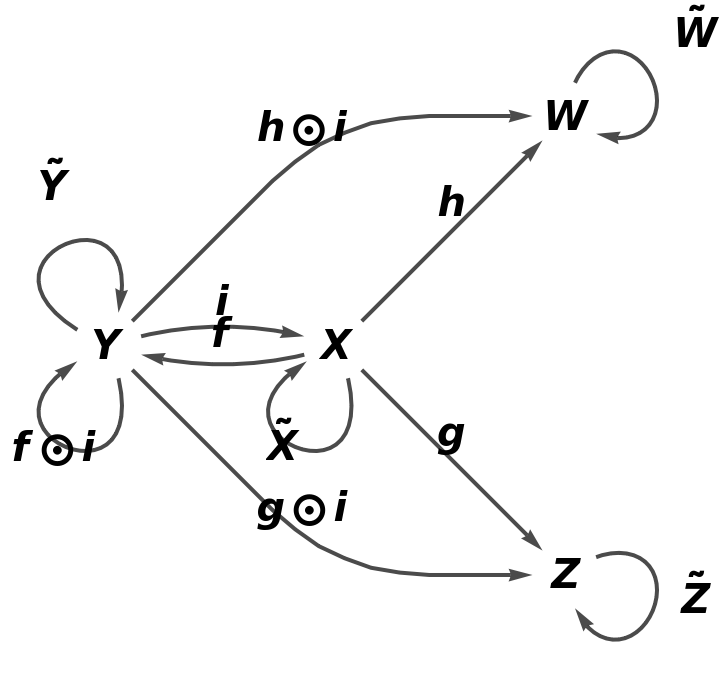
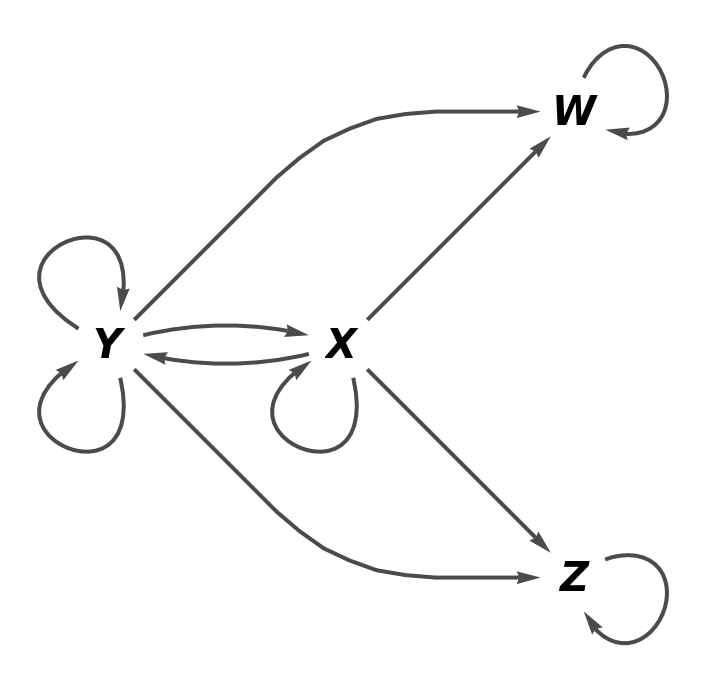
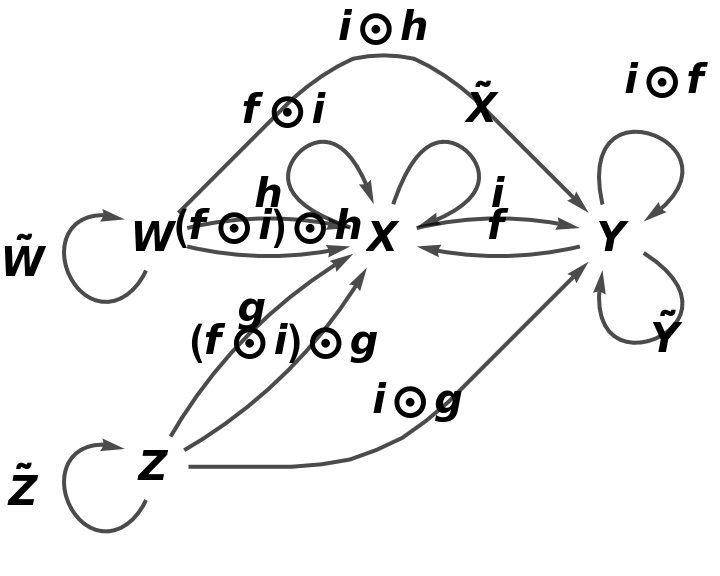
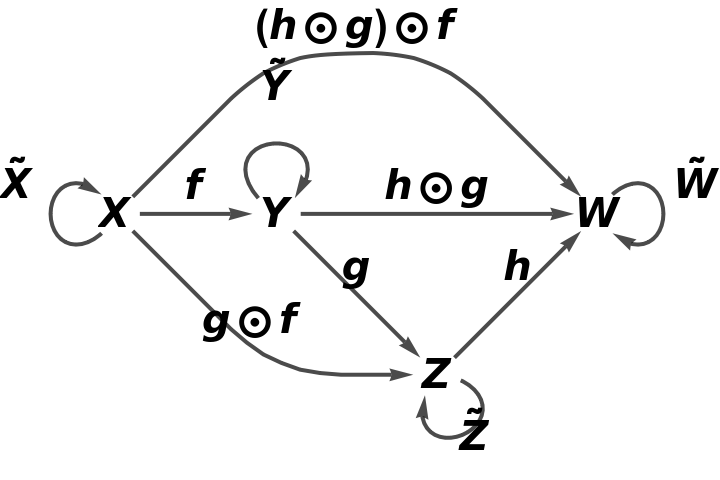
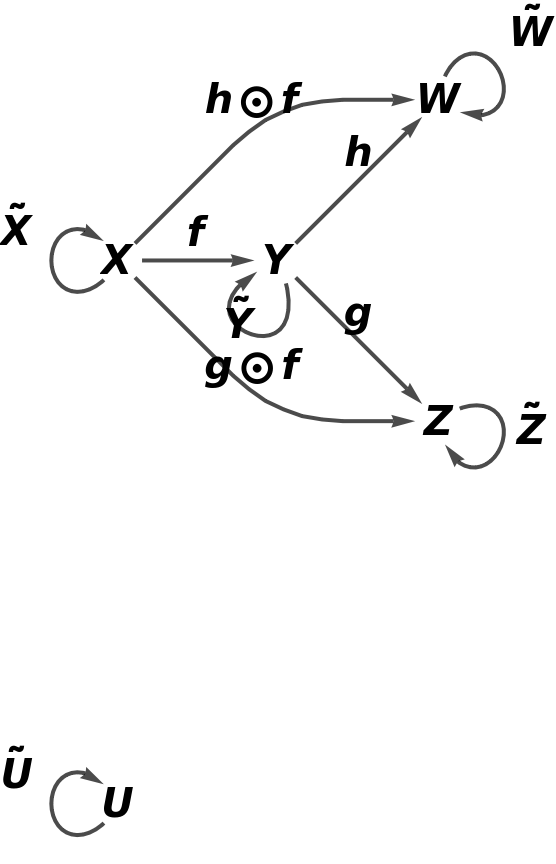
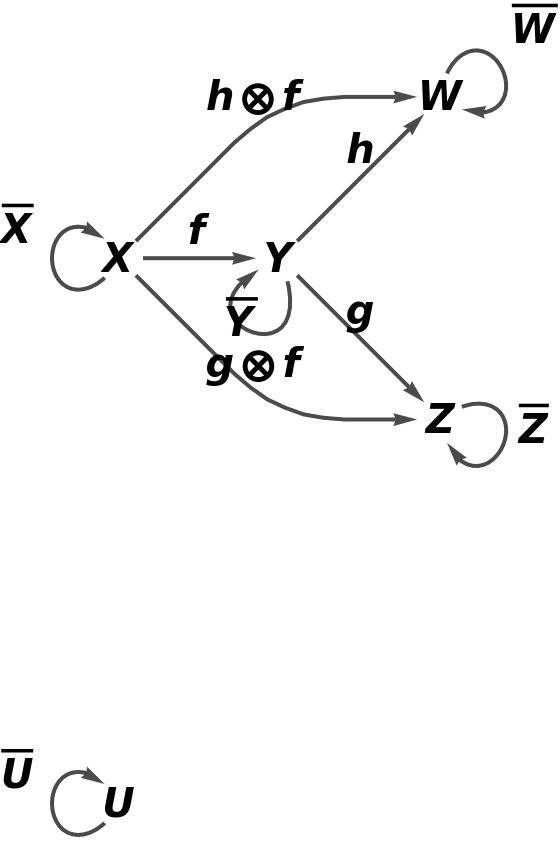
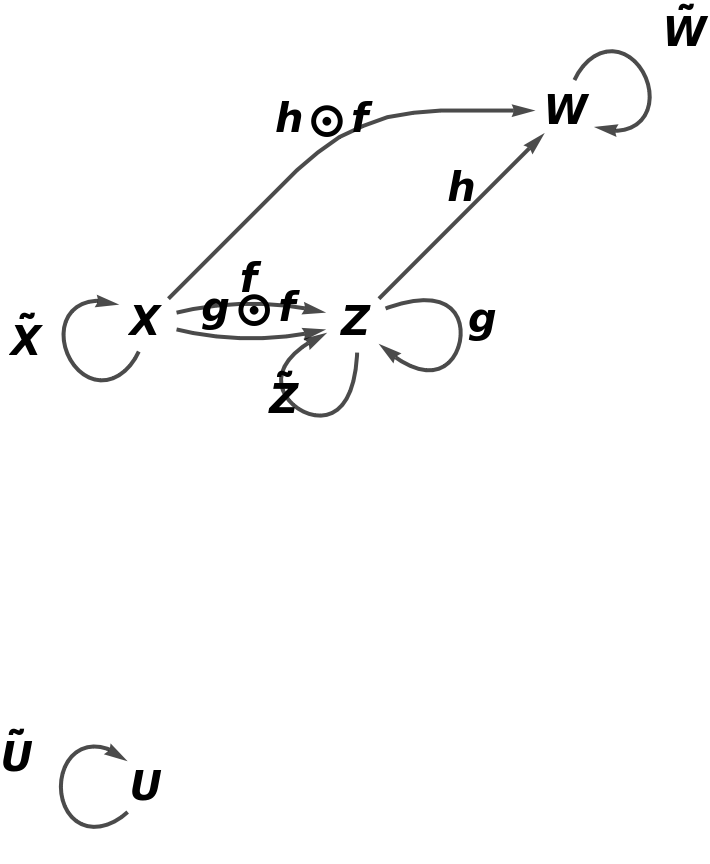
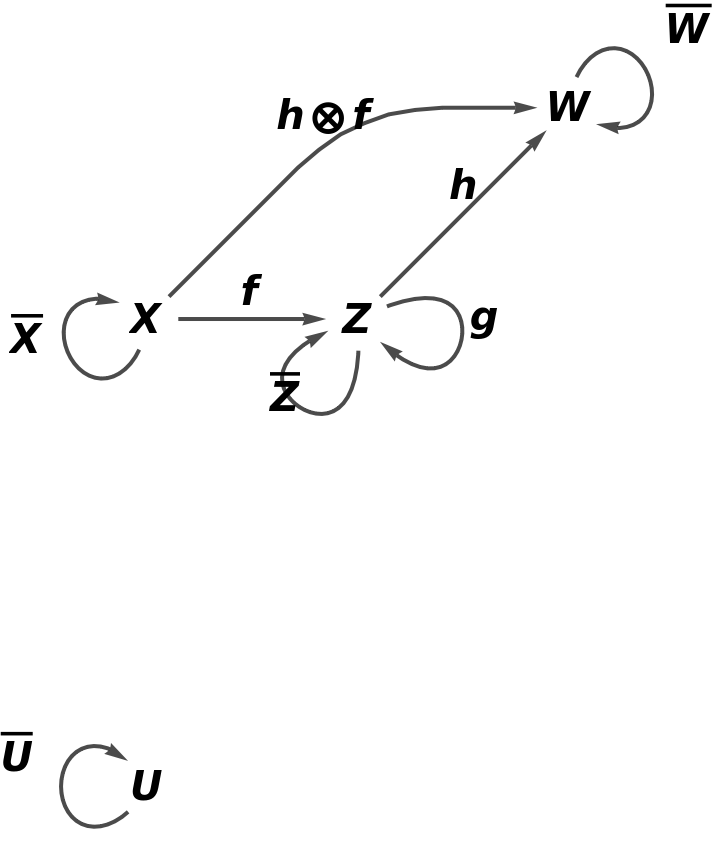
![category8 = ResourceFunction[
"AbstractCategory"][<|"CompositionSymbol" -> CircleDot, "IdentitySymbol" -> OverTilde, "ObjectEquivalences" -> {}, "MorphismEquivalences" -> {}, "Quiver" -> ResourceFunction["AbstractQuiver"][<|f -> {X, Y}, g -> {Y, Z}, h -> {Z, W}|>]|>]](https://www.wolframcloud.com/obj/resourcesystem/images/af7/af7b79f7-7e05-4400-a852-8ca3feb5ddb4/3edbda7bed19c973.png)