Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 InversionCurve

Source Notebook

Compute the inversion of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["InversionCurve"][k,curve,t]

computes the inversion of curve with respect to a circle with radius k and parameter t.

ResourceFunction["InversionCurve"][o,k,curve,t]

computes the inversion of a curve with respect to a circle centered at o.

Details and Options

For a circle C with center O and radius k, if there is a point P in the curve and a point Q in the inverse, then OP·OQ=k2.

Examples

Basic Examples (3) 

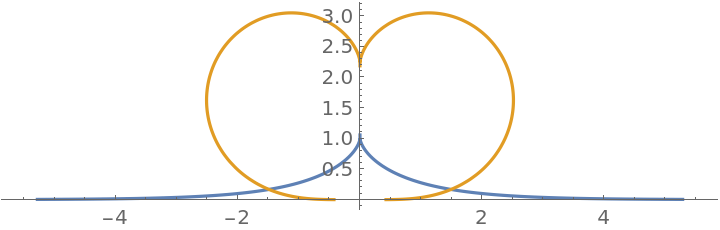
Inversion curve of a tractrix (orange):

In[1]:=
tractrix = Entity["PlaneCurve", "Tractrix"]["ParametricEquations"]
Out[1]=
In[2]:=
ResourceFunction["InversionCurve"][1.5, tractrix[1][t], t]
Out[2]=
In[3]:=
ParametricPlot[ Evaluate[{tractrix[1][t], ResourceFunction["InversionCurve"][1.5, tractrix[1][t], t]}], {t, -2 \[Pi], 2 \[Pi]}]
Out[3]=

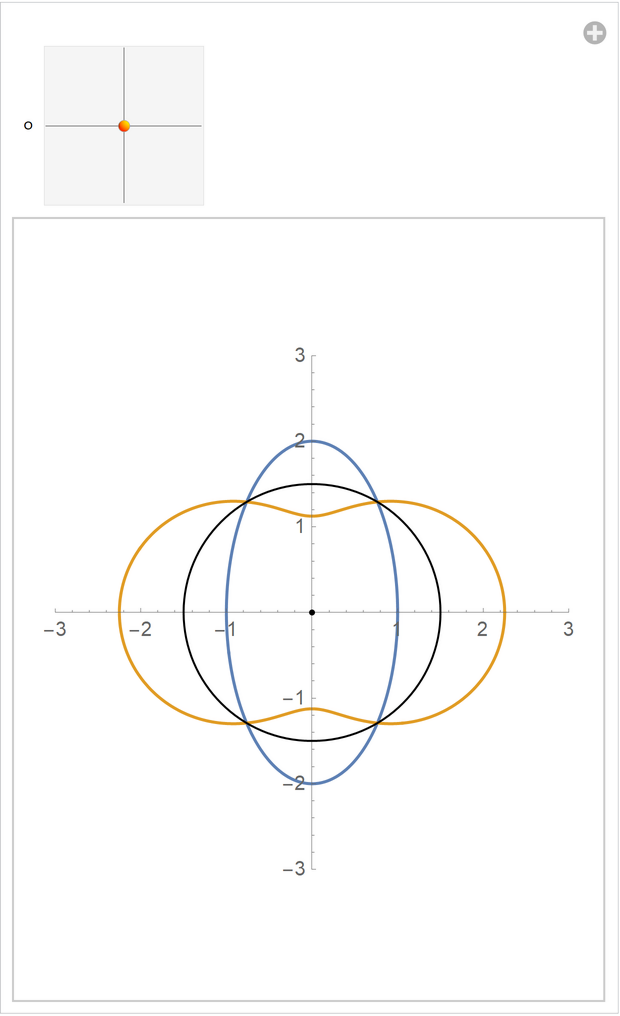
Inversion curve of an ellipse (follows the point and the circle):

In[4]:=
ellipse = Entity["PlaneCurve", "Ellipse"]["ParametricEquations"][1, 2]
Out[4]=
In[5]:=
ResourceFunction["InversionCurve"][{3, 2}, 4, ellipse[t], t]
Out[5]=
In[6]:=
Manipulate[ ParametricPlot[ Evaluate[{ellipse[t], ResourceFunction["InversionCurve"][o, 1.5, ellipse[t], t]}], {t, 0, 2 \[Pi]}, PlotRange -> 3, Epilog -> {Point[o], Circle[o, 1.5]}], {{o, {0, 0}}, {-3, -3}, {3, 3}}]
Out[6]=

A clothoid:

In[7]:=
clothoidprime[n_,a_][t_]:= a{Sin[t^(n+1)/(n+1)], Cos[t^(n+1)/(n+1)]} clothoid[n_,a_][t_]:= Integrate[clothoidprime[n,a][tt], {tt,0,t}]

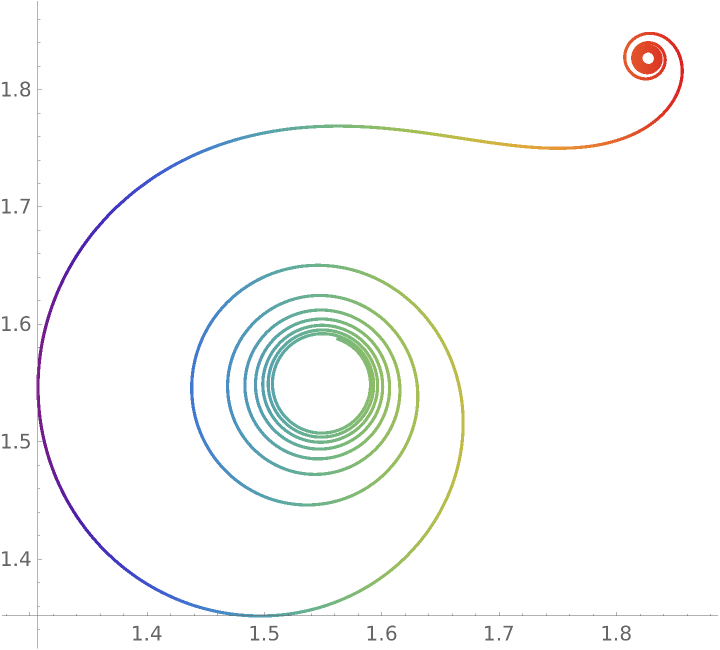
Inversion of a clothoid:

In[8]:=
ResourceFunction["InversionCurve"][{2, 2}, 1, clothoid[1, 1][t], t]
Out[8]=
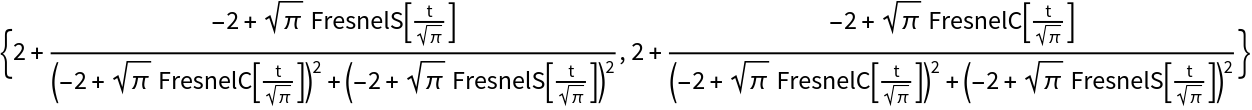
In[9]:=
ParametricPlot[ Evaluate[ResourceFunction["InversionCurve"][{2, 2}, 1, clothoid[1, 1][t], t]], {t, -10, 10}, ColorFunction -> "Rainbow"]
Out[9]=

A helicoid:

In[10]:=
helix[a_, b_][t_] := {a Cos[t], a Sin[t], b t}

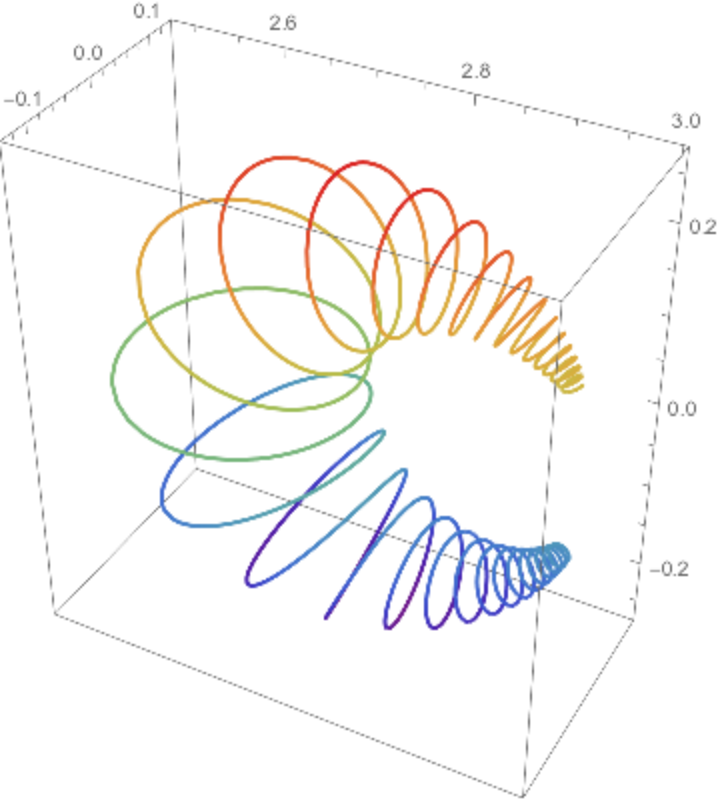
Inversion of a helix:

In[11]:=
ResourceFunction["InversionCurve"][{3, 0, 0}, 1, helix[1, 1/10][t], t]
Out[11]=
In[12]:=
ParametricPlot3D[%, {t, -30 \[Pi], 30 \[Pi]}, PlotPoints -> 1500, Boxed -> True, PlotRange -> All, ColorFunction -> "Rainbow"]
Out[12]=

Possible Issues (1) 

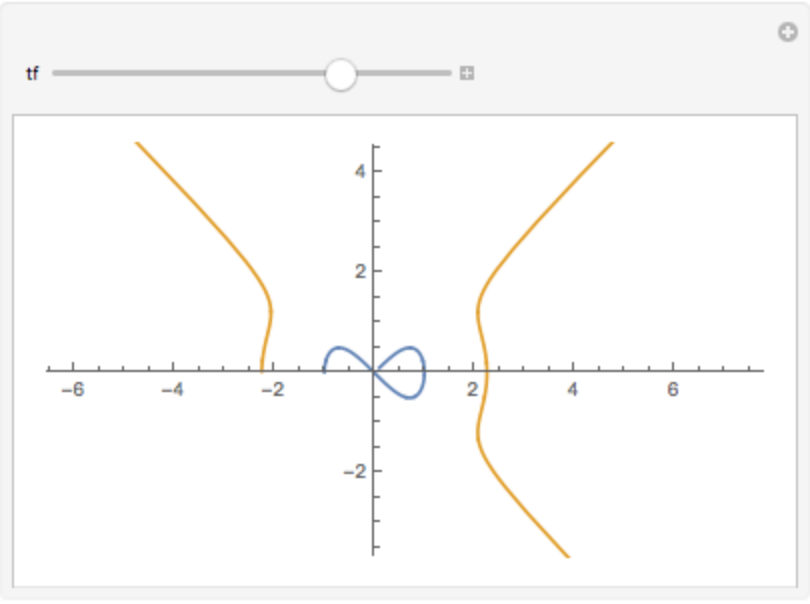
Avoid division by zero:

In[13]:=
eight[t_] := {Sin[t], Sin[t] Cos[t]}
In[14]:=
ResourceFunction["InversionCurve"][3, eight[t], t]
Out[14]=
In[15]:=
Manipulate[ ParametricPlot[ Evaluate[{eight[t], ResourceFunction["InversionCurve"][3/2, eight[t], t]}], {t, 0.1, tf}, Exclusions -> {\[Pi]}, ExclusionsStyle -> None], {{tf, 4.7}, 0.01, 2 \[Pi]}]
Out[15]=

Publisher

Enrique Zeleny

Version History

  • 2.0.0 – 31 August 2020
  • 1.0.0 – 24 February 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information