Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 PolynomialHermiteDecomposition

Source Notebook

Compute the Hermite decomposition of a matrix of univariate polynomials

Contributed by: Daniel Lichtblau

ResourceFunction["PolynomialHermiteDecomposition"][mat]

computes the Hermite decomposition of the matrix mat of univariate polynomials.

ResourceFunction["PolynomialHermiteDecomposition"][mat,x]

computes the Hermite decomposition for a matrix of polynomials in the variable x.

Details and Options

The result is given in the form {u,h} where u is a unimodular matrix, h is an upper‐triangular matrix, and u.mat⩵h.
The Hermite form matrix will have zeros below all pivot elements, and polynomials above a given pivot will have lower degree than that pivot.
A unimodular matrix over a ring of univariate polynomials is a matrix with nonzero determinant lying in the coefficient field (that is, a constant).
The Hermite form is similar to the reduced echelon form, except divisions in the polynomial field are not permitted. Rather than using division to “normalize” pivots to unity, pivot degrees are reduced using the extended polynomial GCD operation on pairs of elements in a given matrix column.
Multivariate polynomials are regarded as univariate in the specified variable, with all others treated as symbolic coefficients.
ResourceFunction["PolynomialHermiteDecomposition"] takes Method and Modulus as options.
ResourceFunction["PolynomialHermiteDecomposition"] is intended for matrices of polynomials in a single variable, with all coefficients either exact or approximate numbers.

Examples

Basic Examples (3) 

Compute the Hermite decomposition of a 2×3 matrix of low-degree polynomials:

In[1]:=
mat = {{x^3 - 11, x^2 - 2*x + 5, x^3 - 2*x^2 + 3*x - 7}, {x^2 + 4*x + 9, x^2 - 19, x^3 + 5*x - 6}}; {u, h} = ResourceFunction["PolynomialHermiteDecomposition"][mat]
Out[2]=

Check the matrix equation:

In[3]:=
Expand[u . mat - h]
Out[3]=

Check that u is unimodular:

In[4]:=
Det[u]
Out[4]=

Options (6) 

Generate and compute the Hermite decomposition for an 8×12 matrix of random degree-5 polynomials with coefficients between −10 and 10:

In[5]:=
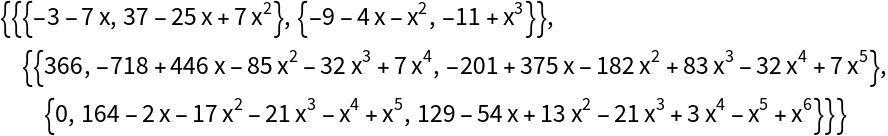
randomPoly[deg_, max_, x_] := RandomInteger[{-max, max}, deg + 1] . x^Range[0, deg] randomMatrix[m_, n_, deg_, max_, x_] := Table[randomPoly[deg, max, x], {m}, {n}] SeedRandom[1111]; bigmat = randomMatrix[8, 12, 5, 10, x]; Timing[{u, h} = ResourceFunction["PolynomialHermiteDecomposition"][bigmat];]
Out[6]=

Computing this by the direct method is comparatively slower:

In[7]:=
Timing[{u2, h2} = ResourceFunction["PolynomialHermiteDecomposition"][bigmat, Method -> "Direct"];]
Out[7]=

The situation is typically reversed when one works over a prime field (this is reflected in the Automatic method selection):

In[8]:=
Timing[{umod, hmod} = ResourceFunction["PolynomialHermiteDecomposition"][bigmat, Modulus -> 103, Method -> "GroebnerBasis"];]
Out[8]=
In[9]:=
Timing[{umod2, hmod2} = ResourceFunction["PolynomialHermiteDecomposition"][bigmat, Modulus -> 103, Method -> "Direct"];]
Out[9]=

Also, the direct method is typically more reliable than the one that uses a Gröbner basis computation:

In[10]:=
Timing[{ufprec, hfprec} = ResourceFunction["PolynomialHermiteDecomposition"][N[bigmat, 100], Method -> "Direct"];]
Out[10]=

The Gröbner basis method needs to have higher precision input for this example:

In[11]:=
Timing[{ufprec2, hfprec2} = ResourceFunction["PolynomialHermiteDecomposition"][N[bigmat, 100], Method -> "GroebnerBasis"];]
Out[11]=
In[12]:=
Timing[{ufprec2, hfprec2} = ResourceFunction["PolynomialHermiteDecomposition"][N[bigmat, 300], Method -> "GroebnerBasis"];]
Out[12]=

The results agree:

In[13]:=
N[{ufprec - ufprec2, hfprec - hfprec2}]
Out[13]=

Applications (7) 

Polynomial solutions to polynomial systems (7) 

If a polynomial solution exists, it can be found using the Hermite decomposition:

In[14]:=
solvePolynomialSystem[mat_, rhs_, x_] := Module[ {tmat = Join[{rhs}, Transpose[mat]], augmat, uu, hh, soln, len = Length[rhs]}, augmat = Join[tmat, IdentityMatrix[Length[tmat]], 2]; {uu, hh} = ResourceFunction["PolynomialHermiteDecomposition"][augmat, x]; soln = SelectFirst[hh, (#[[len + 1]] =!= 0 && FreeQ[#[[len + 1]], x]) &, "Missing"]; If[soln === "Missing", {}, -Drop[soln, len + 1]/soln[[len + 1]]] ]

Create an underdetermined system using an 8×12 matrix of random degree-5 polynomials with coefficients between -10 and 10, and an eight-dimensional right-hand-side polynomial of the same specification:

In[15]:=
randomPoly[deg_, max_, x_] := RandomInteger[{-max, max}, deg + 1] . x^Range[0, deg] randomMatrix[m_, n_, deg_, max_, x_] := Table[randomPoly[deg, max, x], {m}, {n}] SeedRandom[1111]; bigmat = randomMatrix[8, 12, 5, 10, x]; bigrhs = Flatten[randomMatrix[8, 1, 5, 10, x]];

Solve this system:

In[16]:=
Timing[soln = solvePolynomialSystem[bigmat, bigrhs, x];]
Out[16]=

Check the solution:

In[17]:=
Expand[bigmat . soln - bigrhs]
Out[17]=

Note that some components have high degree:

In[18]:=
Map[Exponent[#, x] &, soln]
Out[18]=

You can get a solution to the system much faster using LinearSolve:

In[19]:=
Timing[soln2 = LinearSolve[bigmat, bigrhs];]
Out[19]=

But several components are rational functions rather than polynomials:

In[20]:=
Map[PolynomialQ[#, x] &, soln2]
Out[20]=

Version History

  • 1.0.0 – 08 November 2019

Related Resources

Author Notes

When input involves approximate numbers in the polynomial coefficients, no attempt is made to find a "perturbed" system that might give a less trivial decomposition (where "trivial" is measured by earlier pivot elements in the Hermite form matrix having higher degree than that of the actual result). This is an area of active research in recent literature.

License Information