Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Define a continuous probability distribution characterized by a Gaussian core and a power-law tail
ResourceFunction["CrystalBallDistribution"][α,n,x_,σ] computes the Crystal Ball distribution for the given shape parameters. |
Symbolic representation of the Crystal Ball distribution:
| In[1]:= |
| Out[1]= | 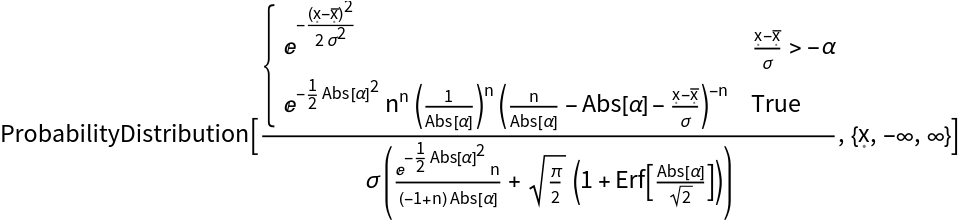 |
Compute the PDF for certain specific parameters:
| In[2]:= |
| Out[2]= | 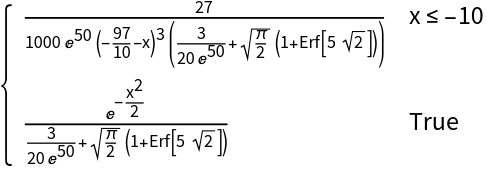 |
| In[3]:= |
| Out[3]= | 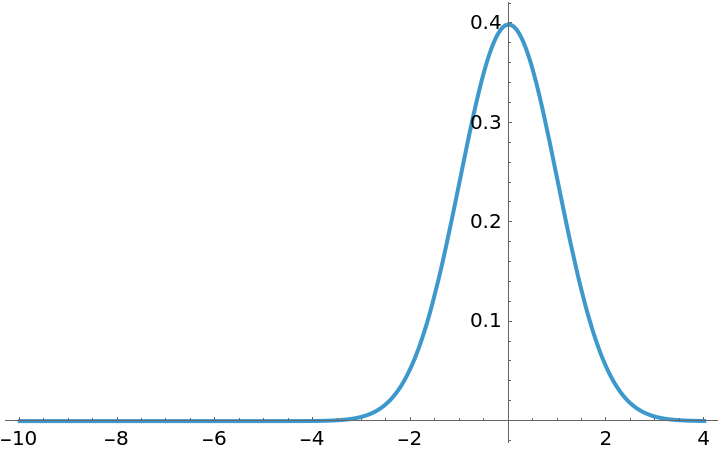 |
Compute the CDF:
| In[4]:= |
| Out[4]= | 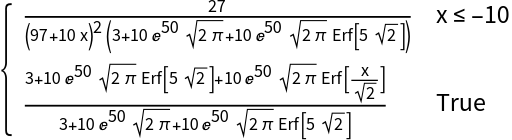 |
Plot the CDF:
| In[5]:= |
| Out[5]= | 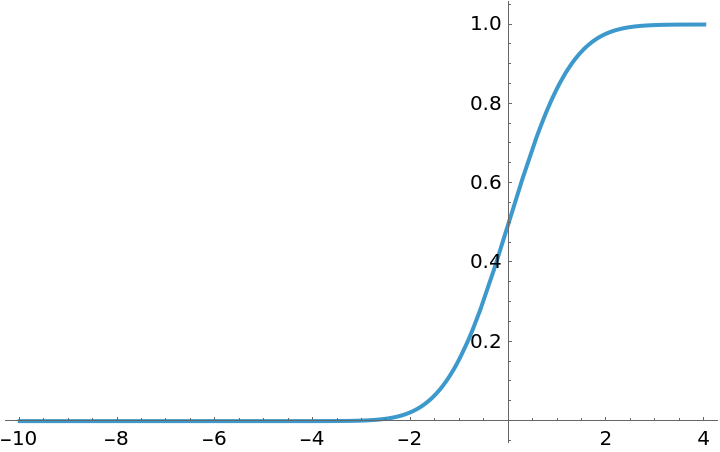 |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License