Function Repository Resource:

LloydAlgorithm

Source Notebook

Perform Lloyd's algorithm to find evenly spaced points in a region

Contributed by: Sander Huisman

ResourceFunction["LloydAlgorithm"][pts, {{x_min,x_max},{y_min,y_max}},n]

performs n iterations of Lloyd's algorithm in a rectangular region.

ResourceFunction["LloydAlgorithm"][pts, reg,n]

performs n iterations of Lloyd's algorithm in the region reg.

Examples

Basic Examples (2)

Perform five iterations of the algorithm on some random points:

In[1]:=

Out[2]=

Spread 15 points evenly in a square box and visualize their neighborhood:

In[3]:=

pts = {{0.7051415661084366, 0.8127461249573649}, {
0.24818358106692706`, 0.7163485756499937}, {0.0025428587961178195`, 0.28314953970466283`}, {0.5733698624847858, 0.9737674379351713}, {
0.22813077794397185`, 0.22547353064271713`}, {0.19238874468210732`, 0.649219075575642}, {0.42688137383256564`, 0.4511465320841044}, {
0.7744365030958476, 0.11274092143618653`}, {0.6724513430791277, 0.8062991370825388}, {0.6677413538921941, 0.37679516587705786`}};
newpts = ResourceFunction["LloydAlgorithm"][pts, {{0, 1}, {0, 1}}, 15];
{Show[{VoronoiMesh[pts], Graphics[Point[pts]]}], Show[{VoronoiMesh[newpts], Graphics[Point[newpts]]}]}

Out[5]=

Scope (2)

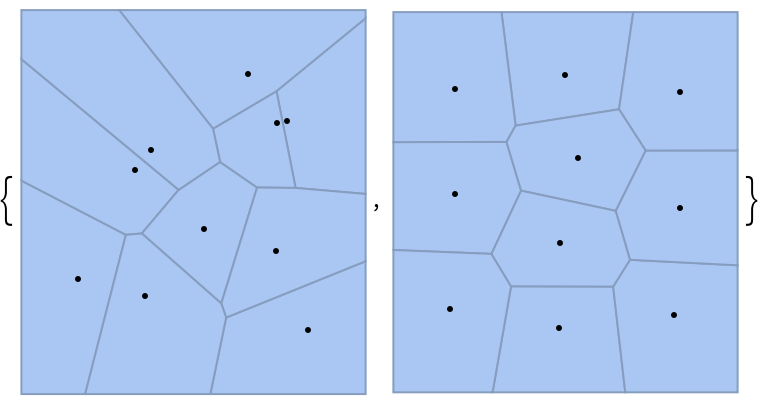Perform 15 iterations in a complicated region:

In[6]:=

SeedRandom[1234];
reg = Disk[{5, 5}, 5];
reg = RegionDifference[reg, Rectangle[{2, 4}, {7, 7}]];
reg = BoundaryDiscretizeRegion[reg];
p = RandomPoint[reg, 20];
p = ResourceFunction["LloydAlgorithm"][p, reg, 15];
Show[{reg, Graphics[{EdgeForm[Black], FaceForm[Gray], Black, Point[p]}]}]

Out[7]=

Perform 15 iterations in a different complicated region:

In[8]:=

$SeedRandom[12345]; reg = ImplicitRegion[x^4 + y^4 + 3 x^3 - 4 y <= 1, {x, y}]; reg = BoundaryDiscretizeRegion[reg]; p = RandomPoint[reg, 20]; p = ResourceFunction["LloydAlgorithm"][p, reg, 10]; Show[{reg, Graphics[Point[p]]}]$

Out[13]=

Neat Examples (2)

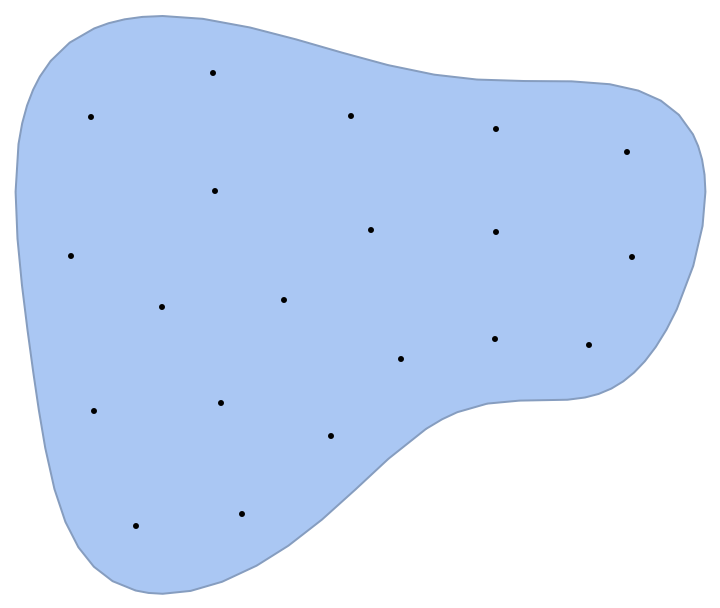See how the standard deviation of the Voronoi areas changes with iterations:

In[14]:=

SeedRandom[1];
bb = {{0, 1}, {0, 1}};
pts = RandomReal[{0, 1}, {10, 2}];
pts = NestList[ResourceFunction["LloydAlgorithm"][#, bb, 1] &, pts, 15];
s = StandardDeviation[
Area /@ MeshPrimitives[VoronoiMesh[#, bb], 2]] & /@ pts;
ListPlot[s, PlotRange -> All]

Out[15]=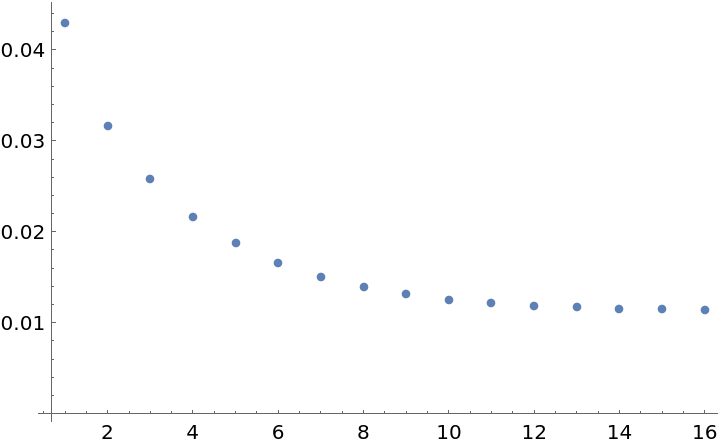

Visualize the evolution:

In[16]:=

Out[16]=

Publisher

SHuisman

Version History

1.0.0 – 06 April 2020

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License