Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 AdaptiveCellularAutomaton

Source Notebook

Run an adaptive search for cellular automata

Contributed by: Willem Nielsen

ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth"→3|>]

returns three steps in an adaptive search, starting from the 3-color null rule and searching for rules that give longer finite length patterns.

ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth"→3, "Rule"→{0,k,r}|>]

returns three steps in an adaptive search, starting from the k-color null rule and searching for rules that give longer finite length patterns.

ResourceFunction["AdaptiveCellularAutomaton"][evospec,"Final"]

returns only the final step in the search.

ResourceFunction["AdaptiveCellularAutomaton"][evospec,"Breakthroughs"]

returns the breakthrough steps in the search.

ResourceFunction["AdaptiveCellularAutomaton"][evospec,sequencespec,"Plot"]

returns the plotted cellular automata for each step specified by the sequence specification.

ResourceFunction["AdaptiveCellularAutomaton"][evospec,sequencespec,"Fitness"]

returns only the fitness values.

ResourceFunction["AdaptiveCellularAutomaton"][evospec,sequencespec,propertyspec]

returns all the information specified by the property specification.

Details

The sequencespec accepts "Finals", "Breakthroughs" or All. All includes all steps in the output.
The following keys can be used for the evolution specification:
"Rule"{0, 3, 1}the initial rule, and the color-space and radius to use
"InitialCondition"{{1}, 0}the initial condition
"Cut"100the number of steps to search to determine if the rule halts
"Depth"1the number of iterations to do in the search
"MutationFunction"1the type and number of mutations to do
"FitnessFunction""Lifetime"the fitness function to use
"SelectionFunction"#1>=#2&the selection function to use
The fitness function specification can have the following values:
"Lifetime"evolve to a longer finite lifetime
"Width"evolve to a wider pattern that still halts
"AspectRatio"evolve to a larger aspect ratio defined as the width over the lifetime
type→targetevolve to a target value for the given fitness type
funa custom function that takes the rule and initial condition and returns the desired fitness
The mutation function specification can have the following values:
nrandomly mutate a n bits in the rule
"Rule" -> nrandomly mutate n bits in the rule
"InitialCondition" -> nrandomly mutate a single bit in the initial condition
funa custom function that takes the rule and returns the mutated version
<|"Rule"→funrule, "InitialCondition"→funic|>mutates the rule and initial condition using the specified functions

Examples

Basic Examples (3) 

Run a search for 3 steps starting from the null k=3, r=1 rule and return every step in the search:

In[1]:=
ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth" -> 3|>]
Out[1]=

Run a search for 100 steps and only return the final result:

In[2]:=
ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Depth" -> 100|>, "Final"]
Out[2]=

Start from the k=4,r=1 rule:

In[3]:=
ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {0, 4, 1}, "Depth" -> 3|>]
Out[3]=

Scope (11) 

Evolve for 500 steps and plot the breakthrough mutation steps:

In[4]:=
SeedRandom[1110]; ResourceFunction[ "AdaptiveCellularAutomaton"][<| "Depth" -> 500|>, "Breakthroughs", "Plot"]
Out[4]=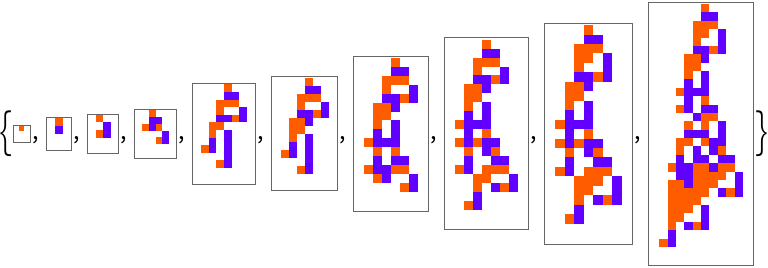

Plot the progressive fitness values showing the mutations that weren't selected:

In[5]:=
SeedRandom[1110]; Show[ListStepPlot[#Fitness & /@ #], ListPlot[#MutatedFitness & /@ #, PlotStyle -> Red]] &[ ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth" -> 500|>, All, {"Fitness", "MutatedFitness"}]]
Out[5]=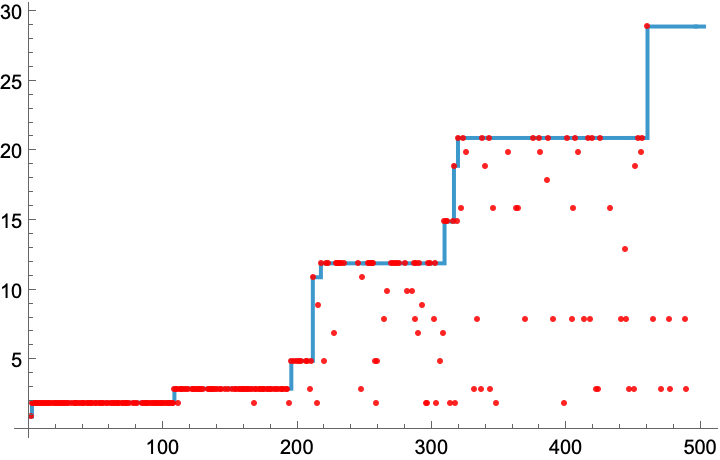

Plot the progressive fitness values for 10 evolutions:

In[6]:=
ListStepPlot[ Table[ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth" -> 500|>, All, "Fitness"], 10], PlotRange -> All]
Out[6]=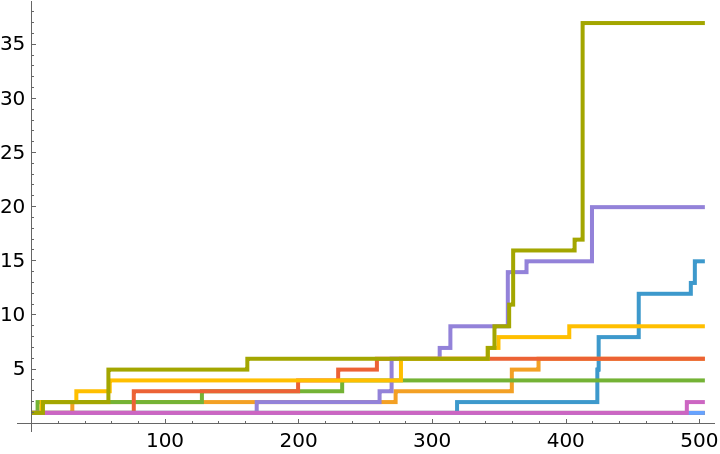

Plot the final states of 10 different evolutions:

In[7]:=
Table[SeedRandom[1110 + i]; ResourceFunction["AdaptiveCellularAutomaton"][<|"Depth" -> 500|>, "Final", "Plot"], {i, 10}]
Out[7]=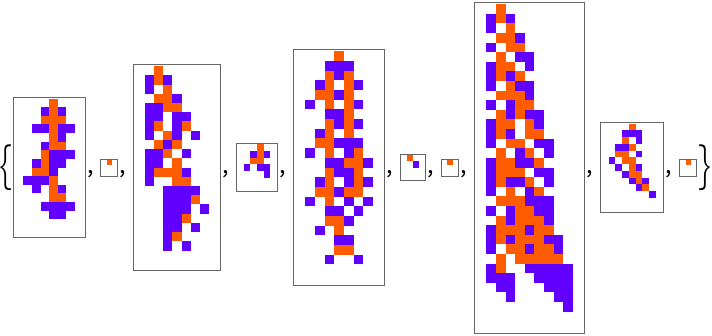

Evolve a k = 4 cellular automata:

In[8]:=
SeedRandom[1112]; ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {0, 4, 1}, "Depth" -> 500|>, "Breakthroughs", "Plot"]
Out[8]=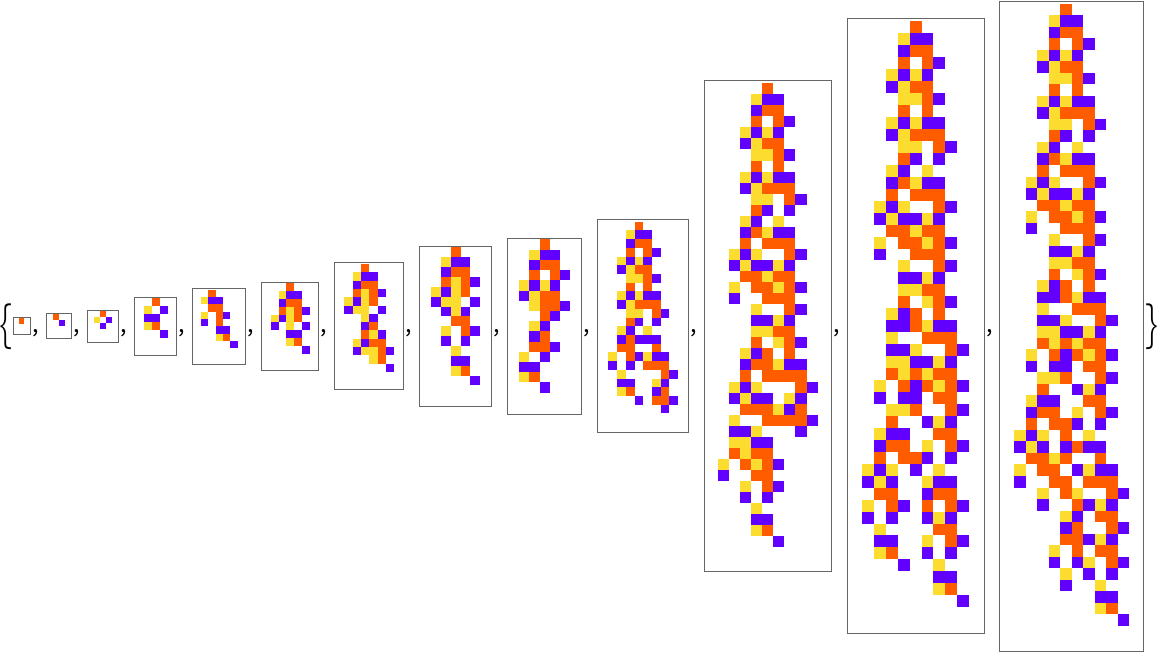

Plot with a length specification:

In[9]:=
SeedRandom[1112]; ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {0, 4, 1}, "Depth" -> 500|>, "Breakthroughs", "Plot" -> {100, {-5, 5}}]
Out[9]=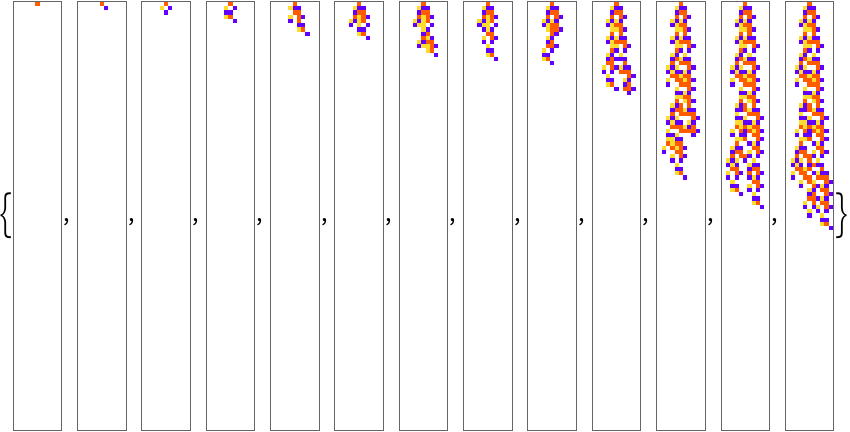

Manually adjust the output function:

In[10]:=
SeedRandom[1112]; ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {0, 4, 1}, "Depth" -> 500|>, "Breakthroughs", (ArrayPlot[ ArrayPad[#, 1] & /@ CellularAutomaton[#Rule, #InitialCondition, #Fitness + 1], ColorRules -> {0 -> GrayLevel[1], 1 -> Hue[0.06, 1, 1], 2 -> Hue[0.73, 1, 1], 3 -> Hue[0.14, 0.81, 0.99], 4 -> RGBColor[0, 0.56, 0], 5 -> RGBColor[0, 0.56, 1]}, ImageSize -> 30, Mesh -> True, MeshStyle -> Opacity[.15]] &)]
Out[10]=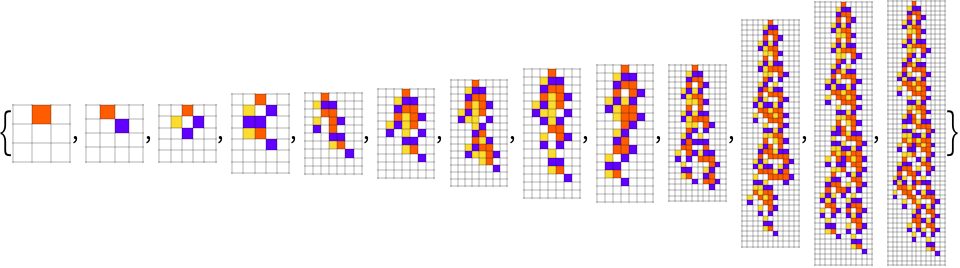

Search for longer automata:

In[11]:=
SeedRandom[1118]; ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {0, 4, 1}, "Depth" -> 500, "Cut" -> 200|>, "Breakthroughs", "Plot" -> 200]
Out[11]=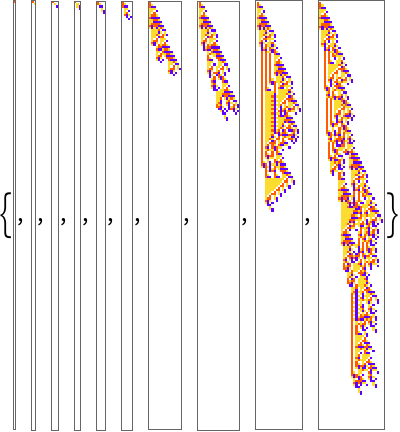

Evolve the initial conditions of a cellular automata:

In[12]:=
SeedRandom[444330]; ResourceFunction[ "AdaptiveCellularAutomaton"][<|"Rule" -> {1246491453600, 3, 1}, "InitialCondition" -> {CenterArray[1, 20], 0}, "MutationFunction" -> (<|"InitialCondition" -> {3, 1}|>), "Depth" -> 2000|>, "Breakthroughs", "Plot"]
Out[12]=

Evolve for width:

In[13]:=
SeedRandom[34460]; ResourceFunction[ "AdaptiveCellularAutomaton"][<| "Depth" -> 1000, "FitnessFunction" -> "Width"|>, "Breakthroughs", "Plot" -> 60]
Out[13]=

The default selection function accepts neutral mutations by default, make it so that it accepts mutations that decrease fitness by 1:

In[14]:=
SeedRandom[445550]; ResourceFunction[ "AdaptiveCellularAutomaton"][<| "Depth" -> 1000, "SelectionFunction" -> (#2 - #1 <= 1 &)|>, "Breakthroughs", "Plot" -> 50]
Out[14]=

Publisher

Willem Nielsen

Requirements

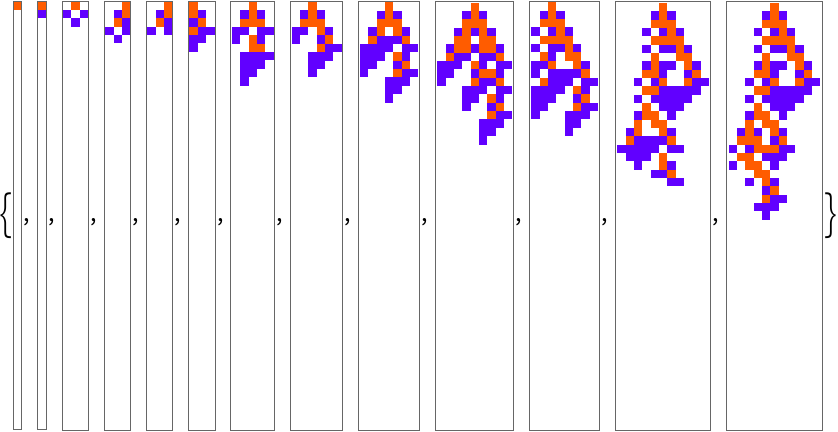Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 27 June 2025

Related Resources

License Information