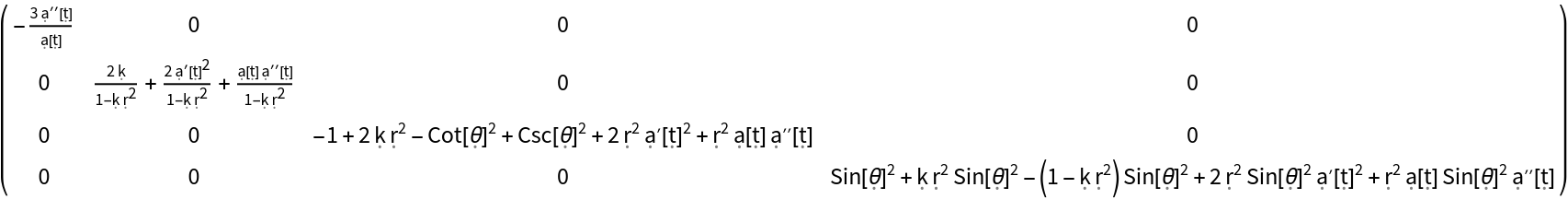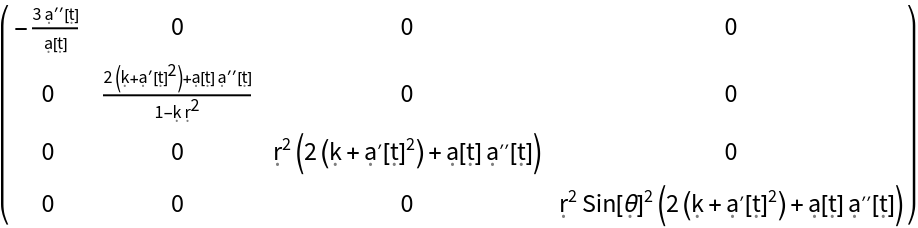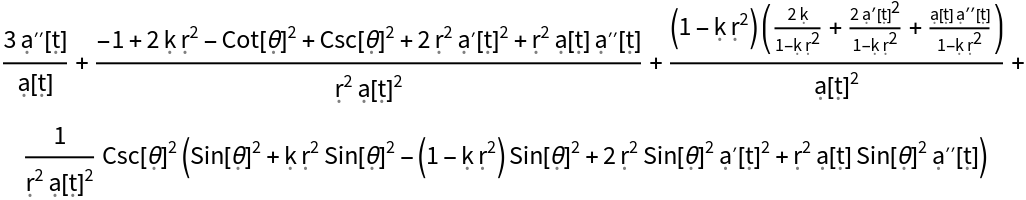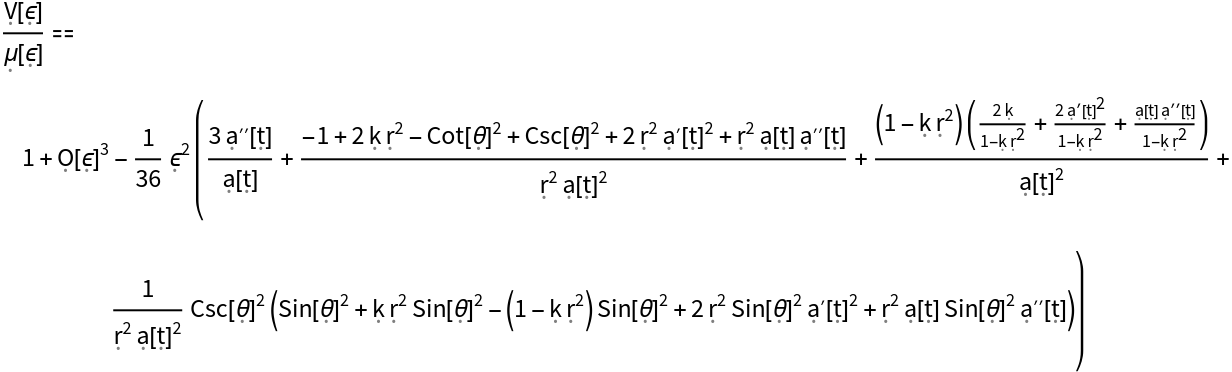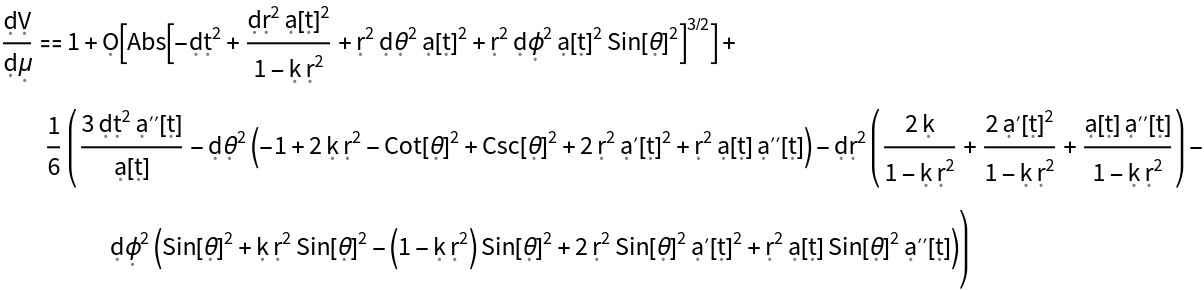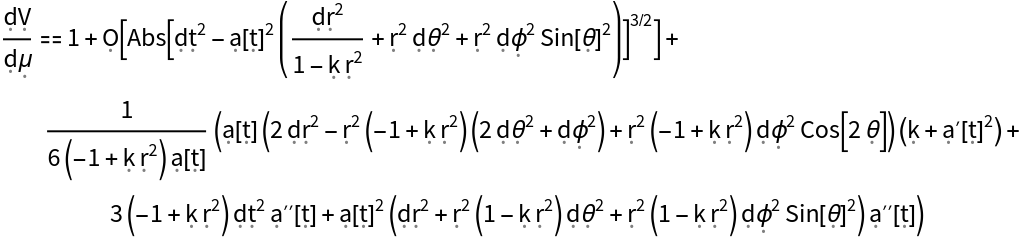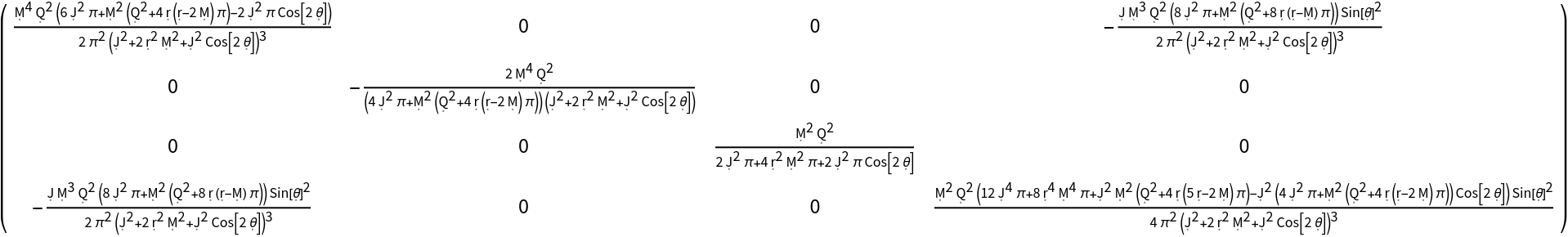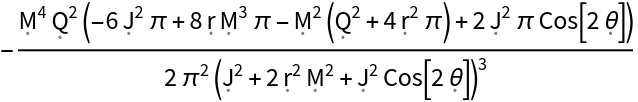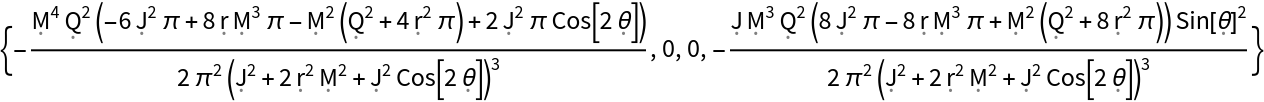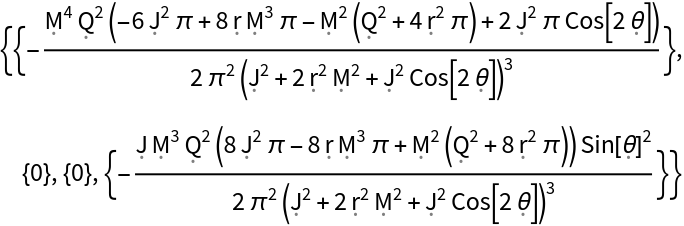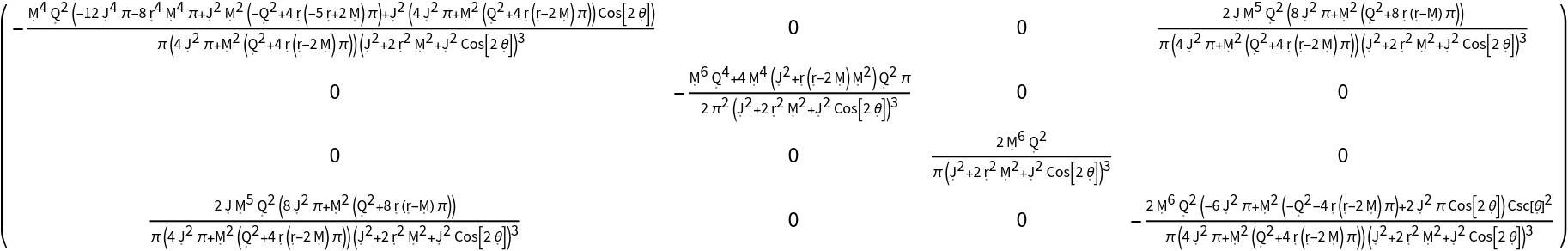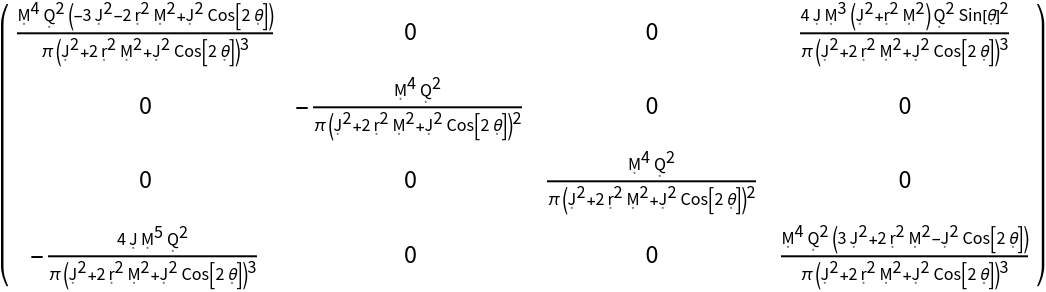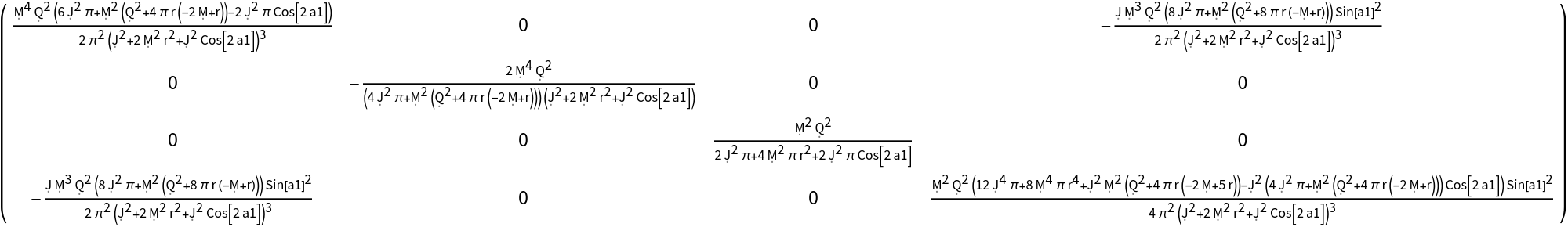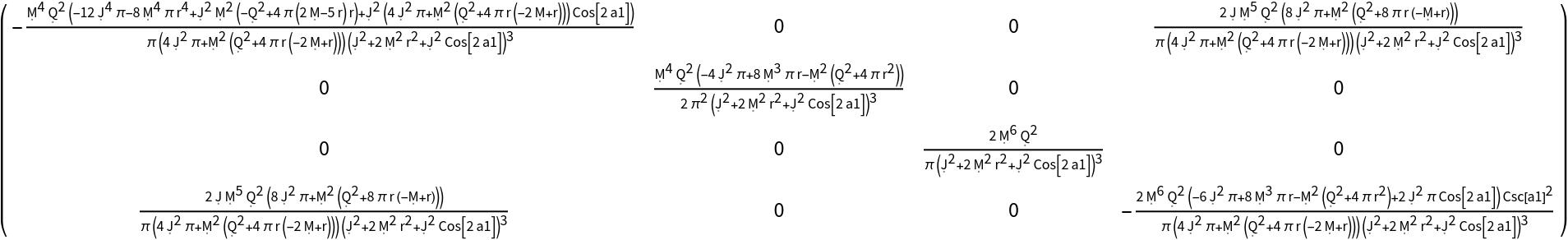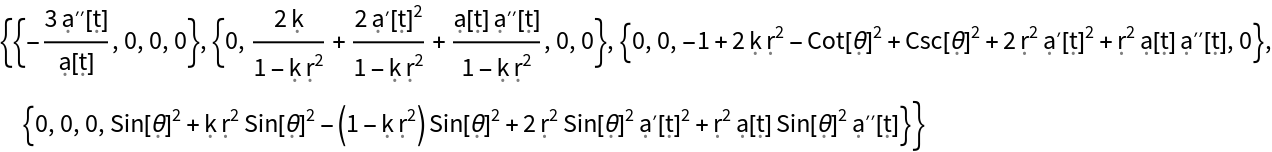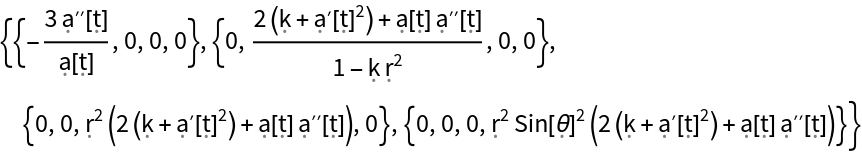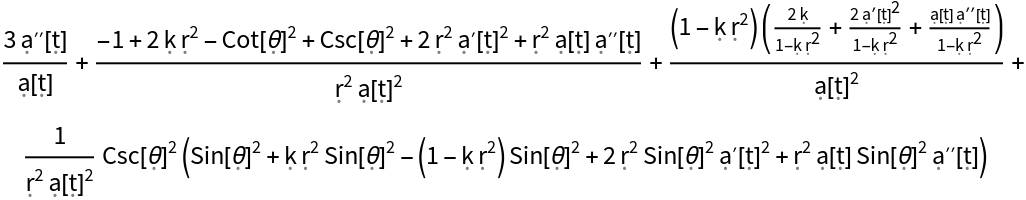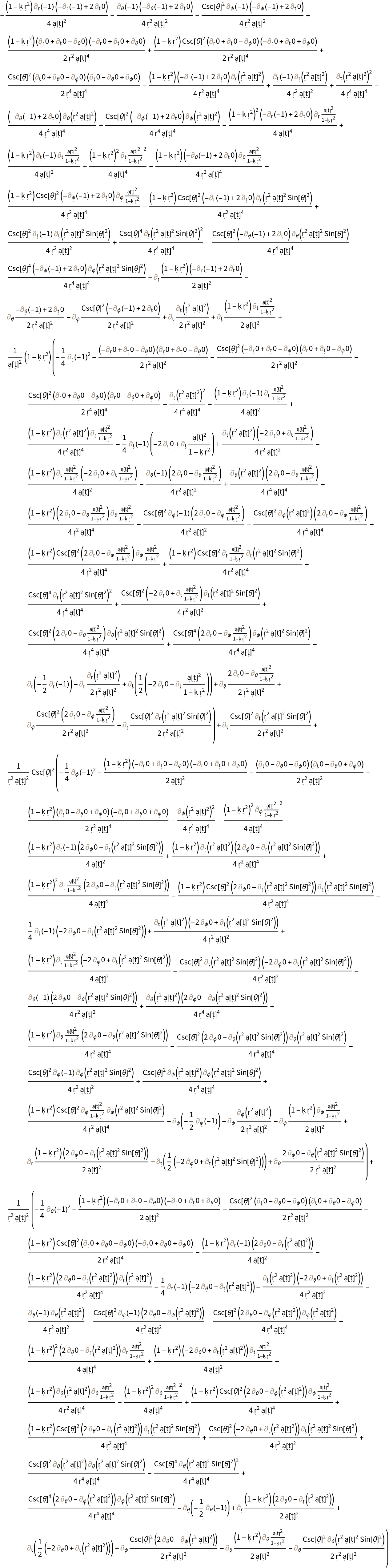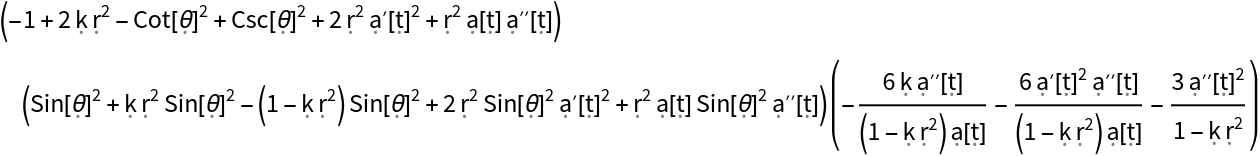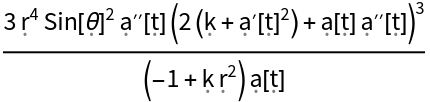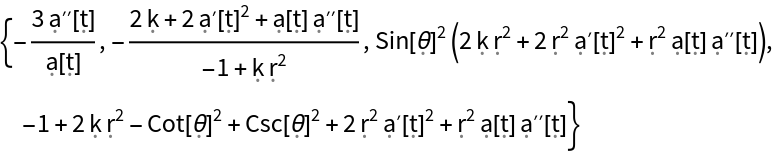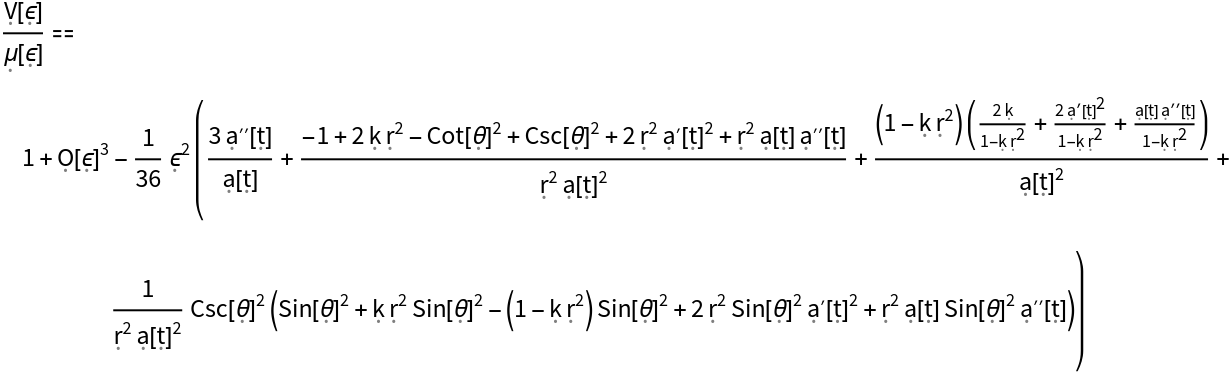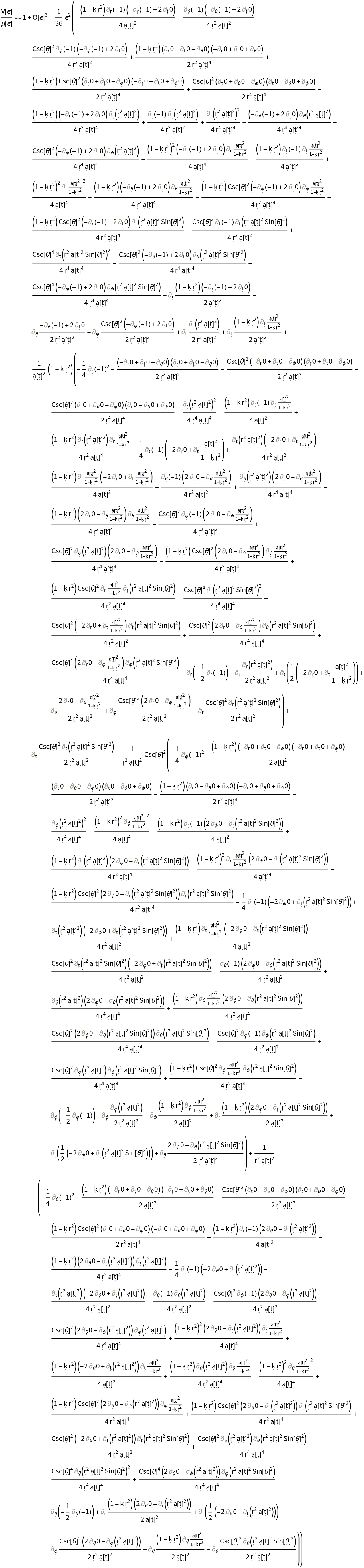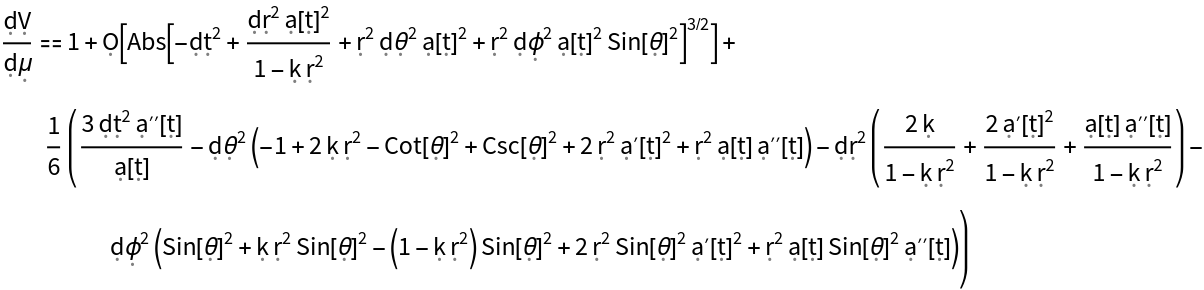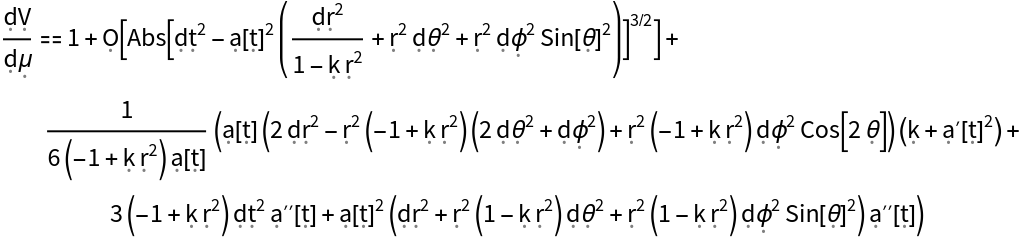Basic Examples (3)
Construct the Ricci curvature tensor for the Schwarzschild metric (e.g. for an uncharged, non-rotating black hole with symbolic mass M) in standard spherical polar coordinates:
Show the Ricci curvature tensor for the Schwarzschild metric in explicit (covariant) matrix form:
Show the Ricci curvature tensor for the Schwarzschild metric in explicit (covariant) matrix form, with all algebraic equivalences imposed:
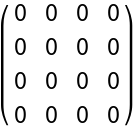
Deduce that the Schwarzschild metric is Ricci-flat:
Show the list of Schwarzschild coordinate symbols:
Show the list of differential 1-form symbols for each of the Schwarzschild coordinates:
Show the list of coordinate conditions that must hold for the Schwarzschild metric to be Lorentzian:
Construct the Ricci curvature tensor for the Friedmann-Lemaître-Robertson-Walker (FLRW) metric (for a homogeneous, isotropic and uniformly-expanding/contracting universe, with symbolic curvature parameter "k" and symbolic scale factor "a") in standard spherical polar coordinates:
Show the explicit matrix form, with all algebraic equivalences imposed:
Deduce that the FLRW metric is not Ricci-flat:
Show the list of conditions that must hold for the FLRW metric to be Ricci-flat:
Show the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor) for the FLRW metric:
Show the Ricci curvature scalar for the FLRW metric, with all algebraic equivalences imposed:
Deduce that the Ricci curvature scalar for the FLRW metric is non-vanishing:
Show the condition that must hold for the FLRW metric to have a vanishing Ricci curvature scalar:
Show the Taylor expansion for the volume of a small geodesic ball in the FLRW metric, as compared to the volume of a small geodesic ball of equivalent radius in flat/Minkowski spacetime:
Show the Taylor expansion for the volume of a small geodesic ball in the FLRW metric, with all algebraic equivalences imposed:
Show the Taylor expansion (along a Jacobi field) for the metric volume form in the FLRW metric, as compared to the metric volume form in flat/Minkowski spacetime:
Show the Taylor expansion (along a Jacobi field) for the metric volume form in the FLRW metric, with all algebraic equivalences imposed:
Show the list of coordinate values that cause the Ricci curvature tensor for the FLRW metric to become singular:
Show the list of coordinate values that cause the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor) for the FLRW metric to become singular, and note that they are the same as the above:
Show the association of all covariant derivatives (i.e. derivatives along tangent vectors of the manifold) of the Ricci curvature tensor for the FLRW metric:
Show the association of all covariant derivatives of the Ricci curvature tensor for the FLRW metric, with all algebraic equivalences imposed:
Show the list of all (contracted) Bianchi identities relating the covariant derivatives of the Ricci curvature tensor and the Ricci curvature scalar for the FLRW metric:
Show that the (contracted) Bianchi identities for the FLRW metric all hold identically:
Construct the Ricci curvature tensor for the Kerr-Newman metric (e.g. for a charged, spinning black hole with symbolic mass "M", symbolic angular momentum "J" and symbolic electric charge "Q") in Boyer-Lindquist/oblate spheroidal coordinates:
Extract (and simplify) the time-time component of the Ricci curvature tensor for the Kerr-Newman metric:
Extract (and simplify) the first row of the Ricci curvature tensor for the Kerr-Newman metric in matrix form:
Extract (and simplify) the first column of the Ricci curvature tensor for the Kerr-Newman metric in matrix form:
Compute the contravariant form of the Ricci curvature tensor (with both indices raised):
Compute a mixed form of the Ricci curvature tensor with one index raised/contravariant and one index lowered/covariant:
Transform to use the new coordinate symbols t, r, a1 and a2:
Transform to use the new coordinate symbols t, r, a1 and a2, and raise both indices, simultaneously:
Scope (3)
Ricci curvature tensors can be constructed directly from a MetricTensor expression:
Additional arguments can be used to specify the coordinate names (otherwise default symbols will be chosen automatically):
Or the indices (True for lowered/covariant and False for raised/contravariant - otherwise both indices will be set as lowered/covariant by default):
Or both simultaneously:
New coordinate symbols can be specified for any Ricci curvature tensor:
Indices can also be raised and lowered on any Ricci curvature tensor:
New coordinate symbols and new index positions can also be specified simultaneously:
Construct the Ricci curvature tensor for the FLRW metric, with symbolic curvature parameter "k" and symbolic scale factor "a":
Show the list of properties:
Show the explicit matrix representation of the Ricci curvature tensor:
Show the explicit matrix representation of the Ricci curvature tensor, with all algebraic equivalences imposed:
Show the explicit matrix representation of the Ricci curvature tensor, with all partial derivative operators left purely symbolic:
Show the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor):
Show the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor), with all algebraic equivalences imposed:
Show the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor), with all partial derivative operators left purely symbolic:
Show the metric tensor for the underlying manifold represented by the Ricci curvature tensor:
Show the list of coordinate symbols for the Ricci curvature tensor:
Show the list of differential 1-form symbols for the coordinates of the Ricci curvature tensor:
Show the list of booleans specifying the positions of the indices of the Ricci curvature tensor (True for lowered/covariant and False for raised/contravariant):
Determine whether the Ricci curvature tensor is covariant (i.e. both indices are lowered/covariant):
Determine whether the Ricci curvature tensor is contravariant (i.e. both indices are raised/contravariant):
Determine whether the Ricci curvature tensor is mixed (i.e. one index is lowered/covariant and one index is raised/contravariant):
Show a symbolic representation of the Ricci curvature tensor with appropriately raised/lowered indices:
Determine whether the underlying manifold is Ricci-flat (i.e. all components of the Ricci curvature tensor vanish):
Determine whether the underlying manifold has a vanishing Ricci curvature scalar (i.e. whether the trace of the Ricci curvature tensor vanishes):
Show the list of conditions required to guarantee that the underlying manifold is Ricci-flat (i.e. all components of the Ricci curvature tensor vanish):
Show the condition required to guarantee that the underlying manifold has a vanishing Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor vanished):
Show the association of all covariant derivatives (i.e. derivatives along tangent vectors of the underlying manifold) of the Ricci curvature tensor:
Show the association of all covariant derivatives (i.e. derivatives along tangent vectors of the underlying manifold) of the Ricci curvature tensor, with all algebraic equivalences imposed:
Show the association of all covariant derivatives (i.e. derivatives along tangent vectors of the underlying manifold) of the Ricci curvature tensor, with all partial derivative operators left purely symbolic:
Show the list of all (contracted) Bianchi identities relating the covariant derivatives of the Ricci curvature tensor and the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor):
Show the list of all (contracted) Bianchi identities relating the covariant derivatives of the Ricci curvature tensor and the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor), with all partial derivative operators left purely symbolic:
Show the number of dimensions of the underlying manifold represented by the Ricci curvature tensor:
Determine whether the Ricci curvature tensor is symmetric (in explicit, covariant matrix form):
Determine whether the Ricci curvature tensor is diagonal (in explicit, covariant matrix form):
Show the signature of the underlying manifold represented by the Ricci curvature tensor (with +1s representing positive eigenvalues and -1s representing negative eigenvalues of the metric tensor):
Determine whether the underlying manifold represented by the Ricci curvature tensor is Riemannian (i.e. all eigenvalues of the metric tensor have the same sign):
Determine whether the underlying manifold represented by the Ricci curvature tensor is pseudo-Riemannian (i.e. all eigenvalues are non-zero, but not all have the same sign):
Determine whether the underlying manifold represented by the Ricci curvature tensor is Lorentzian (i.e. all eigenvalues of the metric tensor have the same sign, except for one eigenvalue which has the opposite sign):
Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Ricci curvature tensor is Riemannian (i.e. all eigenvalues of the metric tensor are positive):
Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Ricci curvature tensor is pseudo-Riemannian (i.e. all eigenvalues are non-zero):
Show the list of conditions on the coordinates required to guarantee that the underlying manifold represented by the Ricci curvature tensor is Lorentzian (i.e. the "time" eigenvalue is negative, and all other eigenvalues are positive):
Show the list of coordinate values that cause the Ricci curvature tensor to become singular:
Show the list of coordinate values that cause the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor) to become singular:
Show the determinant of the Ricci curvature tensor (when represented as a covariant matrix):
Show the determinant of the Ricci curvature tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
Show the determinant of the Ricci curvature tensor (when represented as a covariant matrix), with all partial derivative operators left purely symbolic:
Show the eigenvalues of the Ricci curvature tensor (when represented as a covariant matrix):
Show the eigenvalues of the Ricci curvature tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
Show the eigenvectors of the Ricci curvature tensor (when represented as a covariant matrix):
Show the eigenvectors of the Ricci curvature tensor (when represented as a covariant matrix), with all algebraic equivalences imposed:
Compute the covariant form of the Ricci curvature tensor (with both indices lowered/covariant):
Compute the contravariant form of the Ricci curvature tensor (with both indices raised/contravariant):
Show the Taylor expansion for the volume "V" of a small geodesic ball of radius "ϵ", relative to the volume "" of the corresponding ball in flat/Euclidean space, represented in terms of the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor):
Show the Taylor expansion for the volume "V" of a small geodesic ball of radius "ϵ", relative to the volume "" of the corresponding ball in flat/Euclidean space, represented in terms of the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor), with all algebraic equivalences imposed:
Show the Taylor expansion for the volume "V" of a small geodesic ball of radius "ϵ", relative to the volume "" of the corresponding ball in flat/Euclidean space, represented in terms of the Ricci curvature scalar (i.e. the trace of the Ricci curvature tensor), with all partial derivative operators left purely symbolic:
Show the Taylor expansion (along a Jacobi field) for the metric volume form "dV", relative to the corresponding volume form "d" in flat/Euclidean space, represented in terms of projections of the Ricci curvature tensor:
Show the Taylor expansion (along a Jacobi field) for the metric volume form "dV", relative to the corresponding volume form "d" in flat/Euclidean space, represented in terms of projections of the Ricci curvature tensor, with all algebraic equivalences imposed:
Show the Taylor expansion (along a Jacobi field) for the metric volume form "dV", relative to the corresponding volume form "d" in flat/Euclidean space, represented in terms of projections of the Ricci curvature tensor, with all partial derivative operators left purely symbolic: