Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get permutations that satisfy a certain criterion
ResourceFunction["SelectPermutations"][list,crit] generates a list of all possible permutations of the elements in list satisfying crit. | |
ResourceFunction["SelectPermutations"][list,n,crit] gives all permutations containing at most n elements satisfying crit. | |
ResourceFunction["SelectPermutations"][list,{n},crit] gives all permutations containing exactly n elements satisfying crit. | |
ResourceFunction["SelectPermutations"][…,crit,m] gives at most m results. |
Select from the list {5,6,7,8,9} those permutations that form a prime when concatenating the digits:
| In[1]:= |
| Out[1]= |
Select those permutations having length 3:
| In[2]:= |
| Out[2]= |
Select those permutations having length 3–4:
| In[3]:= |
| Out[3]= |
Select permutations of {1,2,3,4} for which the first two elements and the last elements add up to the same value:
| In[4]:= |
| Out[4]= |
Select the first 10 permutations of length 4 for which the elements add up to an odd number:
| In[5]:= |
| Out[5]= |
Select polynomials for which the slope is 1 at x=0:
| In[6]:= |
| Out[6]= | 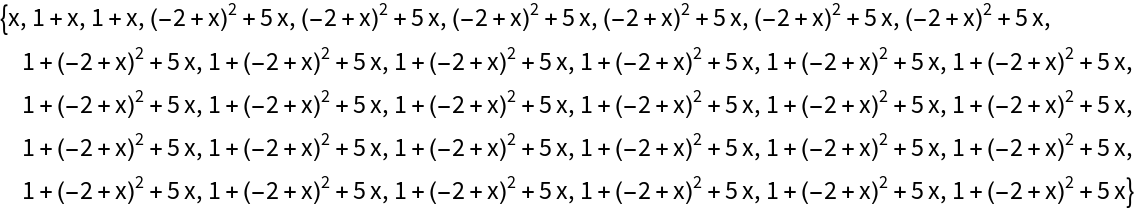 |
Confirm that the slope is indeed unity at x=0:
| In[7]:= |
| Out[7]= |
Duplicated items are treated the same:
| In[8]:= |
| Out[8]= |
The main difference between SelectPermutations[list,crit] and Select[Permutations[list],crit] is the memory usage:
| In[9]:= |
| Out[9]= |
Using Select and Permutations uses 500 times more memory:
| In[10]:= |
| Out[10]= |
Verify that the results are identical:
| In[11]:= |
| Out[11]= |
Head does not have to be List:
| In[12]:= |
| Out[12]= |
SelectPermutations might take longer as it is written in higher-level code as compared to the implementation of Permutations:
| In[13]:= | ![MaxMemoryUsed[
time = AbsoluteTiming[
result1 = ResourceFunction["SelectPermutations"][Range[3, 13], 6, Total[#] == 24 &];][[1]]];
Grid[{{"Time [sec]:", time}, {"Memory usage [bytes]:", %}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5df9855-467e-4f88-b851-d2e2d866e9af/213e6f23b0105f56.png) |
| Out[14]= |
Using the built-in functions is faster at the expense of 500× more memory:
| In[15]:= | ![MaxMemoryUsed[
time = AbsoluteTiming[
result2 = Select[Permutations[Range[3, 13], 6], Total[#] == 24 &];][[1]]];
Grid[{{"Time [sec]:", time}, {"Memory usage [bytes]:", %}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a5d/a5df9855-467e-4f88-b851-d2e2d866e9af/722f1ae559c84a7f.png) |
| Out[16]= |
This work is licensed under a Creative Commons Attribution 4.0 International License