Function Repository Resource:

MixedEulerianGraphQ

Test if a strongly connected mixed graph is Eulerian or unicursal

Contributed by: Peter Cullen Burbery

ResourceFunction["MixedEulerianGraphQ"][g]

yields True if the strongly connected mixed graph g is Eulerian or unicursal, and False otherwise.

Details

Eulerian graphs have applications in arc routing and operations research.

A mixed graph that is strongly connected is Eulerian, or unicursal, if and only if the graph is even (meaning all nodes/vertices are connected to an even number of other nodes/vertices and have an even degree) and the graph satisfied the balanced set condition, which states that for any subset of vertices/nodes, the difference between the number of arcs entering and the number of arcs leaving is less than or equal to the number of edges incident with the vertices/nodes.

Examples

Basic Examples (2)

Test if a mixed graph is Eulerian:

In[1]:=

$ResourceFunction["MixedEulerianGraphQ"][\!\(\* GraphicsBox[ NamespaceBox["NetworkGraphics", DynamicModuleBox[{Typeset`graph = HoldComplete[ Graph[{$CellContext`a, $CellContext`b, $CellContext`c, $CellContext`d, $CellContext`e, $CellContext`f}, {{{1, 2}, {4, 5}}, {{ 2, 3}, {3, 4}, {5, 6}, {1, 6}}}, {ImageSize -> Automatic, VertexLabels -> {Automatic}}]]}, TagBox[GraphicsGroupBox[{ {Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], {Arrowheads[0.], ArrowBox[{{1.4912694367624908`, 1.742714507353599}, { 0.4902731311139421, 1.7310116649185252`}}, 0.02261782466291873]}, ArrowBox[{{1.4912694367624908`, 1.742714507353599}, { 2.000783839713522, 0.8828679155736145}}, 0.02261782466291873], {Arrowheads[0.], ArrowBox[{{2.000783839713522, 0.8828679155736145}, { 1.5101005382159565`, 0.011615053838323175`}}, 0.02261782466291873]}, {Arrowheads[0.], ArrowBox[{{1.5101005382159565`, 0.011615053838323175`}, { 0.5099998752410617, 0.}}, 0.02261782466291873]}, ArrowBox[{{0.5099998752410617, 0.}, {0., 0.8594997331614967}}, 0.02261782466291873], {Arrowheads[0.], ArrowBox[{{0., 0.8594997331614967}, {0.4902731311139421, 1.7310116649185252`}}, 0.02261782466291873]}}, {Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[ 0.7]}], { DiskBox[{1.4912694367624908, 1.742714507353599}, 0.02261782466291873], InsetBox["a", Offset[{2, 2}, {1.5138872614254095, 1.7653323320165177}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}, { DiskBox[{2.000783839713522, 0.8828679155736145}, 0.02261782466291873], InsetBox["b", Offset[{2, 2}, {2.0234016643764408, 0.9054857402365333}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}, { DiskBox[{1.5101005382159565, 0.011615053838323175}, 0.02261782466291873], InsetBox["c", Offset[{2, 2}, {1.5327183628788752, 0.0342328785012419}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}, { DiskBox[{0.5099998752410617, 0.}, 0.02261782466291873], InsetBox["d", Offset[{2, 2}, {0.5326176999039804, 0.02261782466291873}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}, { DiskBox[{0., 0.8594997331614967}, 0.02261782466291873], InsetBox["e", Offset[{2, 2}, {0.02261782466291873, 0.8821175578244155}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}, { DiskBox[{0.4902731311139421, 1.7310116649185252}, 0.02261782466291873], InsetBox["f", Offset[{2, 2}, {0.5128909557768608, 1.753629489581444}], ImageScaled[{0, 0}], BaseStyle->"Graphics"]}}}], MouseAppearanceTag["NetworkGraphics"]], AllowKernelInitialization->False]], DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]}, FormatType->TraditionalForm, FrameTicks->None, ImageSize->Automatic]\)]$

Out[1]=

Although this graph is even, the graph violates the balanced set condition and is therefore not Eulerian:

In[2]:=

$gr = Graph[{a -> b, b \[UndirectedEdge] c, c \[UndirectedEdge] d, d -> b, d \[UndirectedEdge] e, d -> f, f \[UndirectedEdge] a, e -> b}, VertexLabels -> Automatic, GraphLayout -> "PlanarEmbedding"]$

Out[2]=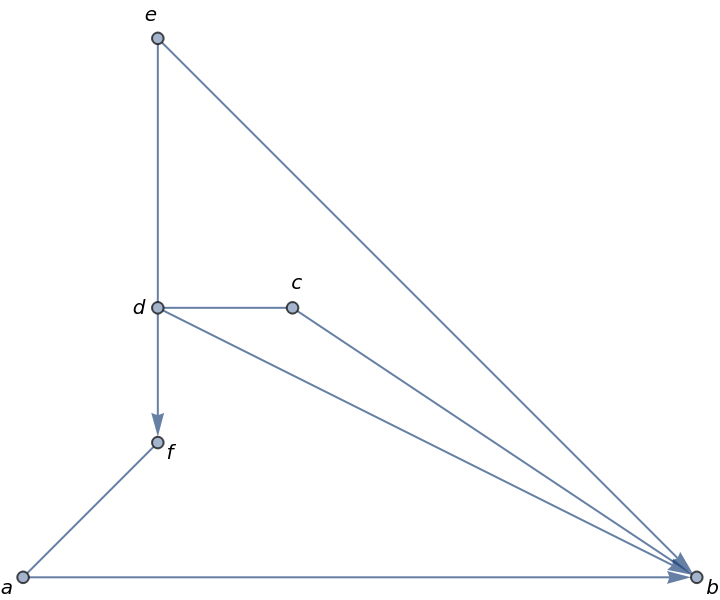

In[3]:=

Out[3]=

Possible Issues (1)

A graph that is beyond a limit of around 14 nodes can take an unreasonable amount of time because the number n of subsets grows exponentially according to O(2ⁿ):

In[4]:=

$ResourceFunction["MixedEulerianGraphQ"][ Graph[{a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v}, {a -> b, b \[UndirectedEdge] c, c \[UndirectedEdge] d, d -> b, d \[UndirectedEdge] e, d -> f, f \[UndirectedEdge] a, e -> b, g \[UndirectedEdge] e, h \[UndirectedEdge] g, i \[UndirectedEdge] g, j \[UndirectedEdge] e, k \[UndirectedEdge] j, l \[UndirectedEdge] k, m \[UndirectedEdge] l, n \[UndirectedEdge] m, m \[UndirectedEdge] o, o \[UndirectedEdge] p, p \[UndirectedEdge] q, q \[UndirectedEdge] r, r \[UndirectedEdge] s, s \[UndirectedEdge] t, t \[UndirectedEdge] u, u \[UndirectedEdge] v}]] // AbsoluteTiming$

Out[4]=

Publisher

Peter Burbery

Version History

1.0.0 – 23 August 2022

Related Resources

Author Notes

I wrote this function because EulerianGraphQ does not work on mixed graphs.

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License