Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get a numerically sorted list of abscissa-weight pairs for Gaussian quadrature
ResourceFunction["GaussianQuadratureWeights"][n,{a,b}] gives a list of the n pairs {xi,wi} of the elementary n-point Gaussian formula for quadrature on the interval a to b, where wi is the weight of the abscissa xi. | |
ResourceFunction["GaussianQuadratureWeights"][n,{a,b},prec] uses the working precision prec. |
The abscissas and weights for a 10-point quadrature on a given interval:
| In[1]:= |
| Out[1]= |
The exact abscissas and weights:
| In[2]:= |
| Out[2]= |
Use the specified precision:
| In[3]:= |
| Out[3]= |
Use the Gaussian quadrature to approximate the area under a curve:
| In[4]:= |
| Out[4]= |
Plot the curve over a given interval:
| In[5]:= |
| Out[5]= | 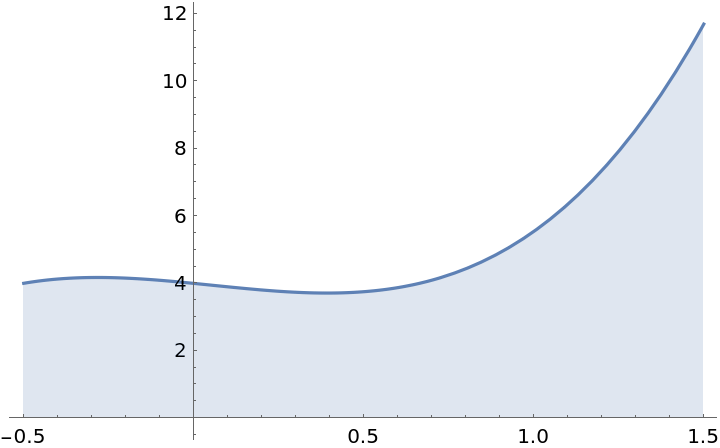 |
Approximate the area under the curve for a specific n:
| In[6]:= | ![area[n_] := Module[{a, w}, {a, w} = Transpose@
ResourceFunction["GaussianQuadratureWeights"][n, {-0.5, 1.5}]; w . (f /@ a)]](https://www.wolframcloud.com/obj/resourcesystem/images/a58/a586a1c2-052f-4f50-9957-aa8f02193681/3d0f4f0315cb3618.png) |
| In[7]:= |
| Out[7]= |
Compare to the output of NIntegrate:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
The difference in Gaussian quadratures of two different orders:
| In[10]:= |
| Out[10]= |
The abscissas and weights for an n-point quadrature on {-1,1} for n=2 … 5:
| In[11]:= |
| Out[11]= | 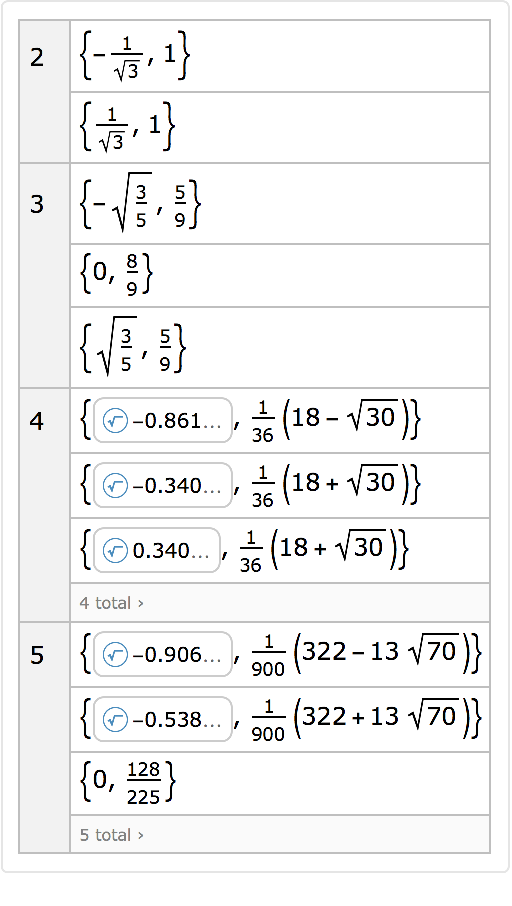 |
The triangle of polynomials whose roots determine the weights for n up to 8:
| In[12]:= | ![Dataset@Table[
Association[
n -> TraditionalForm@
MinimalPolynomial[
ResourceFunction["GaussianQuadratureWeights"][n, {-1, 1}][[1, 2]], x]], {n, 8}]](https://www.wolframcloud.com/obj/resourcesystem/images/a58/a586a1c2-052f-4f50-9957-aa8f02193681/6224934e6b4c639a.png) |
| Out[12]= |  |
For the interval {-1,1}, abscissas for the n-point Gaussian quadrature are the roots of the Legendre polynomial Pn(x):
| In[13]:= |
| In[14]:= |
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
The weights at abscissas xi are 2(1-xi2)/((n+1)2Pn+1(xi))2):
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
The sum of the weights is exactly 2:
| In[19]:= |
| Out[19]= |
Resource function GaussianQuadratureError gives an upper bound of the error in the weights used for the approximation:
| In[20]:= |
| Out[20]= |
The abscissas and weights for the elementary n-point Gaussian quadrature are related to the eigensystem of the n⨯n symmetric tridiagonal Gaussian quadrature matrix:
| In[21]:= |
| In[22]:= |
| In[23]:= |
| Out[23]= | 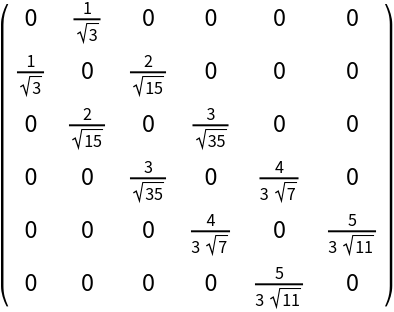 |
Eigenvalues of the matrix determine the abscissas:
| In[24]:= |
| Out[24]= |  |
| In[25]:= |
| Out[25]= |
Eigenvectors of the matrix determine the weights:
| In[26]:= |
| In[27]:= |
| Out[27]= |
This work is licensed under a Creative Commons Attribution 4.0 International License