Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 MatrixNorm

Source Notebook

Estimate the Hölder p-norm of a numerical matrix

Contributed by: Jan Mangaldan

ResourceFunction["MatrixNorm"][m,p]

gives an estimate of the Hölder p-norm of the numerical matrix m.

Details and Options

If the elements of m are exact numbers, ResourceFunction["MatrixNorm"] applies N to them.
For p⩵1 or p⩵∞, ResourceFunction["MatrixNorm"][m,p] is equivalent to Norm[m,p].
ResourceFunction["MatrixNorm"] takes the following options:
"Samples"9number of samples taken for estimation
ToleranceAutomatictolerance for accepting a norm estimate

Examples

Basic Examples (2) 

Estimate the 2-norm of a rectangular matrix:

In[1]:=
ResourceFunction["MatrixNorm"][( { {1, 2}, {3, 4}, {5, 6} } ), 2]
Out[1]=

Compare with the result of Norm:

In[2]:=
Norm[N[( { {1, 2}, {3, 4}, {5, 6} } )], 2]
Out[2]=

Scope (2) 

Estimate the 4-norm of a matrix:

In[3]:=
ResourceFunction["MatrixNorm"][( { {1, 2}, {3, 4}, {5, 6} } ), 4]
Out[3]=

Estimate the 4-norm to arbitrary precision:

In[4]:=
ResourceFunction["MatrixNorm"][N[( { {1, 2}, {3, 4}, {5, 6} } ), 25], 4]
Out[4]=

Plot the p-norm of a matrix with varying p:

In[5]:=
Plot[ResourceFunction["MatrixNorm"][( { {1, 2}, {3, 4}, {5, 6} } ), p], {p, 1, 9}, {Frame -> True, FrameLabel -> { Style["p", Italic], "\!\(\*SubscriptBox[RowBox[{\"\[LeftDoubleBracketingBar]\", \"A\", \"\[RightDoubleBracketingBar]\"}], \"p\"]\)"}}]
Out[5]=

Options (2) 

Samples (1) 

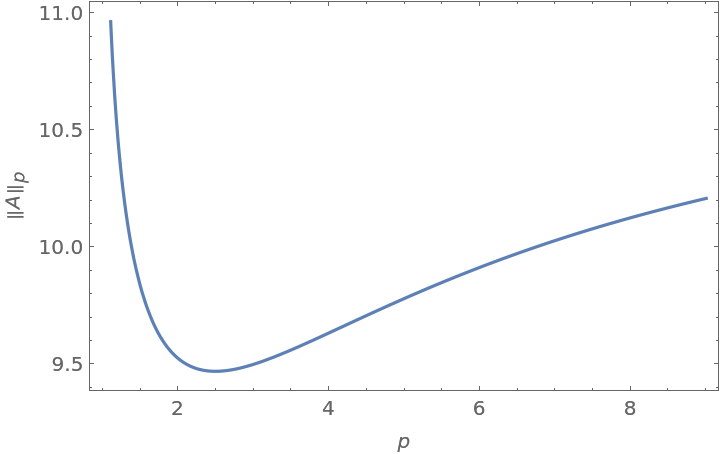Increase the "Samples" setting to get a better estimate:

In[6]:=
ResourceFunction["MatrixNorm"][N[({ {2, 1, 4}, {3, 0, -1}, {1, 1, 2} }), 20], 3]
Out[6]=
In[7]:=
ResourceFunction["MatrixNorm"][N[({ {2, 1, 4}, {3, 0, -1}, {1, 1, 2} }), 20], 3, "Samples" -> 21]
Out[7]=

Tolerance (1) 

Lower the Tolerance setting to get a better estimate:

In[8]:=
ResourceFunction["MatrixNorm"][N[({ {2, 1, 4}, {3, 0, -1}, {1, 1, 2} }), 20], 3]
Out[8]=
In[9]:=
ResourceFunction["MatrixNorm"][N[({ {2, 1, 4}, {3, 0, -1}, {1, 1, 2} }), 20], 3, Tolerance -> 10^-12]
Out[9]=

Properties and Relations (3) 

MatrixNorm[m,1] is equivalent to Norm[m,1]:

In[10]:=
{ResourceFunction["MatrixNorm"][N[( { {1, 2}, {3, 4}, {5, 6} } )], 1], Norm[N[( { {1, 2}, {3, 4}, {5, 6} } )], 1]}
Out[10]=

MatrixNorm[m,∞] is equivalent to Norm[m,∞]:

In[11]:=
{ResourceFunction["MatrixNorm"][N[( { {1, 2}, {3, 4}, {5, 6} } )], \[Infinity]], Norm[N[( { {1, 2}, {3, 4}, {5, 6} } )], \[Infinity]]}
Out[11]=

For 1<p<∞, MatrixNorm usually gives a good estimate of the p-norm, with less time and effort:

In[12]:=
AbsoluteTiming[NMaxValue[Norm[( { {1, 2}, {3, 4}, {5, 6} } ) . x, 4]/Norm[x, 4], x \[Element] FullRegion[2]]]
Out[12]=
In[13]:=
AbsoluteTiming[ResourceFunction["MatrixNorm"][( { {1, 2}, {3, 4}, {5, 6} } ), 4]]
Out[13]=

Possible Issues (2) 

MatrixNorm only works for numerical matrices:

In[14]:=
ResourceFunction["MatrixNorm"][( { {x, y}, {z, w} } ), 2]
Out[14]=
In[15]:=
ResourceFunction["MatrixNorm"][{1, -1, 2}, 2]
Out[15]=

MatrixNorm only estimates p-norms for p>1:

In[16]:=
ResourceFunction["MatrixNorm"][( { {1, 2}, {3, 4} } ), 1/2]
Out[16]=

Version History

  • 1.0.1 – 04 January 2021
  • 1.0.0 – 21 December 2020

Source Metadata

  • Citation:
    • Higham N.J., "Estimating the matrix p-norm." Numerische Mathematik, vol. 62, 539–555, 1992. DOI: 10.1007/BF01396242
    • Boyd D.W., "The power method for l^p norms." Linear Algebra and its Applications, vol. 9, 95-101, 1974. DOI:10.1016/0024-3795(74)90029-9

Related Resources

License Information