Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute polygons for hyperbolic tilings
ResourceFunction["HyperbolicTiling"][p,q,n] gives a list of polygons representing the hyperbolic tiling of p,q, and n. |
| "Primal" | polygons are positioned around a center coordinate (default) |
| "Dual" | the corresponding dual polygons for the hyperbolic tiling |
Generate two layers of hyperbolic tiles, where each polygon has four sides and five polygons meet at each vertex:
| In[1]:= |
| Out[1]= |
Visualize the result:
| In[2]:= |
| Out[2]= | 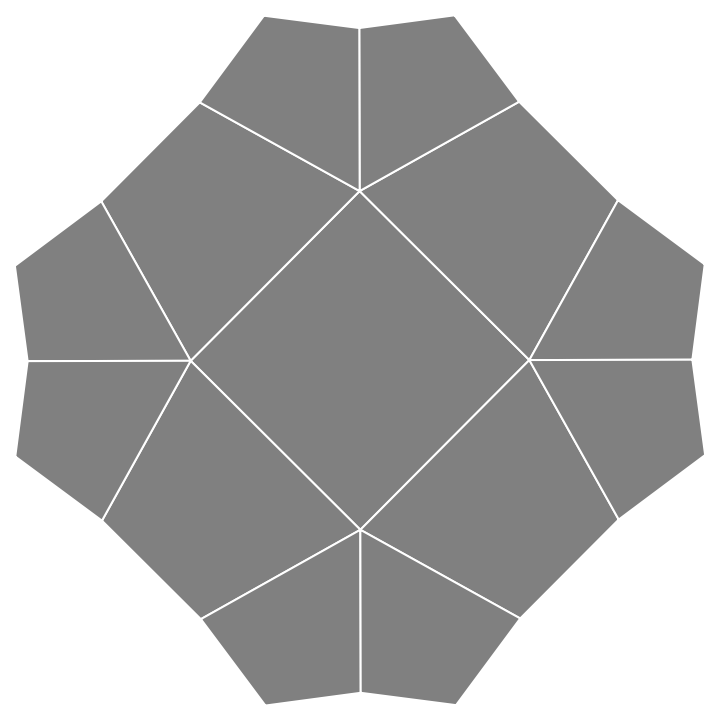 |
Generate three layers of seven-sided polygons where three polygons meet at each vertex:
| In[3]:= |
| Out[3]= |  |
A slightly more complex tiling:
| In[4]:= |
| Out[4]= |  |
Compare the "Primal" and "Dual" methods:
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
| In[7]:= | ![GraphicsGrid[{{
Graphics[{EdgeForm[White], FaceForm[Gray], tilesPrimal}],
Graphics[{EdgeForm[White], FaceForm[Gray], tilesDual}]
}}]](https://www.wolframcloud.com/obj/resourcesystem/images/a39/a3982f86-9de2-435a-8347-7bba0f0beec7/50827da03067aa96.png) |
| Out[7]= | 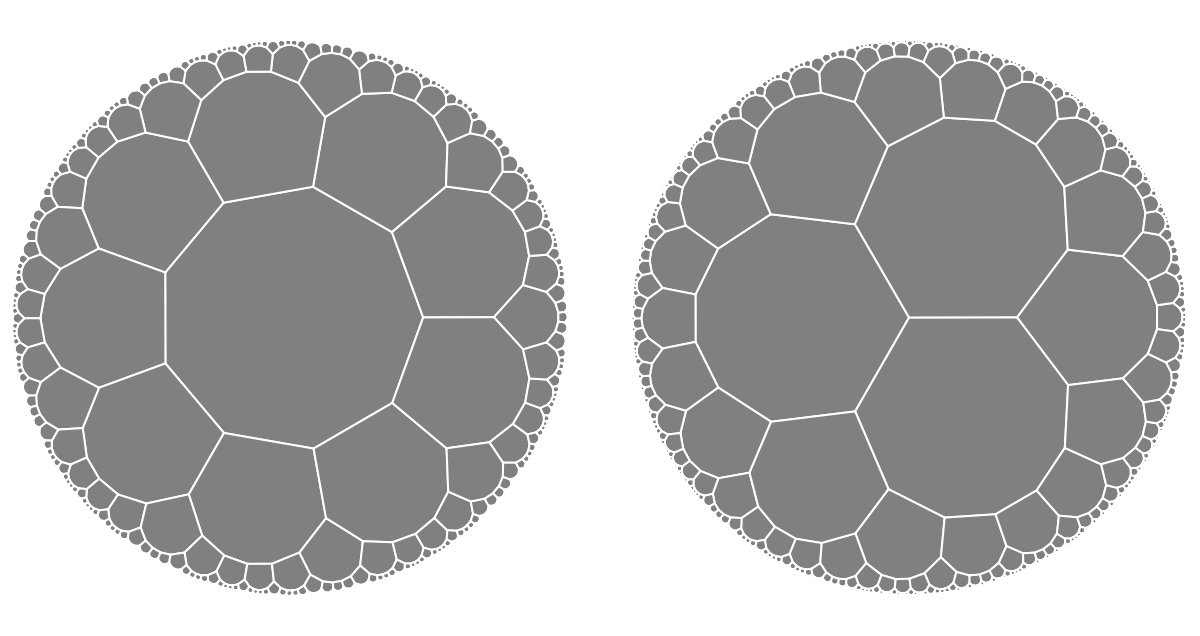 |
| In[8]:= |
| Out[8]= |
Get the tiles:
| In[9]:= |
| Out[9]= |
Get the individual polygons:
| In[10]:= |
Animate the incremental drawing of the polygons:
| In[11]:= | ![Manipulate[
Graphics[
{EdgeForm[White], FaceForm[Gray], Take[polys, n]}, PlotRange -> 1.2],
{n, 1, Length[polys], 1}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/a39/a3982f86-9de2-435a-8347-7bba0f0beec7/482f9d5c868a0123.png) |
| Out[11]= | 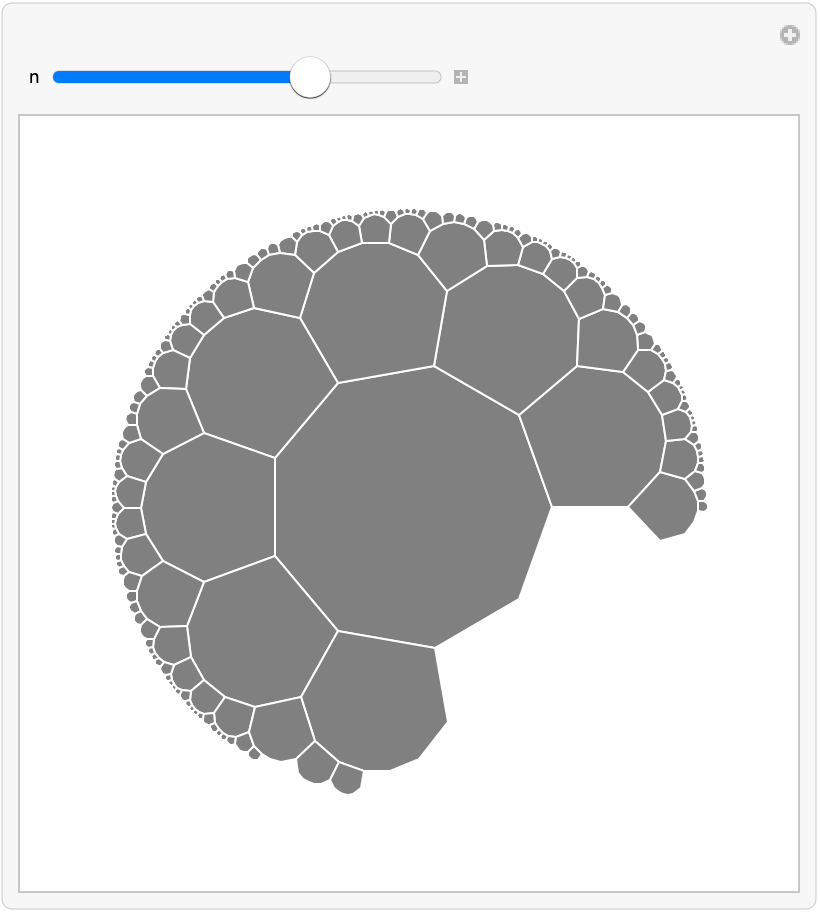 |
Use the HyperbolicPoincarePolygon resource function to convert the polygons to Poincaré polygons:
| In[12]:= |
| In[13]:= |
| In[14]:= |
| Out[14]= | 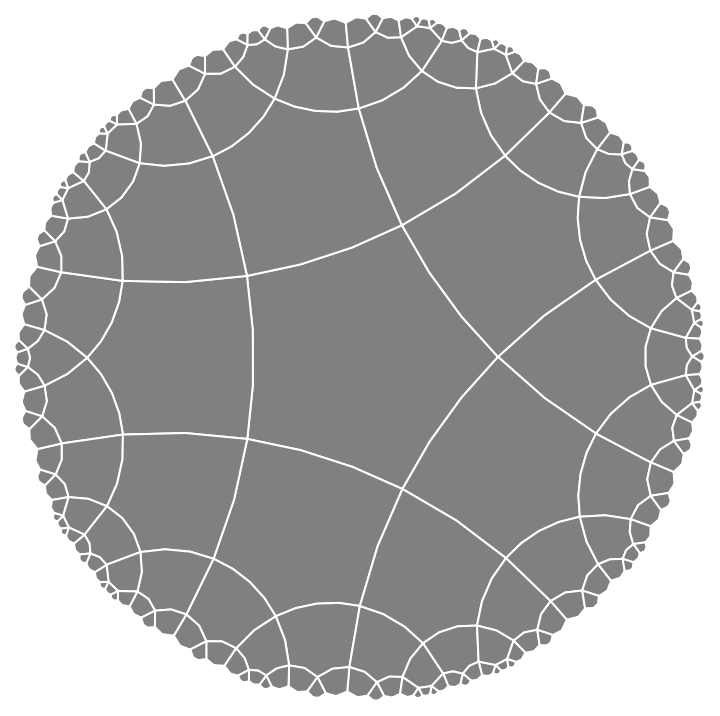 |
Wolfram Language 14.0 (January 2024) or above
This work is licensed under a Creative Commons Attribution 4.0 International License