Function Repository Resource:

ZolotarevZ

Evaluate the Zolotarev polynomial

Contributed by: Jan Mangaldan

ResourceFunction["ZolotarevZ"][p,q,x,m]

gives the Zolotarev polynomial Z_p,q(x|m).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.

The Zolotarev polynomial Z_p,q(x|m) with elliptic parameter m is the polynomial that least deviates from zero, such that it has p zeroes to the left of its global maximum in [-1,1] and q zeroes to the right of it.

Z_p,q(x|m) is a polynomial of degree p+q.

For certain special arguments, ResourceFunction["ZolotarevZ"] automatically evaluates to exact values.

ResourceFunction["ZolotarevZ"] can be evaluated to arbitrary numerical precision.

ResourceFunction["ZolotarevZ"] automatically threads over lists.

Examples

Basic Examples (2)

Evaluate numerically:

In[1]:=

Out[1]=

Plot over a subset of the reals:

In[2]:=

Out[2]=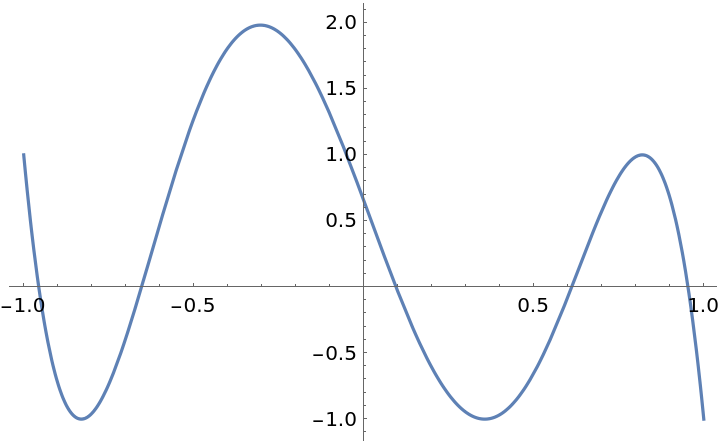

Scope (3)

Evaluate to high precision:

In[3]:=

Out[3]=

Evaluate with symbolic argument and numerical parameter:

In[4]:=

Out[4]=

ZolotarevZ threads elementwise over lists:

In[5]:=

Out[5]=

Applications (2)

Plot a Zolotarev polynomial and show the location of its global maximum in [-1,1]:

In[6]:=

$With[{p = 9, q = 5, m = (78/100)^2}, Plot[ResourceFunction["ZolotarevZ"][p, q, x, m], {x, -1, 1}, Axes -> None, Frame -> True, GridLines -> {{2 JacobiCN[q/(p + q) EllipticK[m], m]^2 - 1 + 2 JacobiCN[q/(p + q) EllipticK[m], m] JacobiSD[ q/(p + q) EllipticK[m], m] JacobiZN[q/(p + q) EllipticK[m], m]}, None}, PlotRange -> All]]$

Out[6]=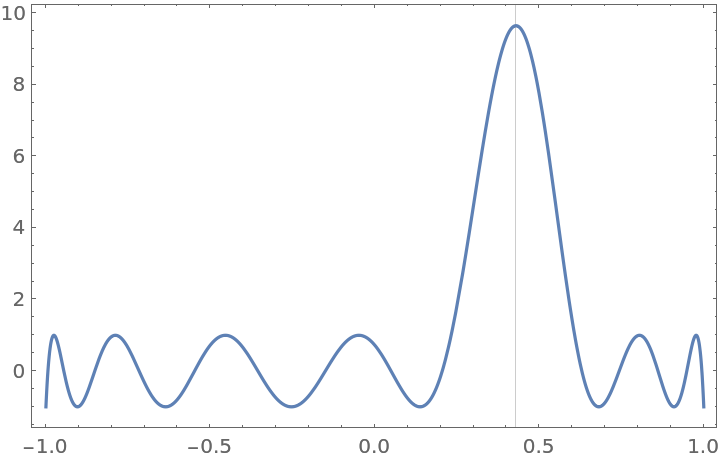

Compare a Zolotarev polynomial with a Chebyshev polynomial of the same degree:

In[7]:=

$Manipulate[ Plot[{ResourceFunction["ZolotarevZ"][p, q, x, m], (-1)^q ChebyshevT[p + q, x]}, {x, -1, 1}, Axes -> None, Frame -> True, PlotRange -> All], {{p, 9}, 1, 10, 1}, {{q, 5}, 1, 10, 1}, {{m, 1/2}, 0, 1}]$

Out[7]=

Properties and Relations (2)

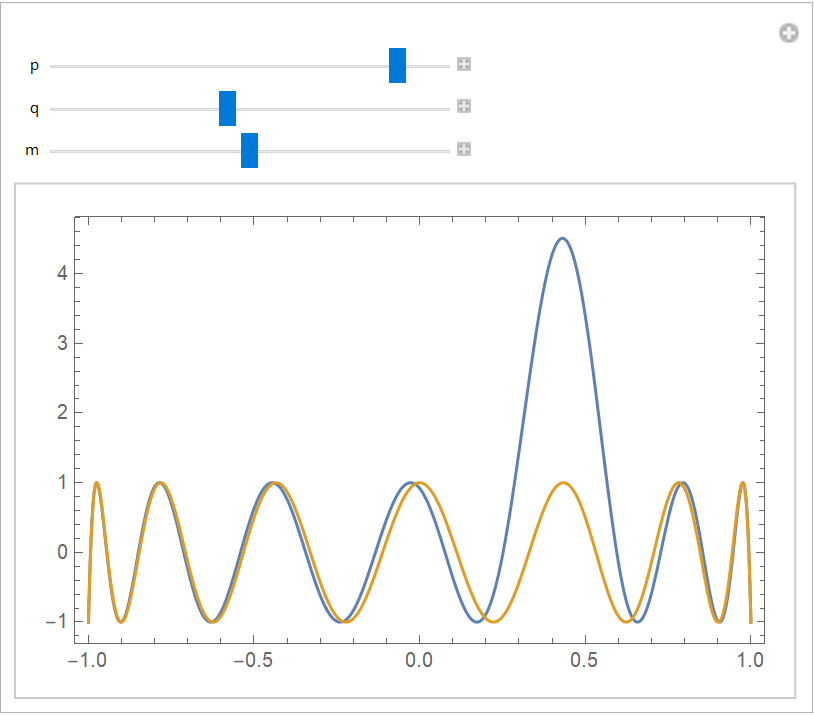When m=0 or m=1, the Zolotarev polynomial is a scalar multiple of the Chebyshev polynomial ChebyshevT:

In[8]:=

$With[{p = 2, q = 3}, ResourceFunction["ZolotarevZ"][p, q, z, 0] == (-1)^ q ChebyshevT[p + q, z]] // Simplify$

Out[8]=

In[9]:=

$With[{p = 2, q = 3}, ResourceFunction["ZolotarevZ"][p, q, z, 1] == (-1)^q/2^( 2 (p + q) - 1) ChebyshevT[p + q, z]] // Simplify$

Out[9]=

A parametric representation of the Zolotarev polynomial:

In[10]:=

$xzolo[p_, q_, u_, m_] := With[{rk = q/(p + q) EllipticK[m]}, JacobiCN[rk, m]^2 (JacobiSN[u, m]^2 + JacobiSN[rk, m]^2)/( JacobiSN[u, m]^2 - JacobiSN[rk, m]^2) - JacobiSN[rk, m]^2]$

In[11]:=

$yzolo[p_, q_, u_, m_] := With[{rk = q/(p + q) EllipticK[m]}, (-1)^ q ChebyshevT[p + q, 1/2 (NevilleThetaS[u - rk, m]/NevilleThetaS[u + rk, m] + NevilleThetaS[u + rk, m]/NevilleThetaS[u - rk, m])]]$

Check equivalence with the explicit representation:

In[12]:=

Out[12]=

Possible Issues (1)

The literature sometimes uses a different definition of the Zolotarev polynomial, where the polynomial is defined to have p zeroes in [-1,1]:

In[13]:=

$newZolo[p_, q_, x_, m_] := With[{rk = q/(p + q) EllipticK[m]}, ResourceFunction["ZolotarevZ"][p, q, JacobiCN[rk, m]^2 x - JacobiSN[rk, m]^2, m]]$

In[14]:=

Out[14]=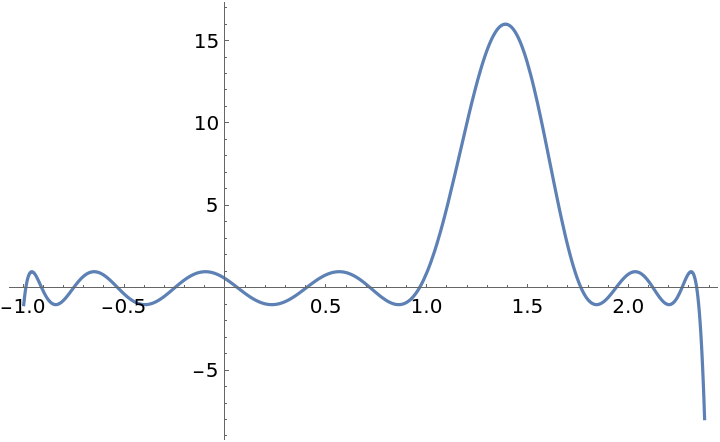

Version History

1.0.0 – 20 January 2021

Source Metadata

Citation:
- Chen X., Parks T.W., "Analytic design of optimal FIR narrow-band filters using Zolotarev polynomials." IEEE Transactions on Circuits and Systems, vol. CAS-33, no. 11, 1065-1071, 1986. DOI: 10.1109/tcs.1986.1085868
- Vlcek M., Unbehauen R., "Zolotarev polynomials and optimal FIR filters." IEEE Transactions on Signal Processing, vol. 47, no. 3, 717-730, 1999. DOI: 10.1109/78.747778
- Carlson B.C., Todd J., "Zolotarev's first problem - the best approximation by polynomials of degree ≤ n-2 to x^n - n σ x^{n-1} in [-1,1]." Aequationes Mathematicae, vol. 26, 1-33, 1983. DOI: 10.1007/BF02189661

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

ZolotarevZ

Details