Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ZXDiagramToQuantumDiscreteOperator

Source Notebook

Convert a ZX-diagram into a discrete quantum operator

Contributed by: Jonathan Gorard (with modifications by Manojna Namuduri)

ResourceFunction["ZXDiagramToQuantumDiscreteOperator"][ZXDiagramObject[…]]

converts the specified ZXDiagramObject into an equivalent QuantumDiscreteOperator.

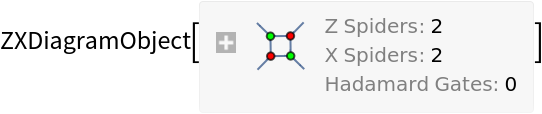
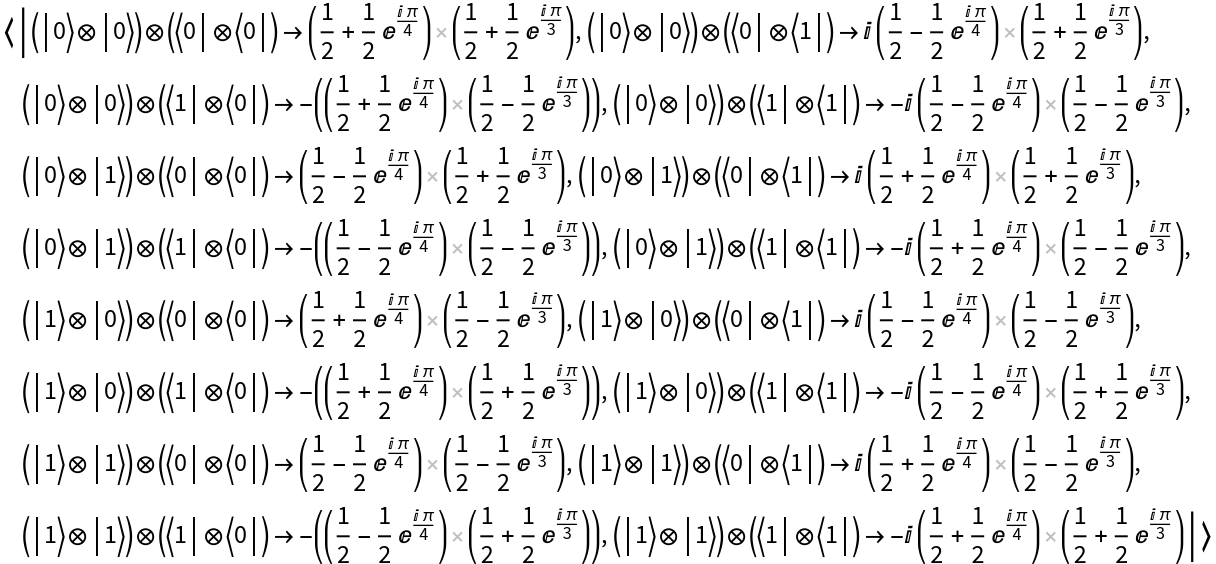Details

If ResourceFunction["ZXDiagramToQuantumDiscreteOperator"] succeeds in converting the specified ZXDiagramObject into a discrete quantum operator, it will return a QuantumDiscreteOperator object.
ResourceFunction["ZXDiagramToQuantumDiscreteOperator"] works by converting each sequential composition of Z-spider and X-spider generators into sequential compositions of rotations around the z axis and the x axis of the Bloch sphere, respectively, before eventually taking the tensor product of all such compositions to yield the desired QuantumDiscreteOperator.
The generators/spiders within the specified ZXDiagramObject may have arbitrary input and output arities.
In the resulting QuantumDiscreteOperator, the following properties are supported:
"Operator"association <|b11→e11,b12→e12,…|> of tensor products of basis names and matrix elements
"Basis"which QuantumBasis the operator is defined with respect to
"Picture"which quantum mechanical picture the operator is defined with respect to
"BasisElements"list of basis elements bi
"MatrixRepresentation"matrix representation mat of the operator
"OrderedMatrixRepresentation"matrix representation adjusted according to the order of the operator, assuming an input state containing Max[order] qudits (subsystems)
{"OrderedMatrixRepresentation",n}matrix representation adjusted according to the order of the operator, assuming an input state containing n qudits (subsystems)
"Arity"arity of the operator
"Dimensions"dimensionality of each qudit (subsystem) in the input state for the operator
"Order"order in which the operator should be applied to qudits (subsystems) in the input state
"HermitianQ"whether the operator is Hermitian (self-adjoint)
"UnitaryQ"whether the operator is unitary (an automorphism of Hilbert space)
"Eigenvalues"eigenvalues of the matrix representation of the operator
"Eigenvectors"eigenvectors of the matrix representation of the operator
"Properties"list of all property names
The default convention is to name Z-spiders as z1,z2,…; X-spiders as x1,x2,…; black diamonds as d1,d2,…; inputs as i1,i2,…; outputs as o1,o2,…; etc.

Examples

Basic Examples (4) 

Convert a single-spider ZX-diagram (representing a Pauli-Z gate) into an arity-1 discrete quantum operator:

In[1]:=
diagram = ResourceFunction[ "MakeZXDiagram"][{\[FormalCapitalZ][z, 0, 1, Pi], \[FormalCapitalW][z, o]}]
Out[1]=
In[2]:=
diagram["LabeledGraph"]
Out[2]=
In[3]:=
operator = ResourceFunction["ZXDiagramToQuantumDiscreteOperator"][diagram]
Out[3]=
In[4]:=
operator["Operator"]
Out[4]=

Convert a three-spider ZX-diagram (representing a Hadamard gate) into an arity-1 discrete quantum operator:

In[5]:=
diagram2 = ResourceFunction[ "MakeZXDiagram"][{\[FormalCapitalZ][z1, 1, 1, Pi/2], \[FormalCapitalX][x, 1, 1, Pi/2], \[FormalCapitalZ][z2, 1, 1, Pi/2], \[FormalCapitalW][i, z1], \[FormalCapitalW][z1, x], \[FormalCapitalW][x, z2], \[FormalCapitalW][z2, o]}]
Out[5]=
In[6]:=
diagram2["LabeledGraph"]
Out[6]=
In[7]:=
operator2 = ResourceFunction["ZXDiagramToQuantumDiscreteOperator"][diagram2]
Out[7]=
In[8]:=
operator2["Operator"]
Out[8]=

Convert a four-spider ZX-diagram (representing a controlled Hadamard gate) into an arity-2 discrete quantum operator:

In[9]:=
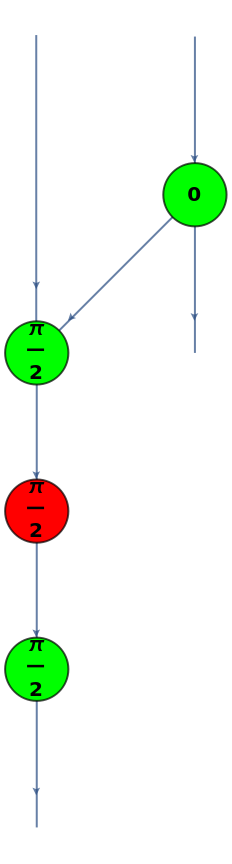
diagram = ResourceFunction[ "MakeZXDiagram"][{\[FormalCapitalZ][z1, 2, 2, Pi/2], \[FormalCapitalX][x, 2, 2, Pi/2], \[FormalCapitalZ][z2, 2, 2, Pi/2], \[FormalCapitalW][i1, z1], \[FormalCapitalW][z1, x], \[FormalCapitalW][x, z2], \[FormalCapitalW][z2, o1], \[FormalCapitalZ][z3, 2, 2, 0], \[FormalCapitalW][i2, z3], \[FormalCapitalW][z3, o2], \[FormalCapitalW][z3, z1]}]
Out[9]=
In[10]:=
LayeredGraphPlot[diagram["LabeledGraph"], {i1, i2} -> Automatic]
Out[10]=
In[11]:=
operator = ResourceFunction["ZXDiagramToQuantumDiscreteOperator"][diagram]
Out[11]=
In[12]:=
operator["Operator"]
Out[12]=

Convert a more complicated four-spider ZX-diagram (used representing complementary bases in the bialgebra simplification rule of the ZX-calculus) into an arity-2 discrete quantum operator:

In[13]:=
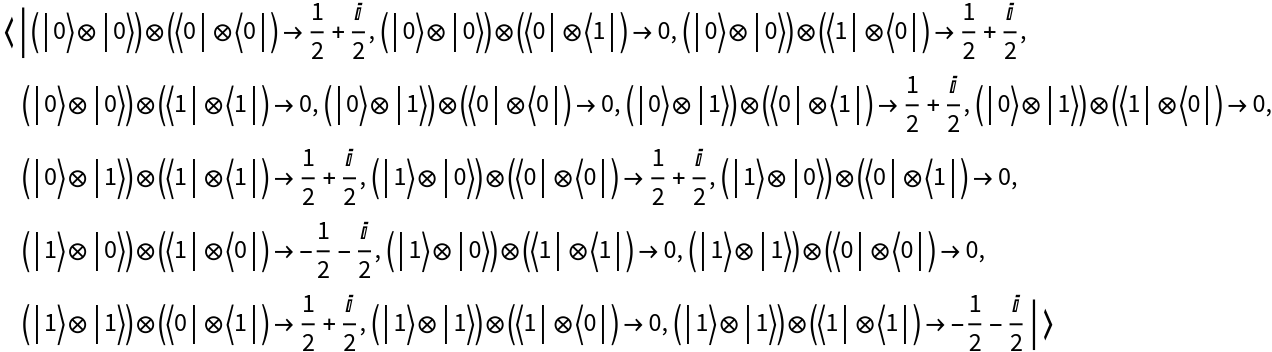
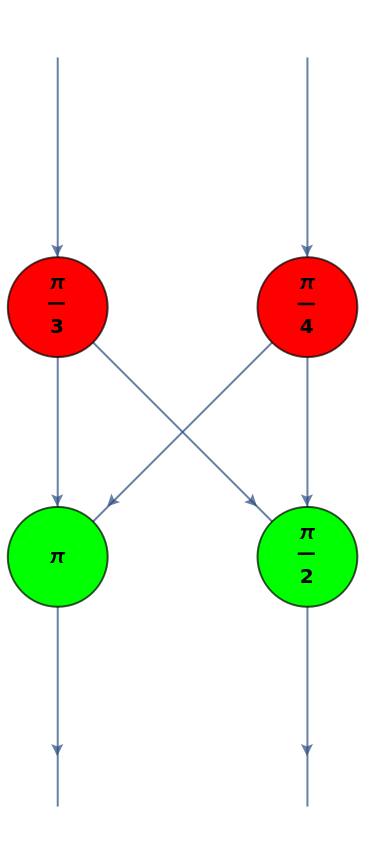
diagram2 = ResourceFunction[ "MakeZXDiagram"][{\[FormalCapitalZ][z1, 1, 1, Pi], \[FormalCapitalZ][z2, 1, 1, Pi/2], \[FormalCapitalX][x1, 1, 1, Pi/3], \[FormalCapitalX][x2, 1, 1, Pi/4], \[FormalCapitalW][i1, x1], \[FormalCapitalW][i2, x2], \[FormalCapitalW][x1, z1], \[FormalCapitalW][x1, z2], \[FormalCapitalW][x2, z1], \[FormalCapitalW][x2, z2], \[FormalCapitalW][z1, o1], \[FormalCapitalW][z2, o2]}]
Out[13]=
In[14]:=
LayeredGraphPlot[diagram2["LabeledGraph"], {i1, i2} -> Automatic]
Out[14]=
In[15]:=
operator2 = ResourceFunction["ZXDiagramToQuantumDiscreteOperator"][diagram2]
Out[15]=
In[16]:=
operator2["Operator"]
Out[16]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 08 June 2021

Source Metadata

  • Citation:
    • Bob Coecke and Ross Duncan (2011), "Interacting Quantum Observables: Categorical Algebra and Diagrammatics"
    • Jonathan Gorard, Manojna Namuduri and Xerxes Arsiwalla (2020), "ZX-Calculus and Extended Hypergraph Rewriting Systems I: A Multiway Approach to Categorical Quantum Information Theory"
    • Jonathan Gorard, Manojna Namuduri and Xerxes Arsiwalla (2021), "ZX-Calculus and Extended Wolfram Model Systems II: Fast Diagrammatic Reasoning with an Application to Quantum Circuit Simplification"

Related Resources

Author Notes

ZXDiagramToQuantumDiscreteOperator currently uses global symbols like z1 and x1. Local definition or values for those symbols can cause ZXDiagramToQuantumDiscreteOperator to have unexpected results.

License Information