Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the location of a signpost with given distances to a set of cities
ResourceFunction["WorldTravellerSignpostSolve"][{{loc1, dist1},{loc2, dist2},…}] given the locations loci and distances disti find the location of the signpost. |
Given a set of cities and their distance, what is the location of the signpost:
| In[1]:= | ![locs = {
{Entity["City", {"LosAngeles", "California", "UnitedStates"}], Quantity[9060, "Kilometers"]},
{Entity["City", {"NewYork", "NewYork", "UnitedStates"}], Quantity[6013, "Kilometers"]},
{Entity["City", {"Berlin", "Berlin", "Germany"}], Quantity[431, "Kilometers"]},
{Entity["City", {"Oslo", "Oslo", "Norway"}], Quantity[901, "Kilometers"]}
};
ResourceFunction[
"WorldTravellerSignpostSolve", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][locs]](https://www.wolframcloud.com/obj/resourcesystem/images/1a0/1a0b5659-eb5f-4f8b-8b74-c94c7778e91d/4f1a9e7174d3b330.png) |
| Out[2]= |
Numbers are interpreted as kilometers:
| In[3]:= | ![locs = {
{Entity["City", {"LosAngeles", "California", "UnitedStates"}], 9000},
{Entity["City", {"NewYork", "NewYork", "UnitedStates"}], 6000},
{Entity["City", {"Berlin", "Berlin", "Germany"}], Quantity[431, "Kilometers"]},
{Entity["City", {"Oslo", "Oslo", "Norway"}], Quantity[901, "Kilometers"]}
};
ResourceFunction[
"WorldTravellerSignpostSolve", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][locs]](https://www.wolframcloud.com/obj/resourcesystem/images/1a0/1a0b5659-eb5f-4f8b-8b74-c94c7778e91d/4e12d9845f6144cb.png) |
| Out[4]= |
Given the signpost, find the location:

| In[5]:= | ![locs = {
{Entity["Neighborhood", "Waikiki::Honolulu::Hawaii::UnitedStates"],
Quantity[9920, "Miles"]},
{Entity["Country", "SouthAfrica"], Quantity[2774, "Miles"]},
{Entity["City", {"HongKong", "HongKong", "HongKong"}], Quantity[4373, "Miles"]},
{Entity["Country", "Jamaica"], Quantity[9113, "Miles"]},
{Entity["City", {"Prague", "Prague", "CzechRepublic"}], Quantity[4542, "Miles"]},
{Entity["Country", "Barbados"], Quantity[7970, "Miles"]},
{Entity["City", {"NewYork", "NewYork", "UnitedStates"}], Quantity[8442, "Miles"]},
{Entity["AdministrativeDivision", {"California", "UnitedStates"}], Quantity[10189, "Miles"]},
{Entity["City", {"Prague", "Prague", "CzechRepublic"}], Quantity[4542, "Miles"]},
{Entity["City", {"Barcelona", "Barcelona", "Spain"}], Quantity[4626, "Miles"]}
};
loc = ResourceFunction[
"WorldTravellerSignpostSolve", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][locs]](https://www.wolframcloud.com/obj/resourcesystem/images/1a0/1a0b5659-eb5f-4f8b-8b74-c94c7778e91d/20add4151ebeb014.png) |
| Out[6]= |
Find the country:
| In[7]:= |
| Out[7]= |
Visualize the lines and the found minimum:
| In[8]:= |
Investigate the effect of the precision of the distances on the final location. Given a location, and some random cities, find the estimates for 'rounded' distances:
| In[9]:= | ![SeedRandom[1234];
p = GeoPosition[{16.78`, -3.01`}];
places = Table[RandomGeoPosition[], {15}];
dists = GeoDistance[p, #] & /@ places;
dists = QuantityMagnitude[#, "Kilometers"] & /@ dists;
poss = Table[{a, ResourceFunction[
"WorldTravellerSignpostSolve", ResourceSystemBase -> "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"][{places, Round[dists, a]} // Transpose]}, {a, {0.1, 0.3, 1, 3, 10, 30, 100, 300, 1000}}]](https://www.wolframcloud.com/obj/resourcesystem/images/1a0/1a0b5659-eb5f-4f8b-8b74-c94c7778e91d/7ffb987b30bb761a.png) |
| Out[14]= |  |
Plot the error in the location as a function of the rounding:
| In[15]:= | ![ListLogLogPlot[{poss[[All, 1]], QuantityMagnitude[GeoDistance[p, #], "Kilometers"] & /@ poss[[All, 2]]} // Transpose, FrameLabel -> {"Rounding in distances [m]", "Error in location [m]"},
Frame -> True
]](https://www.wolframcloud.com/obj/resourcesystem/images/1a0/1a0b5659-eb5f-4f8b-8b74-c94c7778e91d/40bfeaf4e06a1ff3.png) |
| Out[15]= | 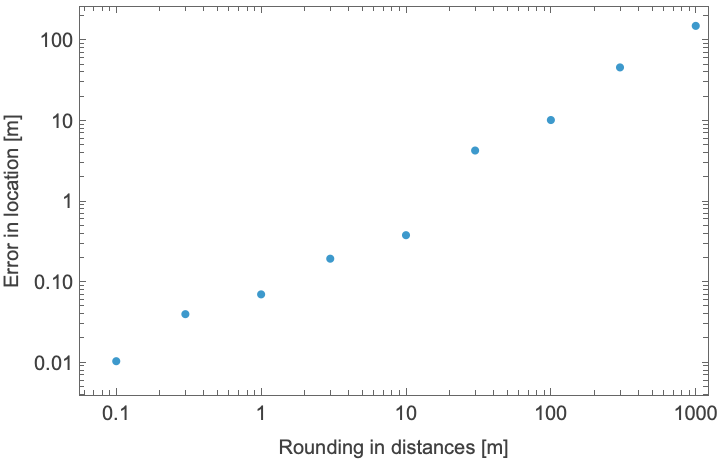 |
We see that the error in the location is much better than the errors introduced by rounding.
Wolfram Language 13.0 (December 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License