Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute projections of the Wolfram–Ricci curvature tensor of a graph and many associated properties
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,vin,vout] computes the projection of the Wolfram–Ricci curvature tensor from vertex vin to vertex vout in a graph graph of dimension dim, with an automatically-computed maximum tube radius. | |
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,vin,vout,rad] uses maximum tube radius rad. | |
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,vin,vout,{radmin,radmax}] uses minimum tube radius radmin and maximum tube radius radmax. | |
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,v,All] gives an Association showing the projections of the Wolfram–Ricci curvature tensor from vertex v to each vertex in a graph graph of dimension dim, with an automatically-computed maximum tube radius. | |
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,v,All,rad] uses maximum tube radius rad. | |
ResourceFunction["WolframRicciCurvatureTensor"][graph,dim,v,All,{radmin,radmax}] uses minimum tube radius radmin and maximum tube radius radmax. | |
ResourceFunction["WolframRicciCurvatureTensor"][…,"prop"] gives the property "prop" for the specified Wolfram–Ricci curvature tensor computation. |
| "BallVolume" | the volumes of geodesic balls of various radi around a given vertex |
| "AllBallVolumes" | an association showing the volumes of geodesic balls of various radii around each vertex |
| "ScalarCurvature" | the Wolfram–Ricci scalar curvatures at a given vertex |
| "AllScalarCurvatures" | an association showing the Wolfram–Ricci scalar curvatures at each vertex |
| "ScalarHighlightedGraph" | a highlighted graph showing how the Wolfram–Ricci scalar curvature is computed |
| "TubeVolume" | the volumes of geodesic tubes of various radii between two given vertices |
| "AllTubeProjectionVolumes" | an association showing the volumes of geodesic tubes of various volumes between a given vertex and all other vertices |
| "Curvature" | the projection of the Wolfram–Ricci curvature tensor between two given vertices |
| "AllCurvatureProjections" | an association showing the projections of the Wolfram–Ricci curvature tensor between a given vertex and all other vertices |
| "HighlightedGraph" | a highlighted graph showing how the projection of the Wolfram–Ricci curvature tensor is computed |
| "TransitivelyReduce" | False | whether to use the transitive reduction of the input graph |
| "UndirectedGraph" | False | whether to use the undirected form of the input graph |
| "VolumeMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls of different volumes (or simply return all values) |
| "CurvatureMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls yielding different curvatures (or simply return all values) |
| "VertexMethod" | Identity | whether to take a maximum, minimum or mean over all vertices in the input graph (or simply return all values) |
Compute the projection of the Wolfram–Ricci curvature tensor between vertices 145 and 355 in a 20-by-20 2-dimensional grid graph:
| In[1]:= |
|
| Out[1]= |

|
| In[2]:= |
|
| Out[2]= |
|
Compute the maximum and minimum projections of the curvature tensor over geodesic tubes with radii up to 4:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
Return a list of all projections of the curvature tensor over geodesic tubes with radii up to 4:
| In[5]:= |
|
| Out[5]= |
|
Show the geodesic tubes with radii up to 4 as a highlighted graph:
| In[6]:= |
|
| Out[6]= |
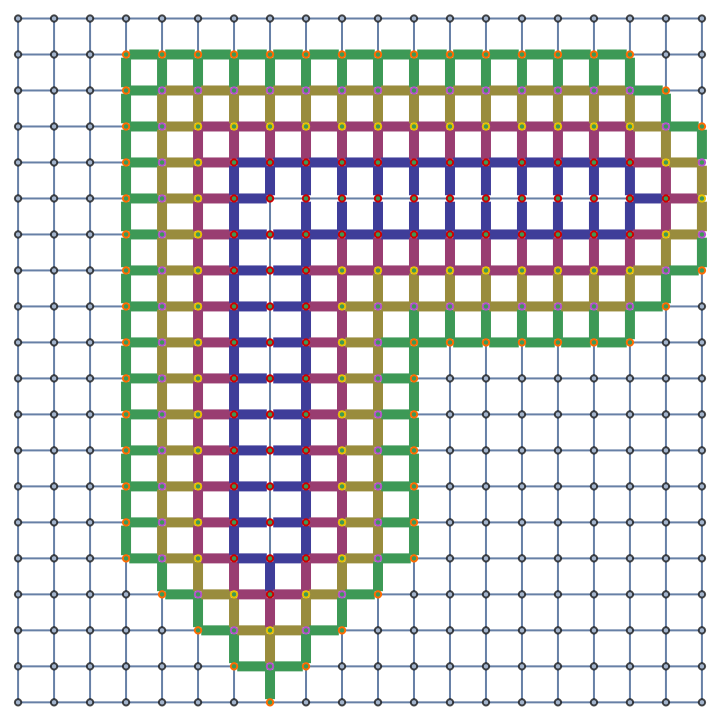
|
Return an Association showing the projections of the Wolfram–Ricci curvature tensor between vertex 145 and each vertex in the graph, over geodesic tubes with radii up to 4:
| In[7]:= |
![Take[ResourceFunction["WolframRicciCurvatureTensor"][gridGraph, 2, 145, All, 4, "AllCurvatureProjections"], 50]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/3ab5ce8fff56ba28.png)
|
| Out[7]= |

|
Compute the maximum and minimum projections of the curvature tensor across all vertices:
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
Compute the average projection of the curvature tensor across all vertices:
| In[10]:= |
|
| Out[10]= |
|
Compute the average volume of geodesic tubes between vertices 145 and 855 in a 10-by-10-by-10 3-dimensional grid graph:
| In[11]:= |
|
| Out[11]= |

|
| In[12]:= |
|
| Out[12]= |
|
Compute the maximum and minimum volumes of geodesic tubes with radii between 2 and 4:
| In[13]:= |
|
| Out[13]= |
|
| In[14]:= |
|
| Out[14]= |
|
Return a list of all volumes of geodesic tubes with radii between 2 and 4:
| In[15]:= |
|
| Out[15]= |
|
Show the geodesic tubes with radii between 2 and 4 as a highlighted graph:
| In[16]:= |
|
| Out[16]= |
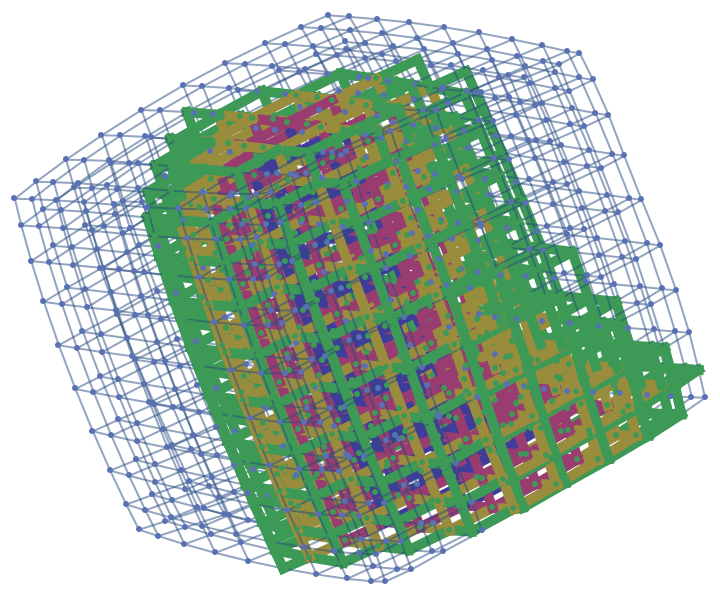
|
Return an Association showing the geodesic tube volumes between vertex 145 and each vertex in the graph, with radii up to 3:
| In[17]:= |
![Take[ResourceFunction["WolframRicciCurvatureTensor"][gridGraph, 3, 145, All, 3, "AllTubeProjectionVolumes"], 50]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/60466dac37537666.png)
|
| Out[17]= |

|
Compute the maximum and minimum tube volumes between vertex 145 and each vertex in the graph, with radii up to 3:
| In[18]:= |
|
| Out[18]= |
|
| In[19]:= |
|
| Out[19]= |
|
Compute the projection of the Wolfram–Ricci curvature tensor between two arbitrary vertices in an approximately spherical graph (produced using the resource function ExtrinsicCurvedManifoldToGraph) and show that the projection is positive:
| In[20]:= |
![sphereGraph = \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"], {Null, CompressedData["
1:eJwVxfk/GgoAAHDRXJFjrrAOaRmhJIVHZJGtVzRnLKPcSZR1keN55RoKKSJX
GipRMoqaYv6s93nfX76InlFWT2hISAg6LCTk/wd2ssYiByJ3opAY7JgOKc7o
yToYO4jUancyGrMao3KRuZsW2HieETIB0eafZPRn9Tf2J0AStAk7sOfxZ1hg
PJCwl7+Xi8fgsXgABoAF4JtEkPmJ+Sa9SA9gYVhYFp7V8AIpL58on+81gtgq
E0jKlmY8Nj72PP5zqbo0XUamJ6Sna9N3QGAwGyx9Y8l7Nb4+vp5cg1cgK+Ur
EyvzK6gilCmnN8eIGhoytc21XWUfZF/lCPIEvQKBUfAseA0rD/ua39EhRp0V
nanOTGfruvXH9deIzQhLYgOMTB4nr5N15GeQHCxny6XyMZfOdeBCuYvcKrfJ
feZuW5xbXLyCUclU6jhVR3VRAyBboq3BJrfZXiIRCAxiIOeo98h4BGKCmYlM
JpspZcqZtsy8zIbMnszHzJewWkhteW3tRO08wIPwYDxYD97D8oDMYDPTzDZL
zXJzTF5Mb4wgxhi5n7Cfvj+wr93f2Uf9/PEzcTBzsGFw0Barir1sn2s/ab9G
FRQUFZwVuJuCoqA+CPOT/VT/uF/nd/n9gZianJq8mpreGkGNseY10Zfpa/D1
+AZ9Np/vJX2bvS3d1m5vm2MXVAsLpoXLBXf+TcfN3s3JDZlCoVLGKOsUHcVF
8X+/WLy4uEpGJGOSB5LFCd353R3d3XvdN9nV1dRqUbWr2p/2Ka0jTRx5m36L
uB241d7u3O7fRrUgW3JbYqZzpvOma6Z7pwXT08bpVxAXzOVOcKVcOXeeu8I1
vzmOON48PrYkCxFCpBAjbBEOCIVi8iRlkjrZONk/OTY5uT6pm3RFKZCKXAVG
gVe0KISKtCpkVZU4CZVUkFSUpEo6S3K/+wYgfCBgCXgCgfXu82fmZ/bnbxm7
jbtfd3t2+3dj6+oW3v6GEYlkIoVIJY4TdUQ/MUB8fltc/L34N0xNVJPVFDVV
Pa5Wr6t1ar86oH4Ok0Fk5bJa2YRMNi/bA9CwNDyNQKOxaJ6osrQyZFlZVVlL
mTh/uH14+GT4Jm0NuVa2VrX2aU28llNS0lvyo+So5DmrtLS/dKz0oEkpUir1
yoAyGJ4cjgjHhA+EC8PFaXf5d5/uOu6674bv9u5u7gBQKAKaC8VAsVA8lAZl
QYVQBdSTfd52Pne+eH5+hdoY2tgwweBwIrwaToFT4SK4Eq6Gu+B+eCAiNfW4
qbV1qHWjVd8ajNhK3WobHT0YPR+9hkngEqJEJJEoJXpJQBKEaMo1tRquZkIj
08xrVjQAL9SL8GK8WC/eS/OyvB7vu9Nvp6eWhubmnmZf80tsX11f30LfZZIB
ZSgwFBmGDCrDhsFgMpwZ3KH5oe2hw6EnodehN6F3f239ddR02HooOpQcKg/1
h4fBwtbCocJ/ClWFC4UbhabCSwAOisPgsDgcHkfA0XAsnAfnhTurnVSnyClx
Kp16p9Pl9EetIldzV8tWW1YVq4CUFGwKLoWQQkthgdBgdCIa3YBuRg+ipWg5
2ob2oV8i4uNT4zfjt+KP4y1dm12nXZbQ+vq2+vb60fq5+vP6ayAImAhEA5lA
NnAQKAXKgTYQD8xj87g8npQn563wtnnmt7+Kf/36HeVIcyAdZY4qR4tD6BA7
FI5Vx5ojGhX9I3oj+mf4fcJ98j3ifuBeeL9zv39/e59kR9kL7IX2IrvKvmA3
2E32M7vdDSPBSaQmkogkISlJetIhKUAK/v1v7MiHkdyRupG+kQhGPCOVwehi
bDK2GMcMS9hM/kztjGxmZm/m5tOfuT+//+Q8lDz0Pvx4eHgGxsXExSXGDcb9
G2eL/Phx++NtRmdWZ2lnY2fn187+zt3op9Qn1FPBU9HT1pPh6edTQiWkMr2y
srtSVqmt3Kvcj5iKn2JMdU1NbU5Z4PxsfjWfyueL+BK+ku/ku/j+iIr4igpG
RVfFVMVmxXHFaYUlxpppzbPWWAXWaavRan20vgKW3iylLH1YIizRloCzcbOJ
s+jZhtnB2VnbrC+bXk2nN9H5dBFdT7+gO+lBEAfMQXOaORwuh8eZ4Eg5cs48
Z4Wj4Zg5L2+/FH/58it2+cMyYblueWT5Pf399/cX/wHrgXhh
"]}, {EdgeStyle -> {
Directive[
Hue[0.63, 0.7, 0.5],
Opacity[0.7]]}, VertexStyle -> {
Directive[
Hue[0.63, 0.26, 0.89],
EdgeForm[
Directive[
Hue[0.63, 0.7, 0.33],
Opacity[0.95]]]]}, VertexCoordinates -> CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"], {
{Hue[0.63, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxfk/GgoAAHDRXJFjrrAOaRmhJIVHZJGtVzRnLKPcSZR1keN55RoKKSJX
GipRMoqaYv6s93nfX76InlFWT2hISAg6LCTk/wEpACgAA8ACcAA8gACgAViA
JYAH4A3ND60PbQ8dDj0JvQ69Cb0LKw+rDfsaJgubAYKAccBEIBrIBLKBg0Ap
UA6cBdreLL05fmMJTw5HhGPCB8KF4eLw+4j4iNSIighGxFTEZsRWxHGEJTI9
EhH5MXIgUhu5E7kfeRuFjMqNKotqiVJErUY5olHRP6I3on9GP4HAIDSICWKD
OCAuiAeSguQgM8gWExeTF1MT0xsjiJmOMcZYY+ti+2JHYlWxC7HLsZdgNJgJ
ZoM5YC6YB5aC5eAVsDkuMW4wbjbu3zhbfGp8RTwjfip+M34r/jjekgBJSE+o
TOhO0CbsJOwl7CfcJ6ITmYkNiYOJs4m2RN/b4rdf3v56+zsJlVSQVJSkSjIk
nSXZk9zJiGRM8kCyMFmcfJ+CTcGlEFJoKayUpVRG6lbqcepTWllaVdqntI40
cdpamiPtDlIOqYTUQiYgMsg8ZAWigWjTK9O16dvpO+n76bcZjRmdGT0Z/Rm7
GY+ZeZkNmT2Zg5nWzMdMX+bLu8/vvr07hSKguVAMFAvFQfFQGpQFFUIVUA/U
C4PDiDASjAyjwsZhEpga5ocFYM9wIpwEr4ZT4FQ4Hy6CS+BKuBruhLvgfngA
gUEMIISIW8Q9woPwZpVmNWZ1ZvVnjWUdIHORZcgqZAtSiBQjFchV5BrSkV2d
Tc/mZx9kn2dfoQpQRagh1AbKgDKhfqLOUHaUG/X0nv7++/sLdAO6Gc1BD6Kl
aDl6Fm1D+9AvOSU5NTm9OYKc6RxjzlHOwwfCh5EPSx+Wc/G5LbkjuYrc1bya
PEHedJ4xz5r3isFicBg8hoURYhQYD8ab35HfnT+cP5O/l3+Sf5N/V1BUYCg4
K7AXuAueClsLhwr/KVQVLhRuFJoK7YWXWBwWjyVgaVgW1oP14vA4Ao6GY+E8
OG+RoeisyF7kLnrCE/A0PAuvwHvw3uIvxd+LfxX/JtAILMISYbmkt+RHyVHJ
Q8kzkUykEKnEcaKEqCbqiH5igPhMaiKJSBKSkqQnHZICpGBpZ2l/6VjpQVlV
WUuZuGy1bK3MUV5bPlEuK58vXynX/LX111EFo6KrYqpis+K44rTCUtldKavU
Vu5V7pMpZCp5nDxJVpPXyTqyn/xcJa5aq3JUU6vp1fxqUbWz2lXtp1ApY5RJ
ipqyTtFRXBR/TW+NoGa6xlhjrXn9uP3xlsqnjlMnqWqqjuqkuqh+aqB2olZW
O1M7X6up66sbqVuoW6axaEs0D81b31bfXj9aP1d/Xn/9ae3T3ac/n5mf2Z+/
0ZvofLqIrqdf0J304N//MroYU4xNxhbjmGFhsplSppxpZtoamhsGG2YbbA2+
hpfGzsb+xsnG3cZHlofl/fKrqbVJ1KRs0jcdNgWbOc09zb7mlxZhi6JltcXR
OtS60apvPWwNto22zbUttp23XbUPt8+1n7Rfs3lsKVvO3mabO7o7xB03HXed
Xzv7O3e/7nK4HB5ngiPlyDnznBWOhmPmvHRNdW12nXZZvp1273XfdN/17PY8
9vi4PO4EV8qVc+e5K1wN18yT8uS8Fd42z9wr6J3uNfYe9T70jfQt9F32T/bv
DggHdgb2B24H7gdnB22DvqGNIcOQafhk+Gb4ji/iS/hKvpPv4vtHlgXTAqPA
KngWvI4ejJ6PXgvFQoXQIbwfmxzTjR2MucbV4/7xwPizSCJSivSiQ5FTFBSv
iR0Tson5iZUJzfcLiVKilxxKnJKAJCiVS7elZtmMbF6mke3JzXKbYlXhmFyf
1E26pjanLEq98lDpVAaUwWnjtHX6dWZv5mbWNuubW5w7n/vzz+X8yrxGtaAy
qEyqM5Vddalyq9fVOrVfHVA/L5gW7AuXC+7F88WLxasVzY+fPx5WHWuOdd36
4/qrdlu7o93X3m4YNkybx5uWrSedS+ffNusP9U590GAynBnsBrfhaWd/53bn
3nhktBpf92727vZv9+9NZya76dLkPnAdBo8tJ9cnN6eWn09n9jP3+dXFlfXR
+mrz2V7sbqfL6Xf5b+5u73/99ngfnh9ffS/+wO8//wGov3hh
"]], 0.04512775258949886]},
{Hue[0.63, 0.26, 0.89], EdgeForm[{Hue[0.63, 0.7, 0.33], Opacity[
0.95]}], SphereBox[1, 0.04512775258949886], SphereBox[2, 0.04512775258949886], SphereBox[3, 0.04512775258949886], SphereBox[4, 0.04512775258949886], SphereBox[5, 0.04512775258949886], SphereBox[6, 0.04512775258949886], SphereBox[7, 0.04512775258949886], SphereBox[8, 0.04512775258949886], SphereBox[9, 0.04512775258949886], SphereBox[10, 0.04512775258949886], SphereBox[11, 0.04512775258949886], SphereBox[12, 0.04512775258949886], SphereBox[13, 0.04512775258949886], SphereBox[14, 0.04512775258949886], SphereBox[15, 0.04512775258949886], SphereBox[16, 0.04512775258949886], SphereBox[17, 0.04512775258949886], SphereBox[18, 0.04512775258949886], SphereBox[19, 0.04512775258949886], SphereBox[20, 0.04512775258949886], SphereBox[21, 0.04512775258949886], SphereBox[22, 0.04512775258949886], SphereBox[23, 0.04512775258949886], SphereBox[24, 0.04512775258949886], SphereBox[25, 0.04512775258949886], SphereBox[26, 0.04512775258949886], SphereBox[27, 0.04512775258949886], SphereBox[28, 0.04512775258949886], SphereBox[29, 0.04512775258949886], SphereBox[30, 0.04512775258949886], SphereBox[31, 0.04512775258949886], SphereBox[32, 0.04512775258949886], SphereBox[33, 0.04512775258949886], SphereBox[34, 0.04512775258949886], SphereBox[35, 0.04512775258949886], SphereBox[36, 0.04512775258949886], SphereBox[37, 0.04512775258949886], SphereBox[38, 0.04512775258949886], SphereBox[39, 0.04512775258949886], SphereBox[40, 0.04512775258949886], SphereBox[41, 0.04512775258949886], SphereBox[42, 0.04512775258949886], SphereBox[43, 0.04512775258949886], SphereBox[44, 0.04512775258949886], SphereBox[45, 0.04512775258949886], SphereBox[46, 0.04512775258949886], SphereBox[47, 0.04512775258949886], SphereBox[48, 0.04512775258949886], SphereBox[49, 0.04512775258949886], SphereBox[50, 0.04512775258949886], SphereBox[51, 0.04512775258949886], SphereBox[52, 0.04512775258949886], SphereBox[53, 0.04512775258949886], SphereBox[54, 0.04512775258949886], SphereBox[55, 0.04512775258949886], SphereBox[56, 0.04512775258949886], SphereBox[57, 0.04512775258949886], SphereBox[58, 0.04512775258949886], SphereBox[59, 0.04512775258949886], SphereBox[60, 0.04512775258949886], SphereBox[61, 0.04512775258949886], SphereBox[62, 0.04512775258949886], SphereBox[63, 0.04512775258949886], SphereBox[64, 0.04512775258949886], SphereBox[65, 0.04512775258949886], SphereBox[66, 0.04512775258949886], SphereBox[67, 0.04512775258949886], SphereBox[68, 0.04512775258949886], SphereBox[69, 0.04512775258949886], SphereBox[70, 0.04512775258949886], SphereBox[71, 0.04512775258949886], SphereBox[72, 0.04512775258949886], SphereBox[73, 0.04512775258949886], SphereBox[74, 0.04512775258949886], SphereBox[75, 0.04512775258949886], SphereBox[76, 0.04512775258949886], SphereBox[77, 0.04512775258949886], SphereBox[78, 0.04512775258949886], SphereBox[79, 0.04512775258949886], SphereBox[80, 0.04512775258949886], SphereBox[81, 0.04512775258949886], SphereBox[82, 0.04512775258949886], SphereBox[83, 0.04512775258949886], SphereBox[84, 0.04512775258949886], SphereBox[85, 0.04512775258949886], SphereBox[86, 0.04512775258949886], SphereBox[87, 0.04512775258949886], SphereBox[88, 0.04512775258949886], SphereBox[89, 0.04512775258949886], SphereBox[90, 0.04512775258949886], SphereBox[91, 0.04512775258949886], SphereBox[92, 0.04512775258949886], SphereBox[93, 0.04512775258949886], SphereBox[94, 0.04512775258949886], SphereBox[95, 0.04512775258949886], SphereBox[96, 0.04512775258949886], SphereBox[97, 0.04512775258949886], SphereBox[98, 0.04512775258949886], SphereBox[99, 0.04512775258949886], SphereBox[100, 0.04512775258949886], SphereBox[101, 0.04512775258949886], SphereBox[102, 0.04512775258949886], SphereBox[103, 0.04512775258949886], SphereBox[104, 0.04512775258949886], SphereBox[105, 0.04512775258949886], SphereBox[106, 0.04512775258949886], SphereBox[107, 0.04512775258949886], SphereBox[108, 0.04512775258949886], SphereBox[109, 0.04512775258949886], SphereBox[110, 0.04512775258949886], SphereBox[111, 0.04512775258949886], SphereBox[112, 0.04512775258949886], SphereBox[113, 0.04512775258949886], SphereBox[114, 0.04512775258949886], SphereBox[115, 0.04512775258949886], SphereBox[116, 0.04512775258949886], SphereBox[117, 0.04512775258949886], SphereBox[118, 0.04512775258949886], SphereBox[119, 0.04512775258949886], SphereBox[120, 0.04512775258949886], SphereBox[121, 0.04512775258949886], SphereBox[122, 0.04512775258949886], SphereBox[123, 0.04512775258949886], SphereBox[124, 0.04512775258949886], SphereBox[125, 0.04512775258949886], SphereBox[126, 0.04512775258949886], SphereBox[127, 0.04512775258949886], SphereBox[128, 0.04512775258949886], SphereBox[129, 0.04512775258949886], SphereBox[130, 0.04512775258949886], SphereBox[131, 0.04512775258949886], SphereBox[132, 0.04512775258949886], SphereBox[133, 0.04512775258949886], SphereBox[134, 0.04512775258949886], SphereBox[135, 0.04512775258949886], SphereBox[136, 0.04512775258949886], SphereBox[137, 0.04512775258949886], SphereBox[138, 0.04512775258949886], SphereBox[139, 0.04512775258949886], SphereBox[140, 0.04512775258949886], SphereBox[141, 0.04512775258949886], SphereBox[142, 0.04512775258949886], SphereBox[143, 0.04512775258949886], SphereBox[144, 0.04512775258949886], SphereBox[145, 0.04512775258949886], SphereBox[146, 0.04512775258949886], SphereBox[147, 0.04512775258949886], SphereBox[148, 0.04512775258949886], SphereBox[149, 0.04512775258949886], SphereBox[150, 0.04512775258949886], SphereBox[151, 0.04512775258949886], SphereBox[152, 0.04512775258949886], SphereBox[153, 0.04512775258949886], SphereBox[154, 0.04512775258949886], SphereBox[155, 0.04512775258949886], SphereBox[156, 0.04512775258949886], SphereBox[157, 0.04512775258949886], SphereBox[158, 0.04512775258949886], SphereBox[159, 0.04512775258949886], SphereBox[160, 0.04512775258949886], SphereBox[161, 0.04512775258949886], SphereBox[162, 0.04512775258949886], SphereBox[163, 0.04512775258949886], SphereBox[164, 0.04512775258949886], SphereBox[165, 0.04512775258949886], SphereBox[166, 0.04512775258949886], SphereBox[167, 0.04512775258949886], SphereBox[168, 0.04512775258949886], SphereBox[169, 0.04512775258949886], SphereBox[170, 0.04512775258949886], SphereBox[171, 0.04512775258949886], SphereBox[172, 0.04512775258949886], SphereBox[173, 0.04512775258949886], SphereBox[174, 0.04512775258949886], SphereBox[175, 0.04512775258949886], SphereBox[176, 0.04512775258949886], SphereBox[177, 0.04512775258949886], SphereBox[178, 0.04512775258949886], SphereBox[179, 0.04512775258949886], SphereBox[180, 0.04512775258949886], SphereBox[181, 0.04512775258949886], SphereBox[182, 0.04512775258949886], SphereBox[183, 0.04512775258949886], SphereBox[184, 0.04512775258949886], SphereBox[185, 0.04512775258949886], SphereBox[186, 0.04512775258949886], SphereBox[187, 0.04512775258949886], SphereBox[188, 0.04512775258949886], SphereBox[189, 0.04512775258949886], SphereBox[190, 0.04512775258949886], SphereBox[191, 0.04512775258949886], SphereBox[192, 0.04512775258949886], SphereBox[193, 0.04512775258949886], SphereBox[194, 0.04512775258949886], SphereBox[195, 0.04512775258949886], SphereBox[196, 0.04512775258949886], SphereBox[197, 0.04512775258949886], SphereBox[198, 0.04512775258949886], SphereBox[199, 0.04512775258949886], SphereBox[200, 0.04512775258949886]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
ImageSize->{320.3671875, Automatic},
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/77743a428b09c16d.png)
|
| In[21]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][sphereGraph, 2, \
{0.06448108156822731`, -0.8531712722406339`, 0.5146821808082329`}, {0.23499005420178715`, -0.48812613069710237`, 0.8391248174833306`}]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/598a07631465cee9.png)
|
| Out[21]= |
|
Show the geodesic tubes with radii up to 2 as a highlighted graph:
| In[22]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][sphereGraph, 2, \
{0.06448108156822731`, -0.8531712722406339`, 0.5146821808082329`}, {0.23499005420178715`, -0.48812613069710237`, 0.8391248174833306`}, 2, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/70195d5001cce003.png)
|
| Out[22]= |
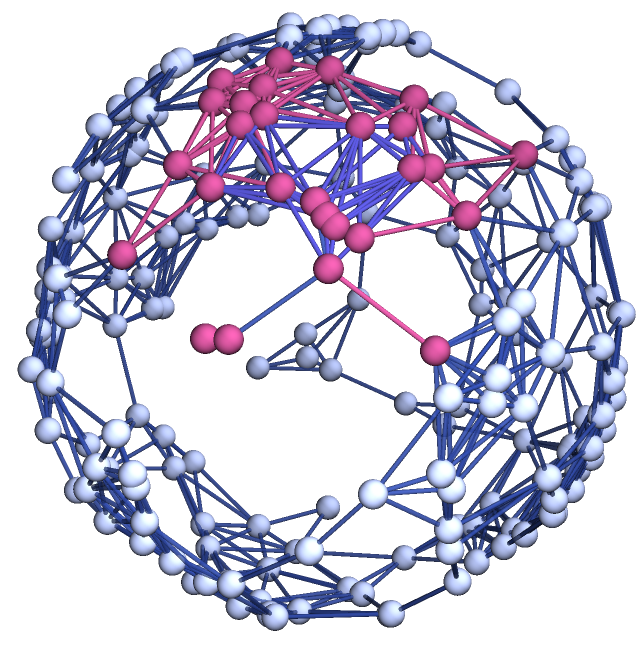
|
Compute the projection of the Wolfram–Ricci curvature tensor between two arbitrary vertices in an approximately hyperbolic paraboloidal graph (produced using the resource function ExtrinsicCurvedManifoldToGraph) and show that the projection is negative:
| In[23]:= |
![saddleGraph = \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"], {Null, CompressedData["
1:eJwVxfk/Gg4DAODvEjmGcktsUo7lzLHSNCpCSZRJUqQYJUdzRJdSjgxLOWoS
uUWInNNY6M96P+/zy5PK72/kA/7777+FoP/++/9IRdgbvDG6vX0vLC/vDY5C
NUZvRnuQHoUnLCIiL+ItMDqwPXAv0AMIA0QA8gBvcGlgWXRZ2WbIW/8fIBKo
AHrgEokUKEPKimQyhcwDJYV8Cykv/1b+1jAKNZKMkiXpUlJD0mj0eNn4+CZ8
RbIiXVlaATKZTUwp3IlyNjolTjqT3kQfBYxEjBSTQvbD9iP28/bL9/ff4GvM
NcmadC0Jg6FjGjBMjBSzhFnrv7j4A6gKq4qoyquqGoF2dRmBucjcXGauLFeR
NIQZahgaWgr89Kn90x6wBlmTW1NzEbgbvVu2O767uQsVCLoEMoFCYBTsCTz0
NmZbUxvcj/I3+p1++nHTcdsxVF+kF+i79DK93hhyl3pXfvftLiQlJTWlPOVb
yh10InViwojh0/lMPl/Cl/KX+Cv8teDiYFLwHtRQZOgy6A0Go+EOiEPicnG4
GpwMp8B5YqGxxbGk2IlYI1CXqyvS0XVNujadTKc7Rvbiemt6e/t7L4KrY6uL
q0nV8HvUfeO98/7eDzxCHuUe4Y5qjphHsiPd0dpRMB6Kx5PwAnwXXoE34vci
eyP7Iy8i/8RaoBa8hWSptggsXZYJi95isBgtIYUphamFheWF3wrvIs9rznvP
+8/PL87/YKb505LpoWnp9PTS9EpSBaaioqGCXzFUIa2YBqyHrUesV62PrANN
uSa8SWDqMslMCpPeZPIEL+IXSYuCxcW9otmm2bZZ3ezsMSo/vzHfmX+f/yff
/y72XfE70rvq9/9G/yV9/NjwcRTqKHIIHF0OmUPh0Dn0DoPD6DA5AIlhiRGJ
iXmJVYnrifuJb7EDxQPVAwMTwdefrvHXpOvF673rr5KvQ1+nvy59XYFjUdh8
LLYG24hdwzqx91g/dKZoRjDTNaOfmTHMGGdMM5YZB5yAIuQTsARCI0FCWCE4
CfcEPyA+LD4+L74ovim+LV4XPxt//Pnr54rPQ5+nPy99XoklQ8kkMrma3EUe
IE+Q9eQZsoFsJFuAz8jn3Gfcc81z77PsWfF89Ox5DryJvim7Gb/ZvNm9iVcX
qdvUMrVap9arZ9SzapPaEZYTn5OYk5OXU5RTnrOf8wZ/QD3kP2AfCA+ND86H
+4cHfyYqMz8Tm9mY2Z/pzDzPvMi8z3zI/JPpD7uKv0q8yrnKuyq6Kr/av7p6
i94o2xjf2Njc2N24AWRkVGWM0JuZzU3NzW3No8265tnmY6AIKcoV4UQCkUgm
UohMIo/oOSUtNS2tMI2cNpFmSLsDLGcsVy2PLL//+fMfkIfk5fJwPDyPJ+CJ
eDKegqfnmXgOnof3HHuWepZ2Rj4bOJs4M5wZzyxn0Ydlh72H44cbh5uHu4eH
N8EdnzrwHbyO9o4OQYeiY7Fjr8PTcQ3UIrW5Wpy2RsvTirQyrUKr1WlN2iOt
R/sc2dPT29Pfc95zEcjAMxg8RjujgyFgiBgKxiLDxNhjeBjX0adlp+OnG6eb
p7unh6enN+9///z9+1/S4OdBzGDFYMMgf3BwaHA68Db6tuy2/Xb8duN283b3
9vD29NZze3P7+e/Xv5K/Q3+n/y79XfkbP5UzlTdVNNU2pZ6a0k3pp2anHFNX
SUqMskJJVzYomUq+clApVSqnlWvwyq+VhMpKSeV05VLlSuXfkOTE5OSc5PLk
b8n7yVfJbynZqdlp2dmF2RPZhuyz7Lt3fcF9xX34PlJfdV9HX99i3zUQDIaC
c8FFYDyYAeaBBeAusAgsAyvAarAWrAPrwTNgA9gINoEdkZpoDVKD0/RoejXj
Gs2GZlOzqznUnGo8mhvNLZyaSUVR86lYKoFaQ6U2Up3Uc+oF9Z76QP1D9cc/
JT/lPOU9FT2pn6ae9E+zT46nq6ent/cfPvz88PvDvyQYDAOrgNFhDTAmrAnW
DOPDBmFS2ChMCVsLrI2uLautba8dr9XUbtRu1u7WHtae1t7U3qbMpc6lzWXP
Fc6Vz32bm5mbM8zdAc1gM9Kca8aZmeYmc7O5zcwzi8wys8KsNmvNOrPJbD4y
H5ufgTQwDUnLpeFoeBqNQePROmgCmogmoyloWpqeZqKZaQ6aJ5Qe2hTaHNoW
Oho6G3oM5IK5SG4uF8elcbk8roAr4sq4Cq6aq+XquCaumevgHnE93OdwaHha
eHZ4UTg5vCtcHa4PnwmfCzeEG8Mt4Y7wu/AnuBAlzBdihQRhpZAqbBQKJUKp
cEW4JnQK74UPQj94OH64aLhpuG2YOzwsG1YPTw3rhvXDs8OmYfOwY/h4+Clk
NXw1eTVlNW01ezVntXC1fPXb6tyqYXX1avVu9Qm2hdmq2KJvMbeatpq3+FvS
LeXW2tbW0TtbsC3WBrUV2/A2ko1sq7Z12fpsA7YJ24zNYFu0GW0WW3R9WX1t
fX1v/Xi9pn6jfrN+t/6w/rT+pv428lfPr/5f479+bf46/HWa5Ia5P7ox7go3
3d3g5rsH3UNuqXvUrXRvuaNjYnAxZTG1MfUxvTHjMZqYjZjNmN2Yw5jTGE/M
TcwtkBXKimflsugsJquJ1cxitbG4rGGWjKVm6VizLDNri3XEOg78Ef3j04/a
H+0/fuz9uAV0hnVGdCZ25nVWdXaOdK537ne+vcsKzorNgmZlFWeRsshZ1Vl9
WYtZxixLli3rOukSdvnxEnNZcdlwOXg5dDl6qbx0X4Ye0A+aDpoPWAdtB6MH
swcHxwB0GDoCHY9ORGegc9B5aHQVuhM9gl5Gr6Pfkl4+v2Bevr5UvDS8DL4M
vUy/uF8uX0DRoBgQDlQGqgXVg3pAvaBxkAa0AdoE7YIOQaegG9AtnIgi5hOx
RAKRWEmkEhuJQqKEKCWuENeITuI98YHoD/XCvBgv3cv0NnmbvSxvm5fvHfUq
vTrvmnfLe+A98h573d53QUGxQVlBxUGkIHJQddBA0ESQLRgChkCgEDyEBKFB
GBAepAMigHRB+iAKyCLECDFBLBAbZA9yDZwETUZOIidxkzWT1Mmeyd7JSc3k
+eTF5HPo9vvtD9v07abt5u3R7Z/bv7e3D7aPt73b/wLZIHY0O4aNZOPYtWwa
u57NYLN5bBFbwdawtexd9iHbw75h37Kf4RwUB8shcIicSg6Tw+FzhBwJR8pR
cpY4K5w1zhbHyfGHLCQvpCwULpQvfFtYWF3YX7iDy1HyfDlWTpAT5ZVyqrxR
zpEL5RK53Cm/lz/I/UmPsMePjxWPDY+Dj6OP24/ux8tHMAVCgVLwFAqNwqBw
KTxKB0VA6aKIKDKKgqKl6CkzlEWKkWKiWCgOiie+rqiurqmuuY5V11Y3XCer
U9dN1enqZuvMdY6647onuB1lx9oJdqK90s6x8+1Cu8Qutcvt0/Yl+4p9zW53
2u/tD/a/dn+SGCb+KMaIK8R0cYOYLxYPiofEUvGoWCneErvFl+JHsVf8ktQN
6/7Yjemu6G7o7hZ3D3YPdY92K7vd3Zfdj90vYBfEhXdRXDQXw8V2cV08V4dL
4BK5ZC6FS+tadJlcey6XBzAWNhYxljiWN4YeqxrrHBsZG1sf2w+Ki42Lg8al
xWXFkeLIcdVxXXEDcRNxhjhjnCXOFncGCAgIC4gISAzICMgLQAdUBXQGjAQs
w60oK9ZKsBKtlVamlWPlW4VWiVVqlVuV1mnrknXFuma12q1bVqfVH/j90/f2
799/fN8DRoGiIqOikFG4qJooahQ7qieqN0oUNRmlidJGnUddRD0DdgJ2wnYi
dhJ3MnbQO1U7nTsjO2M7yzvrO/CCzAJUQX5BAbaAUEAsoBY0FggL5AX2AmfB
fcFDgR/mg/swPqyP6KP7mD6Oj+8T+iQ+qU/pW/NZfXbflu/I5/XBEYhMBAqR
jyhAYBE1CCqiESFEyBFOxDniAnGPeED8QfiDWyGt+FZKK6O1ldfa0Spo7WtV
tC627rW6Wq8DvmR8+VL1ZeTL8pffkSWIksyS/JISaklPSX/JeclFyZ8SP6Al
oCWsJaIlsSWjJa8F3fKlpaqlpbNlpGWsZbllvWUn9DX+te6V/tr02vzKem17
1b3Ovm6/Hrwev3pfAfMB82HzEfOJ88nzOfN58+j5qvmW+c75sfn59fmd+f35
q/k3uAqlylcVqLAqgoqoqlRRVY0qjkqokqikKrlKtaJaU1lVdpVTda96UPlU
fuAJ6CTyJOoEeYI7qTlhn/Sc9J6ITiZPNCfak5Pzk4uTZ0B6QHpYenpGel46
Ov1LelV6S/pI+nL6TnhpbGlcKbQ0tTStNLu0lFw6UDpROldqKDWWWkptpWel
d8EJkISErAR8AimBkdCa0JEgSOhLWEzYS7j+Hz/fLT0=
"]}, {EdgeStyle -> {
Directive[
Hue[0.63, 0.7, 0.5],
Opacity[0.7]]}, VertexStyle -> {
Directive[
Hue[0.63, 0.26, 0.89],
EdgeForm[
Directive[
Hue[0.63, 0.7, 0.33],
Opacity[0.95]]]]}, VertexCoordinates -> CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"], {
{Hue[0.63, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxfk/Gg4DAODvEjmGcktsUo7lzLHSNCpCSZRJUqQYJUdzRJdSjgxLOWoS
uUWInNNY6M96P+/zy5PK72/kA/7777+FoP/++//vgt7Fvst6V/yO9K76Xd87
GyAAEAaIAMQDEgHpgAxAHgANqAK0ADoBI4AxwDxgGbAO2AG8BYQFRAQkBqQH
ZATkBaADvgRUBbQEdAaMBMwHLAfsAMHAKCASmAvEAWuANCATyAJygTygCCgD
KoCTQC1QBzQBzcAj4AnQA3wOjA78FFgWWBvICGQHtgd+D/wRuBu4F+gJvAm8
DYoNigvKCioOIgWRg6qDBoImgmygKFA0KAaEA5WBakH1IDaoB9QLGgdNgjSg
DdAmaBd0CDoBnYJuQLfBkOCE4Kzg4mB8MCm4Org1uCO4L3gx2Ba8F3wdkhyS
ElIYUh7yLWQhZDVkP+Qu5C2UHtoU2hzKCm0LHQ2dDd0OPQg9DvWGvoZFhMWH
JYalh+WE5YWhw6rCWsI6w8bC5sPWw3bC9sOuwt7ef3j/8/3v99vv/4VDw9PC
s8OLwkvDyeFd4epwffhM+Fy4IdwYvhpuCXeE34U/RSRG5EWgI6oiWiI6I0Yi
xiLmI9YjdiL2I94ioyJLInsieyP7IycjNZG/Ik8izyMvIv+AIWAoOBdcBMaD
KWAamAHmgnlgAbgLLAIPg2VgBVgN1oJ1YD14BmwAG8EmsBnsALsgCRAoBA8h
QSgQGoQBaYXwIB0QAaQL0gdRQBYhRogJYoHYIHsQF+Q6ChmFi6qJokaxo3qi
eqNEUZNRmiht1EnUedRF1HN0THRZdG10fTQ7uj36R/R4tCZ6I3ozejf6MPo0
2hN9E30bg4spi6mNqY9hx/TGjMdoYjZiNmN2Yw5jTmM8MTcxt7FxsdDYrNji
2NJYUiw5tjp2IHYi1hhribXFnsVB49LisuJK40hx5LjquK64gbiJOEOcMc4S
Z4s7i8+Jz4tHxxfF18U3xbPi2+KH49XxU/G6+Nn44/ir+Kf414SsBHwCKYGR
0JrQkSBI6EtYTNhLuE5MTsxJzEtEJ1YltiR2Jo4lzieuJ+4k7ideJb5Bs6Cl
UDyUBCVDKVABtAs6AdVDZ6AGqBFqgdqgjiRY0sckTFJFUkNSd5I4aTBpKGk0
SZnkTrpMekx6gWFgFTA6rAHGhDXBmmF8WDdMDBuESWGjMCVsDbYFc8MuYY8w
L8yXnJNcnvwteT55IXk1eT/5Kvkp+S0lNSUtJTulMKU85VvKXMpCymrK3Yef
H35/2P7w72PDx+6P4o+jH90fLz8+pqalZqcWppamTqTOpZ6l3sERcBS8AI6F
E+BEeCWcCm+Ec+BCuAQuhcvhKvgKfA1uhdvhTvg9/AHug/vTstMK00rTyGkT
aXNphrTVtLO0O0QmAoXIRxQgShBYRA2CimhECBFyhBNxjrhA3CMeEH8QfmQu
EoesQdKQbCQXyUP2IkVIGVKBnERqkFqkGXmEPEF6kM/pGel56ej0L+lV6S3p
I+nL6TsZ6IwvGVUZLRkjGcsZO5mozPzMgsySTGwmNbMxsz/TmXmeeZF5n/mQ
+SfTn1WcRcoiZ1Vn9WUtZhmzLFm2rOtP7Z86Pn3/9OPT3qdrVD6qAIVFEVBE
FBXViOKghCg5SoWyouwoJ+oe9YDyZxdml2ZPZM9lG7JXs8+y73LyctA5RTnl
OVM58zmrOfs5VzlPOW+5uNyaXFouM5eVy83l5YpyZbmKXG2uLteUa849yn3O
Q+dV5bXkdeaN5U3lzeft513lPeW95Rfkl+Rj8wn5xHxqfmO+MF+er8p35t/n
P+T/yfcXYAsIBcQCakFjgbBAXqAqsBc4C+4LHgr86Cp0C7oTPYIeQ8+jl9Hr
6B30W2F54bfCucKFwtXCu6K6ouEiWZG6aKpIV6QvmimaLTIUOYquip6KScXV
xX3FA8W2EmpJT0l/yXnJRcmfEv/nr58rPg9+Hvo8/Xnp88rnv59fMBUYOqYB
w8TwMd0YMWYQM4SRYpSYacwSZg2zhXFjLjFejA/zgiVgidgaLBXbiOVghVg5
VoVdw1qxdqwTe499wPqw/lJy6UDpROlcqaHUWGoptZWeld7hanA0HBvHxfFw
vTgRToZT4CZxGpwWZ8Yd4U5wHtzzl6ovLV9Gvix/+V1WW1ZfNl62UbZZtlt2
WHZadlN2iyfhKXganoFvxfPwHXgBvgvfh1fgF/FGvAlvwdvwe3gX/vpr5VfJ
16Gv01+Xvq58/fv1pfxb+Vz5Qvlq+X75Vfld+VtFQwW/ortCXDFYMVQhrVBW
TFdsVbgrLiseK14IREIlgUpoJHAIQoKEICeoCCsEK8FOcBLuCQ8EP7GSSCU2
EjlEIVFClBLlRBVxhbhGtBLtRCfxnvhA9BH9JDKpmtRHWiQZSRaSjXRdyakU
Vkoq5ZWqyunKpcqVSmulvfJvVUtVZ9VI1VjVfNVy1XrVDrma3EUeIE+Q9eQZ
soFsJFvINvJZdV/1QLWl2lZDremtmazR1hzVnNSc11zUPNfW17Jr22t/1I7X
amo3ajdrd2sPa09rb2pvKTQKg9JK4VJ4lA6KgNJFEVFkFAVFS9FTZiiLFCPF
RLFQHBQXxUNtpAqpcqqKOkl1Us+pF9R76gP1D9Vf11TXXMeqa6sbrpPVqeum
6nR1s3XmOkfdcd1T3SuNQWPTuDQerYMmoIloMpqCpqXpaSaameaguWieenZ9
b/14vaZ+o36zfrf+sP60/qb+ls6kN9Gb6Sx6G51PF9NH6Uq6jr5F36Yf0I/p
brqX7qO/NnQ3iBsGG4YaRhuUDe6Gy4bHhpdGYaO8UdXobLxvfGj0M9iMVgaP
0c7oYAgYIoaCscgwMfYYLoaHcc1sYjYzWUwOs43JZ0qZSqaZuca0MreYR0wv
09fU3MRqamsabtI1zTaZm7aatpsOmo6bvE2v3+a+LXxb/XbXzGpuax5t1jXP
Npubt5q3mw+aj5u9za+sNhaXNcySsdQsHWuWZWZtsQ5YR6xjlpf12tLZMtIy
1jLfstyy3rLD5rFFbAVbw9ayd9mH7BO2i+1h37Bv2c+tvNaOVkFrX6uidbF1
r9XVes3hc4QcCUfKkXOUHBVnibPCWeNYOXbOFsfJ8XH8bcNt6rapNl3bbJu5
7aDtuM3b9srlcQVcEXeYK+MquGqulqvjmrhmroN7xHVxPdxnXgdPwBPxZDwF
T8vT80w8M8/Bc/E8vOf2jvbv7T/a99pvOwQdfR2KjsWOvQ5Xh6fjmi/mS/iD
fClfyZ/mL/FX+Gt8K9/O3+K7+V6+r3Okc6xzvnO9c6dzv/NN0CUQCWQChUAv
mBEsCowCk8AicAj2BC6BRygRSoVyoUq4IlwTWoV2oVN4L3wQ+oT+Ln3XTJeh
y9hl6rJ02boc3eLuwe6h7tFuZbe7+7L7sfvl+4/vez29Pf09kz2anl89Jz3n
PRe9/b2TvZrew96T3vPei95nkUykEGlFJpFZdCJyiTyiZ/GgeEgsFY+KleIt
sVt8KX4Ue8UvfYt9tr5riVQil6gk05IlyYpkTWKV2CVOyV+Jr/9X/3n/Rf+f
gYkB28DZ4NCgcnB60D14Ofg4+DI0PbQ05B66HPo79CJVSlXSaemSdEW6JrVK
7dItqVvq+7H343ZYNqwenhrWDeuHZ4dNw+Zhx/Dx8NPI2MjyyPrIzuj26MGo
e/Ry9HHUO/pvbH5sfWxnbF+mkKllWplOppeZZGaZQ3Ykc8k8sudxzfiv8Y3x
zfHd8cPx0/Gb8dsJ44RlwjZxJlfJrXK73Cm/lz/I/QqtwqQwKxwKl8KjeFZO
K9eUVuWW0q28VHqVPtWKak1lVdlVTtW96kHlU/nVU2qdWq+eUc+qTWqz2qF+
mtRMnkyeT15MPms2NJuaXc2h5kRzqvFobjS3Wp3WpDVrj7QnWpfWo32e0k3p
p2anHFNXU0+6WZ1Z59Ad6Y51Xt2rfkZv0Bv1Jr1F79A/TS9Nr0xbp+3Tf6df
ZuZmDDPGGdOMZcY245g9mD2efZp9nTPMrc7dGYyGVYPFYDM4DGeGu/n1+Z35
/fmr+befv39u//y3sLqwv3C3aFvcW3QtXi+tLFmX7Et/f23+Ovx1arQYbUaH
8Wx5x2Q2OUwuk8d8ZD42P69YV+wrf1evVu9Wn9asa/a1rbWjNe+ab33HYrOc
We3WLavT6rP6f2///rexubG7cbhxunGzcbu5u3m4ebp5s3lrd9rv7Q/2v3af
3b91tOXe8m75tg+2j7cft73b/7ZfHU+7h7unuze7t3uuvev9q/23g+MD78Hr
4enhzeHtkffo+ch37D1+dd47H5z+k/OTi5Pn05vTW5fn/OL8z8Uf96X70e11
v1w+Xr5cPV29eW49zze39w/3/ge/1+d9fXr7H9QpLT0=
"]], 0.045176762611313204`]},
{Hue[0.63, 0.26, 0.89], EdgeForm[{Hue[0.63, 0.7, 0.33], Opacity[
0.95]}], SphereBox[1, 0.045176762611313204`], SphereBox[2, 0.045176762611313204`], SphereBox[3, 0.045176762611313204`], SphereBox[4, 0.045176762611313204`], SphereBox[5, 0.045176762611313204`], SphereBox[6, 0.045176762611313204`], SphereBox[7, 0.045176762611313204`], SphereBox[8, 0.045176762611313204`], SphereBox[9, 0.045176762611313204`], SphereBox[10, 0.045176762611313204`], SphereBox[11, 0.045176762611313204`], SphereBox[12, 0.045176762611313204`], SphereBox[13, 0.045176762611313204`], SphereBox[14, 0.045176762611313204`], SphereBox[15, 0.045176762611313204`], SphereBox[16, 0.045176762611313204`], SphereBox[17, 0.045176762611313204`], SphereBox[18, 0.045176762611313204`], SphereBox[19, 0.045176762611313204`], SphereBox[20, 0.045176762611313204`], SphereBox[21, 0.045176762611313204`], SphereBox[22, 0.045176762611313204`], SphereBox[23, 0.045176762611313204`], SphereBox[24, 0.045176762611313204`], SphereBox[25, 0.045176762611313204`], SphereBox[26, 0.045176762611313204`], SphereBox[27, 0.045176762611313204`], SphereBox[28, 0.045176762611313204`], SphereBox[29, 0.045176762611313204`], SphereBox[30, 0.045176762611313204`], SphereBox[31, 0.045176762611313204`], SphereBox[32, 0.045176762611313204`], SphereBox[33, 0.045176762611313204`], SphereBox[34, 0.045176762611313204`], SphereBox[35, 0.045176762611313204`], SphereBox[36, 0.045176762611313204`], SphereBox[37, 0.045176762611313204`], SphereBox[38, 0.045176762611313204`], SphereBox[39, 0.045176762611313204`], SphereBox[40, 0.045176762611313204`], SphereBox[41, 0.045176762611313204`], SphereBox[42, 0.045176762611313204`], SphereBox[43, 0.045176762611313204`], SphereBox[44, 0.045176762611313204`], SphereBox[45, 0.045176762611313204`], SphereBox[46, 0.045176762611313204`], SphereBox[47, 0.045176762611313204`], SphereBox[48, 0.045176762611313204`], SphereBox[49, 0.045176762611313204`], SphereBox[50, 0.045176762611313204`], SphereBox[51, 0.045176762611313204`], SphereBox[52, 0.045176762611313204`], SphereBox[53, 0.045176762611313204`], SphereBox[54, 0.045176762611313204`], SphereBox[55, 0.045176762611313204`], SphereBox[56, 0.045176762611313204`], SphereBox[57, 0.045176762611313204`], SphereBox[58, 0.045176762611313204`], SphereBox[59, 0.045176762611313204`], SphereBox[60, 0.045176762611313204`], SphereBox[61, 0.045176762611313204`], SphereBox[62, 0.045176762611313204`], SphereBox[63, 0.045176762611313204`], SphereBox[64, 0.045176762611313204`], SphereBox[65, 0.045176762611313204`], SphereBox[66, 0.045176762611313204`], SphereBox[67, 0.045176762611313204`], SphereBox[68, 0.045176762611313204`], SphereBox[69, 0.045176762611313204`], SphereBox[70, 0.045176762611313204`], SphereBox[71, 0.045176762611313204`], SphereBox[72, 0.045176762611313204`], SphereBox[73, 0.045176762611313204`], SphereBox[74, 0.045176762611313204`], SphereBox[75, 0.045176762611313204`], SphereBox[76, 0.045176762611313204`], SphereBox[77, 0.045176762611313204`], SphereBox[78, 0.045176762611313204`], SphereBox[79, 0.045176762611313204`], SphereBox[80, 0.045176762611313204`], SphereBox[81, 0.045176762611313204`], SphereBox[82, 0.045176762611313204`], SphereBox[83, 0.045176762611313204`], SphereBox[84, 0.045176762611313204`], SphereBox[85, 0.045176762611313204`], SphereBox[86, 0.045176762611313204`], SphereBox[87, 0.045176762611313204`], SphereBox[88, 0.045176762611313204`], SphereBox[89, 0.045176762611313204`], SphereBox[90, 0.045176762611313204`], SphereBox[91, 0.045176762611313204`], SphereBox[92, 0.045176762611313204`], SphereBox[93, 0.045176762611313204`], SphereBox[94, 0.045176762611313204`], SphereBox[95, 0.045176762611313204`], SphereBox[96, 0.045176762611313204`], SphereBox[97, 0.045176762611313204`], SphereBox[98, 0.045176762611313204`], SphereBox[99, 0.045176762611313204`], SphereBox[100, 0.045176762611313204`], SphereBox[101, 0.045176762611313204`], SphereBox[102, 0.045176762611313204`], SphereBox[103, 0.045176762611313204`], SphereBox[104, 0.045176762611313204`], SphereBox[105, 0.045176762611313204`], SphereBox[106, 0.045176762611313204`], SphereBox[107, 0.045176762611313204`], SphereBox[108, 0.045176762611313204`], SphereBox[109, 0.045176762611313204`], SphereBox[110, 0.045176762611313204`], SphereBox[111, 0.045176762611313204`], SphereBox[112, 0.045176762611313204`], SphereBox[113, 0.045176762611313204`], SphereBox[114, 0.045176762611313204`], SphereBox[115, 0.045176762611313204`], SphereBox[116, 0.045176762611313204`], SphereBox[117, 0.045176762611313204`], SphereBox[118, 0.045176762611313204`], SphereBox[119, 0.045176762611313204`], SphereBox[120, 0.045176762611313204`], SphereBox[121, 0.045176762611313204`], SphereBox[122, 0.045176762611313204`], SphereBox[123, 0.045176762611313204`], SphereBox[124, 0.045176762611313204`], SphereBox[125, 0.045176762611313204`], SphereBox[126, 0.045176762611313204`], SphereBox[127, 0.045176762611313204`], SphereBox[128, 0.045176762611313204`], SphereBox[129, 0.045176762611313204`], SphereBox[130, 0.045176762611313204`], SphereBox[131, 0.045176762611313204`], SphereBox[132, 0.045176762611313204`], SphereBox[133, 0.045176762611313204`], SphereBox[134, 0.045176762611313204`], SphereBox[135, 0.045176762611313204`], SphereBox[136, 0.045176762611313204`], SphereBox[137, 0.045176762611313204`], SphereBox[138, 0.045176762611313204`], SphereBox[139, 0.045176762611313204`], SphereBox[140, 0.045176762611313204`], SphereBox[141, 0.045176762611313204`], SphereBox[142, 0.045176762611313204`], SphereBox[143, 0.045176762611313204`], SphereBox[144, 0.045176762611313204`], SphereBox[145, 0.045176762611313204`], SphereBox[146, 0.045176762611313204`], SphereBox[147, 0.045176762611313204`], SphereBox[148, 0.045176762611313204`], SphereBox[149, 0.045176762611313204`], SphereBox[150, 0.045176762611313204`], SphereBox[151, 0.045176762611313204`], SphereBox[152, 0.045176762611313204`], SphereBox[153, 0.045176762611313204`], SphereBox[154, 0.045176762611313204`], SphereBox[155, 0.045176762611313204`], SphereBox[156, 0.045176762611313204`], SphereBox[157, 0.045176762611313204`], SphereBox[158, 0.045176762611313204`], SphereBox[159, 0.045176762611313204`], SphereBox[160, 0.045176762611313204`], SphereBox[161, 0.045176762611313204`], SphereBox[162, 0.045176762611313204`], SphereBox[163, 0.045176762611313204`], SphereBox[164, 0.045176762611313204`], SphereBox[165, 0.045176762611313204`], SphereBox[166, 0.045176762611313204`], SphereBox[167, 0.045176762611313204`], SphereBox[168, 0.045176762611313204`], SphereBox[169, 0.045176762611313204`], SphereBox[170, 0.045176762611313204`], SphereBox[171, 0.045176762611313204`], SphereBox[172, 0.045176762611313204`], SphereBox[173, 0.045176762611313204`], SphereBox[174, 0.045176762611313204`], SphereBox[175, 0.045176762611313204`], SphereBox[176, 0.045176762611313204`], SphereBox[177, 0.045176762611313204`], SphereBox[178, 0.045176762611313204`], SphereBox[179, 0.045176762611313204`], SphereBox[180, 0.045176762611313204`], SphereBox[181, 0.045176762611313204`], SphereBox[182, 0.045176762611313204`], SphereBox[183, 0.045176762611313204`], SphereBox[184, 0.045176762611313204`], SphereBox[185, 0.045176762611313204`], SphereBox[186, 0.045176762611313204`], SphereBox[187, 0.045176762611313204`], SphereBox[188, 0.045176762611313204`], SphereBox[189, 0.045176762611313204`], SphereBox[190, 0.045176762611313204`], SphereBox[191, 0.045176762611313204`], SphereBox[192, 0.045176762611313204`], SphereBox[193, 0.045176762611313204`], SphereBox[194, 0.045176762611313204`], SphereBox[195, 0.045176762611313204`], SphereBox[196, 0.045176762611313204`], SphereBox[197, 0.045176762611313204`], SphereBox[198, 0.045176762611313204`], SphereBox[199, 0.045176762611313204`], SphereBox[200, 0.045176762611313204`]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
ImageSize->{384.9535460577531, 375.},
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}},
ViewPoint->{0.944451038322406, -1.7391349078250222`, 2.744708000607019},
ViewVertical->{-0.2574628756358374, 0.1876871719619685, 0.9478852215064035}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/35a13d0f4aa999a3.png)
|
| In[24]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][saddleGraph, 2, \
{-0.11849417602213196`, -0.29735987618366094`, \
-0.07273251971244428`}, {0.530484850941491`, -0.9451892968127409`, \
-0.6112471689268776`}]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/1ddf47358380dc54.png)
|
| Out[24]= |
|
Show the geodesic tubes with radii up to 3 as a highlighted graph:
| In[25]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][saddleGraph, 2, \
{-0.11849417602213196`, -0.29735987618366094`, \
-0.07273251971244428`}, {0.530484850941491`, -0.9451892968127409`, \
-0.6112471689268776`}, 3, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/52b91451041e5a4b.png)
|
| Out[25]= |
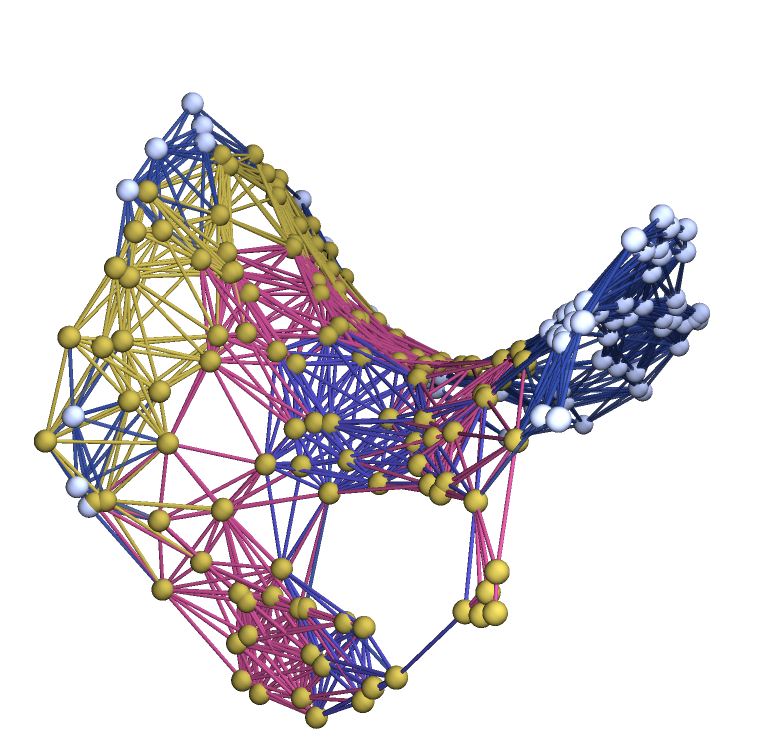
|
Compute the Wolfram–Ricci scalar curvature at vertex 150 in a 20-by-20 2-dimensional grid graph:
| In[26]:= |
|
| Out[26]= |

|
| In[27]:= |
|
| Out[27]= |
|
Compute the maximum and minimum scalar curvatures over geodesic balls with radii up to 8:
| In[28]:= |
|
| Out[28]= |
|
| In[29]:= |
|
| Out[29]= |
|
Return a list of all scalar curvatures over geodesic balls with radii up to 8:
| In[30]:= |
|
| Out[30]= |
|
Show the geodesic balls with radii up to 8 as a highlighted graph:
| In[31]:= |
|
| Out[31]= |
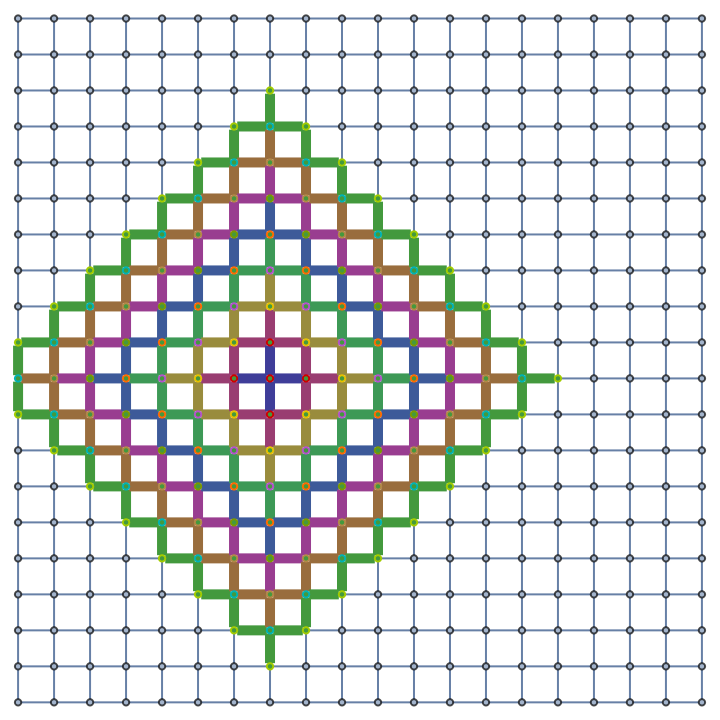
|
Return an association showing the Wolfram–Ricci scalar curvatures at each vertex:
| In[32]:= |
![Take[ResourceFunction["WolframRicciCurvatureTensor"][gridGraph, 2, All, All, "AllScalarCurvatures"], 50]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/74b51f342b7bdf88.png)
|
| Out[32]= |

|
Compute the maximum and minimum scalar curvatures across all vertices:
| In[33]:= |
|
| Out[33]= |
|
| In[34]:= |
|
| Out[34]= |
|
Compute the average scalar curvature across all vertices:
| In[35]:= |
|
| Out[35]= |
|
Compute the average volume of geodesic balls around vertex 250 in a 10-by-10-by-10 3-dimensional grid graph:
| In[36]:= |
|
| Out[36]= |

|
| In[37]:= |
|
| Out[37]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 3 and 9:
| In[38]:= |
|
| Out[38]= |
|
| In[39]:= |
|
| Out[39]= |
|
Return a list of all volumes of geodesic balls with radii between 3 and 9:
| In[40]:= |
|
| Out[40]= |
|
Show the geodesic balls with radii between 3 and 9 as a highlighted graph:
| In[41]:= |
|
| Out[41]= |
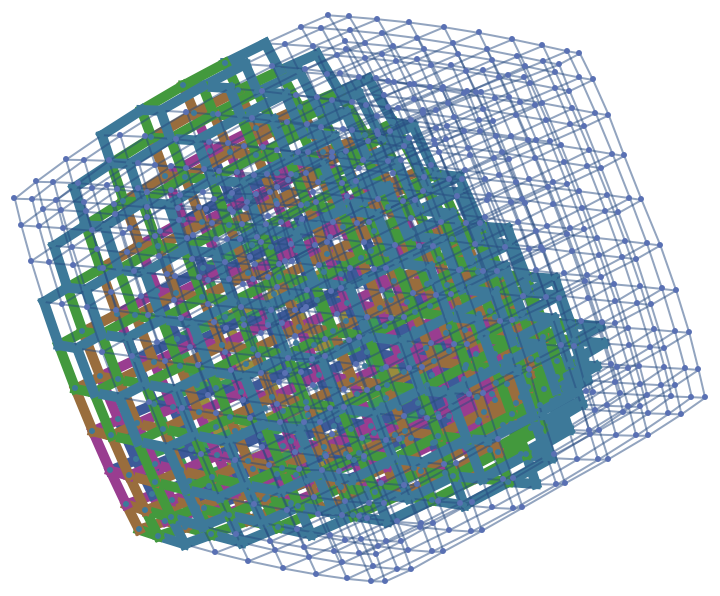
|
Return an association showing the geodesic ball volumes around each vertex:
| In[42]:= |
|
| Out[42]= |

|
Compute the maximum and minimum ball volumes across all vertices:
| In[43]:= |
|
| Out[43]= |
|
| In[44]:= |
|
| Out[44]= |
|
Compute the average ball volume across all vertices:
| In[45]:= |
|
| Out[45]= |
|
If given a graph, a number of dimensions and a vertex, WolframRicciCurvatureTensor returns an association showing the projections of the Wolfram–Ricci curvature tensor to each vertex in the graph, using the graph radius as the maximum geodesic tube radius:
| In[46]:= |
|
| Out[46]= |

|
| In[47]:= |
|
| Out[47]= |

|
Use geodesic tube radii between 3 and 5 instead:
| In[48]:= |
|
| Out[48]= |

|
If given a graph, a number of dimensions, a pair of vertices and a maximum radius, WolframRicciCurvatureTensor returns the projection of the Wolfram–Ricci curvature tensor between those vertices:
| In[49]:= |
|
| Out[49]= |
|
WolframRicciCurvatureTensor also supports directed graphs:
| In[50]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAYA7mmYAq3T8IxMSUWUrvP5TMvnnQ
Lu4/LPamrnjK7j9QXnoCq1nTPzg1VJeN3t0/gKRhpA6Prz+MxpBJZq7YP6jd
7/Z4gts/NlJMenjr6D8g1/Po3OCoP0D+PCTDGuQ/FFsxworK0T+wlLzYgBi3
P4zmzJ7/DOw/kJ1Jc3Huuz9gxKG6LALRP3RBVtc/Ze0/CEUth86/xT8AmE9j
+X25P9iRiKm5F94/0CMkyq3O2T90KAweOhfvP1wVFVHLJ9Q/6BGcj40ZwD94
UfWCtWzRP0JdY8FIYuM/GsVMrRV/5T9os9Hh/gbPP8CLTPixed8/mOCTVqED
4j/EeX89A5PhP6gzJK2w0t4//qPE3b2d5D+4SkeOJ7naP2bh/wlxi+Y/vJjb
NDrD7j/UanOC/evsP+CtTggX2+s/aPfhhZE25D/MNKin
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 3, 5, 6, 7, 10, 11, 11, 11, 14, 14, 16, 17, 19, 20,
21, 23, 25, 28, 30, 31}, {{5}, {12}, {14}, {16}, {19}, {
13}, {13}, {4}, {17}, {18}, {4}, {6}, {17}, {18}, {7}, {
10}, {8}, {7}, {10}, {16}, {13}, {8}, {11}, {13}, {16}, {
3}, {15}, {16}, {11}, {20}, {12}}}, Pattern}], Null}, {
EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx1lg9YTOkex2em+adppj9T4ZLIpa2UFpVcvK9N6Fnh6Q+yl6ehWhtLLN0N
Udom8l9ZlM2VNnFx++OixHtWi8rfohRl8y+SmD/NaKZpus055z3z7Dz290zP
22fO+877nt/3+z3PGbV8bVgsh8VivR74M41/LkdI/0NQgx3NCkB/T7MQfp7t
/uJ7BbLYiLDgv1iPC69nzkF8/lwMsz5/TsvftTwnc15gsZ74PDPrabazYKEF
W+7P9Bf9eT7zOxbz8bks+8T0F0rflH1xZX4VOrwx61LKHSkcfHUhjN3bgGxb
ivYK90hhhE9v6u3m52jlRJh+eIYUjvju2Npy0Tt0fHNUrvc7B5iYkTFp63kl
unih+0Gt3AG27PMIqG3XovPP7MeuHewAfw+9gIjzBiTXFef87Zg9/LlN+sY3
jU1M49X73HW0hyLNjJJGLZd4xN74Qp5qBzn5nuGqozxiiS1HGiKzg9YFZzNa
PfjElcmt70dOsYNuvbfmHSnkE7pkfoLExg6GnNpS5GYnIEZd6508+rwtTC2q
zd4SJyCEl+WvIvxtYY2xRFp4WkAUdpx7UVIsgSPPTBhzvFlAGMLWTZziIoE7
zsyt+VYrIKy7HzR2bRYz/Z9Ilgj2kyUg6tyT692TrZnr64ffWjf81iDIpllq
b6pBzPVi3jcDH7OeC/QF8/UFAoY/fjAVn+G9LycPfMzs07Tdu2k7j+FJ5Hms
4MFIJ9DcIyCWPfQcMyKFA+ctjDTEvBQQubXJlZp6NhzPIQJOIgGhGDJOV+7F
hn5RkcqsPQJi8TW/p/GZLLjiGyePgFABcXaj3w27Z/3gspD1x24jn6gffnHE
mDIjmCRzkh46wSfc1nddd8juAw0xkTfm+/OJ3I1PS5pTDCBPSmgqK3nEdPeU
zqSkXsC/H3oipplLSPJyv6op1YEtAfd5znwuoVuTJxpn0wP65s4cXfeVFdF7
dMes/HQtyLQ9pzu0j0NIXZeovVw1wG3boJ0x79lEsNHBoaZJDapzo+qmRrGJ
/QFl+UmlKpAU+0v9iEYWoaqd8uu0s0oQ0PJot/UKFvH95dNDnW6a83v62/cv
NPeljP8XF9hMbc0xs83FaNHFaDNXHXu7IGWUmbeSCxwYBh1Z0zuyzMydf6k9
I9jMd3ZKeENU9gznHDWVmd+Zlk83cyApMJNDVuYOU5mZlNvbzJRfbBlWkH6R
MEz5xcyUX8QM371jKhuGyfYMM7NedmCCYoOI4Z9M2zdZM0zdr5k33/RZ1l85
iGHq/sxMTq81P3/O+rpPcYwWwlN5Jbseg34Ufr/pRudxW7jctO0qIyqZM/TH
Cj9bSJ27Dw1Z/Zvz6t8k0OaH/CC23IDSA+tOsIIkkDpnLzIUmxaIIdmW+Xq0
td4USDE0qezqrEP8vDV3bXfZwC9N21Z/QkekLta+r0Qwjiwtwnk+SS7vRjjP
ZBv3qhHO82g3U6kQzrNMZDKOAuE8U774gHCeK6+YqhPhPFM6v0U4z6TtRO0I
55k6x0tEynOHC8n2rG1DcaQ+XHjPdld26qmniLpvKziY7EsjovThQFPXwLh6
ROnDgUWksLfRJlIfNsw2ydJRhSh92LCto3GgdeWI0ocFjZ4m5xYhSh8W/A+t
E9YH64j16aB1xvpgH2B9sE+wPmm0j7A+2GdYn5W0D7E+2KdYn+njwgamiiHW
59HERKX+jRhiffbRvsf6rPpHTssimQRifeJpxvrgnGB9Gunfw/pAej+sDz4P
1gfnBuuD7wfrg3OD9cH9wPrgfmF9cG6wPrjfWB+cG6wPzhOdI+Z5R+eIYTpH
DNM5YpjOkZmpHJnnUzlimM4Rw3SOQHXHbpfNg9cjF79jkq08Dc0HUfU9p0xV
hRqwM6anxi8pGHhfeNhUJVfR10vRp+WP9MqVShDiPW5Z8cxKtHnpUMUWmYKe
/zt6HjxzXU3bB6C/AdK7y26jC3GtRWFeXfT6erTKxSg/lN8Jni+Kq7v0uhEJ
4wtFB2e9A1Gjrf7rrH6JwtZsLdrAbwcApO7SVHciWTSYkj7sBXiAnMHUTUoU
k1KfmiFqBdNUaVX3K7qRfFjPj9GZjeCtvzDcr/ATGn/wY9Shsgegfs/JrtVT
9aiiel3IXMkt0KONzEpMNqDAOQtiv3asBMvWu84M+86IvJ4Irz2NPw1wfiLI
/AgYPUvJ/AiY/FA55jN+kJP54TN+6SPzw7PID4/xm5DMD5fJz1EyP1aMX/H7
QWfFgrGKVWI4JmfO6j9SOFC+JmFdUKsYlr/ubtI3sOG/33idvzlSAlVOk5PS
J7DhxLFpLUn+EnjP0yF0288sGOSZaPjnCAmc9/e0iLdsFqxXcyUJTWL4guvs
mtphBE+2j7cvixHDhMxwg+2zPiB7rOGNrbKBs5uvweTnBrBCueh9tVoEqbEX
VLC31a2WWkNq1IM5Gdxgj4VCSI09QLT97SzjFT6kRi3gqDwfd87kQWrUAN/H
tzVKhRWkRjXI/vJ2vh3BgdSoAt5sj2ezS9mQGpXAEPz61OFbLEiNCnBw9sL2
d4H9qGa01w+aYwIo8bux5Hq4Ee3IWe793EMA11fPXSoP7UOBMYU+VYV8WMnu
6vJ3N6BnKdrEXCkfdrX9avOoTY8SFWH8+AQeFMT9q3zpJh3ill1p8bnKhcID
su6H6k/op2pffYfOCqpkMVf9Q7VI51u6LHesFbzetM1RLu9GsvfAOiiIAyP8
IzdGZ6nRhGAH9yzEhkemNTQ3VKrQx1k787R+bLj/Q/+Mdo4KHVEWJHxfyIKB
IQ3nDsQqkWdw7C+f7FjwUGikS9MrBVqQlh3i2WkEBb3b9penKJDbvVPi3UV9
IDY8UuAfqEDV8dwMxyUG8CSiITVUokCzo878r6of512BqPcVHcOkfQN6GFZX
ucW2dWgBm2aB6fFarGGuC0g/djOs2b200pikZpi0b7KKYXJ6tpLhxbJ5G74g
FOD/jiRXzA==
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 5}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 12}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 14}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{2, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 16}], 0.043048128342245986`], ArrowBox[{2, 19}, 0.043048128342245986`], ArrowBox[{3, 13}, 0.043048128342245986`], ArrowBox[{4, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{5, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 4}], 0.043048128342245986`], ArrowBox[{5, 17}, 0.043048128342245986`], ArrowBox[{5, 18}, 0.043048128342245986`], ArrowBox[{6, 4}, 0.043048128342245986`], ArrowBox[{9, 6}, 0.043048128342245986`], ArrowBox[{9, 17}, 0.043048128342245986`], ArrowBox[{9, 18}, 0.043048128342245986`], ArrowBox[{11, 7}, 0.043048128342245986`], ArrowBox[{11, 10}, 0.043048128342245986`], ArrowBox[{12, 8}, 0.043048128342245986`], ArrowBox[{13, 7}, 0.043048128342245986`], ArrowBox[{13, 10}, 0.043048128342245986`], ArrowBox[{14, 16}, 0.043048128342245986`], ArrowBox[{15, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{16, 152, 153, 154, 155, 156, 157,
158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 8}], 0.043048128342245986`], ArrowBox[{16, 11}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{17, 178, 179, 180, 181, 182, 183,
184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 13}], 0.043048128342245986`], ArrowBox[{17, 16}, 0.043048128342245986`], ArrowBox[{18, 3}, 0.043048128342245986`], ArrowBox[{18, 15}, 0.043048128342245986`], ArrowBox[{18, 16}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{19, 204, 205, 206, 207, 208, 209,
210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 11}], 0.043048128342245986`], ArrowBox[{19, 20}, 0.043048128342245986`], ArrowBox[{20, 12}, 0.043048128342245986`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.043048128342245986], DiskBox[2, 0.043048128342245986], DiskBox[3, 0.043048128342245986], DiskBox[4, 0.043048128342245986], DiskBox[5, 0.043048128342245986], DiskBox[6, 0.043048128342245986], DiskBox[7, 0.043048128342245986], DiskBox[8, 0.043048128342245986], DiskBox[9, 0.043048128342245986], DiskBox[10, 0.043048128342245986], DiskBox[11, 0.043048128342245986], DiskBox[12, 0.043048128342245986], DiskBox[13, 0.043048128342245986], DiskBox[14, 0.043048128342245986], DiskBox[15, 0.043048128342245986], DiskBox[16, 0.043048128342245986], DiskBox[17, 0.043048128342245986], DiskBox[18, 0.043048128342245986], DiskBox[19, 0.043048128342245986], DiskBox[20, 0.043048128342245986]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{237.3828125, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/6e07eeae3cda102f.png)
|
| In[51]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "Curvature"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/1dfed7905b5cba0c.png)
|
| Out[51]= |
|
In the directed case, projections of the Wolfram–Ricci curvature tensor are computed using volumes of geodesic diamonds, as opposed to geodesic tubes:
| In[52]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/72ca151cf8326764.png)
|
| Out[52]= |
|
However, WolframRicciCurvatureTensor can be made to treat directed graphs as though they were undirected (and hence revert to using geodesic tubes) with the option "UndirectedGraph":
| In[53]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "Curvature", "UndirectedGraph" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/21562100f27235d5.png)
|
| Out[53]= |
|
| In[54]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "HighlightedGraph", "UndirectedGraph" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/512dac9a3d96588c.png)
|
| Out[54]= |
|
WolframRicciCurvatureTensor also supports curvature computations in graphs with non-integer dimensionality, such as this Sierpinski sieve graph:
| In[55]:= |
|
| Out[55]= |
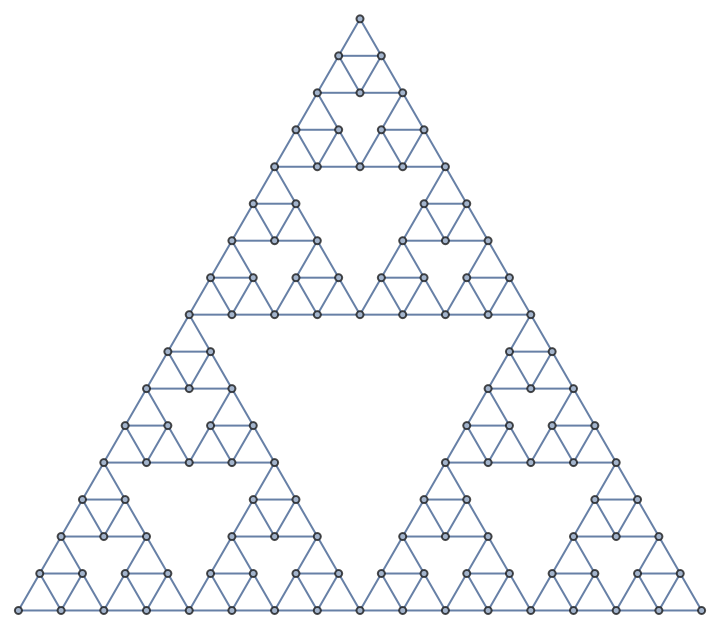
|
| In[56]:= |
|
| Out[56]= |
|
| In[57]:= |
|
| Out[57]= |
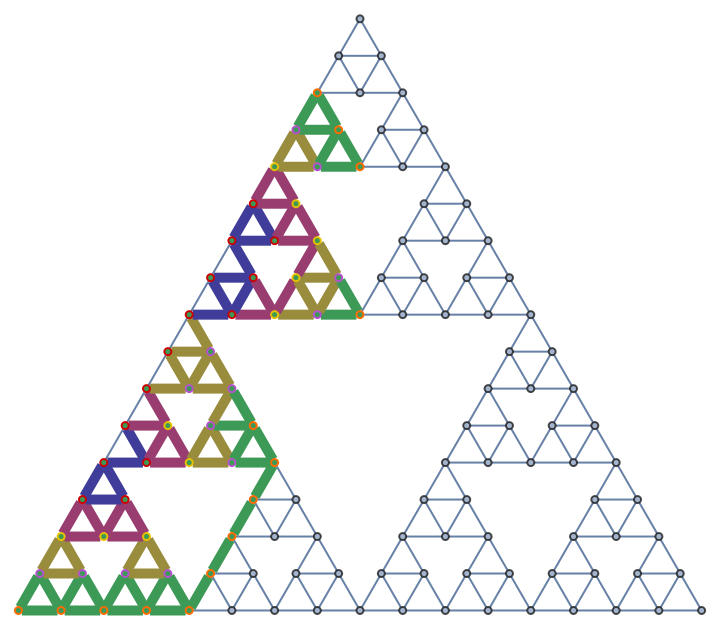
|
Compute the average projection of the Wolfram–Ricci curvature tensor over geodesic tubes between vertices 145 and 355 with radii between 2 and 6 in a 20-by-20 2-dimensional grid graph with the option value "CurvatureMethod"→Mean (default):
| In[58]:= |
|
| Out[58]= |

|
| In[59]:= |
|
| Out[59]= |
|
Return a list of curvatures over geodesic tubes with radii between 2 and 6 instead:
| In[60]:= |
|
| Out[60]= |
|
Compute the maximum and minimum curvatures over geodesic tubes with radii between 2 and 6 with the option values "CurvatureMethod"→Max and "CurvatureMethod"→Min, respectively:
| In[61]:= |
|
| Out[61]= |
|
| In[62]:= |
|
| Out[62]= |
|
By default, directed graphs are not transitively-reduced:
| In[63]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/03fcc6af-415c-4605-b77a-482fd8c95b3f"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/46c840d9d75054bb.png)
|
Compute (and visualize) the Wolfram–Ricci curvature tensor, assuming that the graph is not transitively-reduced:
| In[64]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "Curvature"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/72826b3cb5a52a2f.png)
|
| Out[64]= |
|
| In[65]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/3840fad3417affa4.png)
|
| Out[65]= |

|
WolframRicciCurvatureTensor can be made to treat unreduced directed graphs as though they were transitively-reduced with the option "TransitivelyReduce":
| In[66]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "Curvature", "TransitivelyReduce" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/4cd5ec5263dd8783.png)
|
| Out[66]= |
|
| In[67]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.4298384105199724`, 0.7787439716945019`}, {0.16991597748214127`, 0.09957846331198539`}, "HighlightedGraph", "TransitivelyReduce" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/0088c49bf581da0f.png)
|
| Out[67]= |
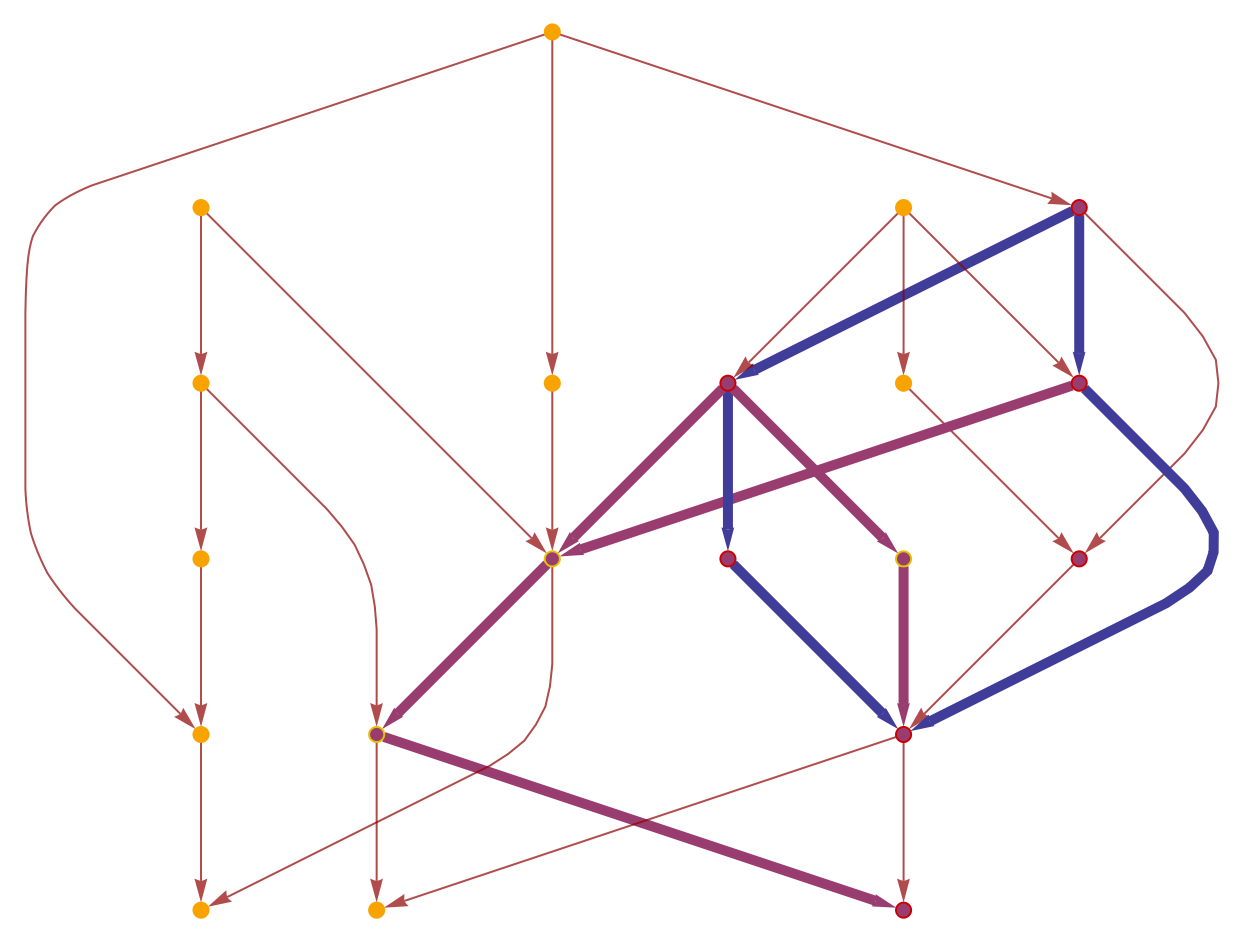
|
By default, directed graphs are treated as directed (and so curvature computations use the volumes of geodesic diamonds, as opposed to geodesic tubes):
| In[68]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAiBDgQC0N7D8Miwlf7rPgP2DD6g69
ErY/vFne0Lkv2D8AYqEgHNmHP0y+xxYqrO0/sBJhl3Rm4T9kbie+Xq3eP6hf
tX6aZ88/ki5iaxFR6D/KvOcIEIXvPyB5b3EiyMs/gEqJn4lg3T8W9qyLs0/s
P7qg/i7vruI/SMlbtu/k0D9I3gFvCW3tP1AaT8UdINs/TnYI2uGX7z/A7Age
bdDiP9B5FJWzMrU/DqNXMXBJ6T+sgi4Z70bmP85zrMZJD+g/cMA/h/uy2T/K
qgmYaj/kP1ycpAlxYeo/MJn6j48Euz9cbg+fJinePwzPqiEI19M/Siz/TIYE
6T/4ia6W8rHLP0BF9wTPFcs/riH/Ot0j7D/kWXJEIx/aP6SzChO3t+U/Pmkf
1Khk6z+AomBv3AKAP+Ys8tyO2+Q/SIuN6pq61D85Ap6m
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 1, 1, 3, 7, 12, 13, 16, 16, 18, 19, 23, 25, 26, 27,
27, 28, 30, 31, 31, 32}, {{9}, {11}, {14}, {8}, {15}, {
16}, {20}, {2}, {8}, {15}, {16}, {20}, {19}, {2}, {9}, {
18}, {6}, {16}, {9}, {2}, {8}, {15}, {19}, {1}, {4}, {
4}, {19}, {14}, {5}, {18}, {13}, {14}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxdmAs0lFsbx2cMc3GZGc2YmZKD41upSUihInvnlm50SEUlHF1IQn2OkCLX
cupDKEpRSaWSOiVHZpcuKIlKnE5FEXIb19zna+Y17yyeNWs96zf79rz73fv/
PDPanvscd8gRCAQVIoEg9lONCTFPRZNfTPJsNLWdMMnUSWZOY9wmWQgwz5tk
9rT5pSYdLxRMXU/aX9oujY89LZ7p8UnXlcaHxyOYtj6aGp+Up8+P27T5pPtD
ncbTn08aj9RL58fjnMb4fsJp8cCp/XnT1pMyPg+a2l+6H+xpzIQiiakjp6q6
p+3nGfjz3LabGVxkLGOe7yOO7yM6ztFLq7MIVjIeyxcPUME5vEb3UI2ujMmZ
fpWM48o4n2ZpKBo2KeG8SGJKeDzV4uGHFPH2wNnPA2Y/p+HMUhWbjPMVtvz8
yN7H+pFLDiOXKDh3d4mNjPOJr0t+fmSsXxe5oC5SAefFknhIsH9+5RnFUXWU
/DhdZ1W0HKy9tXgXv0Md+ccuv5fVQoQXjpvs3v5GHVVFqLebuxKhs6Dm7NV8
dXT99uLHsz4S4MBqmgItSh1RufFmZv4EeET/nwuH1qmjptu8TZksAuz3tvGn
qKijMPnn8+JOiMCG8dX7cx7PQkbMN22bOSKQ2fr9qqvfLNQc49x1s2QCVJGX
nHF15aLLS5JD7OzGQC6RU7Uqjo02EIMDs8gjYH591Jq5Q6pI2ECqfTD8A1yZ
RdPocGKgoPcmlxO1B8Eac77hTjMl9L2J2TA3vB9A7t7XJTkUtJaWFHOY0Qei
rlePD6TIo7PWRadT3vWAWcObCpVocqguNZ6z57X0fBEIVzJvH38PRDh7JhoJ
D+yZwBnbz3GclfdnWxFjxnAe8RAPGJWx+HU5jMj6m39M1+QM47xQdxnbvewH
zjslNgjK2hI0QrmBAg3js/RwhYFJThKUvVI71lvUB4ixFhE+rpcEuxe9qSuN
6Z1sLxD88Hw70rO7B6xaoOeWb10sCN02UxjmIZzs/0TQaGMdUN7QBUaeguj+
Oy8Ed3d+zHWc3zk5vkawR2MiJiW7HTRu2ll9v7lWQPXJUUqy/Q5cdEi3OH1f
BY5+4bkHyN8AABHHB8raBR7uYFm0+hfwWsAB5iE9Aq8jNRGxSh/B8t6jpVVF
/YIY9aFg92O1oNWE6mSc80NgkNTtknLnNaj582Knr/mIoKgsYNVa+nMwNOic
HHRoTLDUbv2ONexi4Baoae3oPSGY/w+15IPPVVxvru7q+DJQxYVSdrkk3lEu
JE6y8j13pXvusvbSs63rj2jL+PBm8QAOzqAt2aItWcbyDve/xdrIuDKersDr
VcM5/YzYZCwZbiHjpZILyMbjiY8Tm0wf68XHZ4GM54rloIaFc/AfYpOxWB0C
ZsuYK9GrGdPiUcX5uyQeGWPxMPF4jknikemz5DgvkDGmLwychRJ9oeOM6YuM
sfuggrNU73IKYCuq6wZ9cWf6X0cpwrMVclmk37vB0IUlI6iZBj+ttOWXZXaB
FaFMa9JGGvTlK0XREzpBBVe7Ju0dFdoF/nazlt8BTgf5XAr3osJAzZlXtUK/
g9y0jqL7clT4faHngY6wVjAackXNKp8C86/qMZcZfgNJWhl3tfZS4KOY4DBa
ylfgG/c8bf1SCnxt+KajzyMOvFw8GsYjk2GqN8Fd3qxRsGtY9MChQx7Osf8t
ft0FoWB57Tv7wXYSvHF55n8y3/8QrH4RZqasQIKeZi6EA1YTglN1/YcTTeXg
RQr1ZEsPEfEmls+OOUqE15nnSzZtlUfvzDYzv7cSYEVhzwlFDzJ6lWi19eEu
AvQtvDpT7ZkQNCWmPAh5xYW9FcsuL8/rAdbrbqcKT3Hh/0zvZB8s6AUaRk5p
Hk5caDMxY0Z5XR/YB0P/rqRxIUvTtW++5gAwD55HMi7kwJEzcbbZ0YMgsn6b
X5obBw75ZSrpKQ8BKy/eeP+YGmRkZliWFwyDQzyXW+uS1aCF7pH2gwdHwcJB
zegsbTWYV37t2HnfMXDm1/jk8s9suOsxfw7fahwEX7R2GE1nw0BVQsnM8XFQ
GexYaOLEhmX3+I5+6RMgNbvgVSiVDX0Lrn3RVReBt1o7kiqKWHCb/JF9todF
IK7Pm6Tjw4IZedeGyp+JQMGsR9rRHBbUvc4PL+gRAcdUn06hQHp+CVB6fjn7
v0S1dorAKpUrR7evUIWuL+NZ2fd/jt8fnV3cxYQVSoPX9baJwIeXiwfzs5jQ
a6GufdynCVDC+yvc3JUJ9ZZrjNw1mwDbN5HNt/OYUMug7lbBgXFwUPW3rUaF
DLiCsnlfRPwYyHMxvfZ2NQOeeHp2iXbIKNgaK/C43EqHmM6NgMj0tshLiXSI
6dwgSMnQ5J+LUIGYzvUCXt1J+8YYZYjpXCegr18m9M9SgpjOfQOBJE3G2mpF
iOlcA7DtXX49kKMIMZ17DxJmpz1p8qdBTOdeAstI/pbsBirEdO4B8NYZ8ru+
gwpn+fnYRi9ko3Kd+fsHzlJgcYG9N2MPG8Wley5onEeBzZV5uzPz2GipV45+
aQ4ZJgqirI0G2ejTkcGgDBYZPo2tHatYqYaChI5kH38FGD4nO3F3lhqSv/P3
v/oP5WFJRoucEomDosoMR9qGSTCqJWd9gS8HDRsWuGXMIcEqWkOI2ycO8ugA
ilZWctBH8r65yMhmhm6ygAjT84/FV6znom7b+MxBY+Lk++ei0z2X/PfmEGDB
jWOnMnK4iG+z49wPJmHyPHDR+qOnVvHbJwCP2JBR/ZmLfn11RSUhdxxg54OL
ynzkY9muY6BCcjy5aKXLtb9KRdL8yUPS/OjEoWrwRrmoRXVRWxZtAGxw0Trg
3vEznhUB/REv+sBYmZ1C/RsuOjyoFUfO6wX2OyJeR9zmomQDy0sG13/mR/2K
d67RXKTf+dZuvEwIunR01LwcuMjBoP6/+xSEwMI24cQ5Bhd1tJ/bqPyoC5ik
KFhSnnGQXaRvTeTdTlDHPGmQFchB+dq/bLds7gBp3oPDhspsJJEZXit41Sva
f75OFWU0i1osbn8F3Zs3mdXfYqCPt28GFWz/DPgL+joN2cpog+u3Dx5z64CD
5xuRzScqOvckR3S8uBq4Df3w59HJKKjxc6nHkjKwodt9Re5FEsoNoShZajwE
JivpAQOZROS5v4m5qfsqwOpLCsLyozRfUJEk3aWzJvWfirD8KGvH8qOMwyUD
ZuCMJTgZY/lRxi8l+VEVZ+l9TnJWA/VDFHTLO2UGA6pC+43OY15fKci+2eJT
SBsTGsgh04sCCjqonDr2bwoTGrs49yT/SUF6n9P3Gtsw4e9b1OaZrqOg2qJ0
T2o3AxZSCZ8TJsjIh77lZJILAy72UGOlZJER80GQB62CDt95OT91MPmpt0Wd
db6QDjNZaKC4WAGdl3gVSK5al+VVL48wrwzDTKsUOGR5hHllOL7WWqfakoQm
JF4JHmPcGE45KYcwrwh/PUyL9+ogIh2Jp8GyDJdqcxciwjwNHtxxruaXWgLC
PBWa/vs2QfF3AsI8FVbbCj9ufEFAa7qO2vErufCovPM960dE1FDiU3PzJBfy
lurHlzfKob8D7p77cyUXJjSFbmzWk0efyB7XnvVz4BeyxS+nsxWQXbj/kEsa
B/IuHGhotKSgkfdfYlcacKBhvua5xyo01M8q3HyyWA3yTcGGZSQlZGIk9FkI
1KC88RuFVToqSGB0vGTB/Z967ml/lvlQBTmaazncOM6GWaS8+8iajvhOTddS
XNkwiduxyaWIjmz+eF/9TYcNUzPph/7RYKDs3OHSCy0sWHCapWu9j4EsW1ZH
lF5mwSaFUefUmww0Z9ELmoMbC+p9e0Kr/sBA9gkh26xUWTBhaYBl/yADPejd
HHahRHp+mGhq/cJEU+sXJppavzDR1PqFiabWL0w0tX5hoqn1CxNNrV+YaGr9
wkSVL8WmjLPkOqnLGKvvlfB4osTL1yni7dj9kHHoM303UTENZ+z5ZCzpXiH7
/yHPUPyDgAr/D/YhGQA=
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 9}, 0.05783410138248847], ArrowBox[{3, 11}, 0.05783410138248847], ArrowBox[BezierCurveBox[{3, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 14}], 0.05783410138248847], ArrowBox[{4, 8}, 0.05783410138248847], ArrowBox[{4, 15}, 0.05783410138248847], ArrowBox[{4, 16}, 0.05783410138248847], ArrowBox[{4, 20}, 0.05783410138248847], ArrowBox[{5, 2}, 0.05783410138248847], ArrowBox[{5, 8}, 0.05783410138248847], ArrowBox[{5, 15}, 0.05783410138248847], ArrowBox[{5, 16}, 0.05783410138248847], ArrowBox[{5, 20}, 0.05783410138248847], ArrowBox[BezierCurveBox[{6, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 19}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 2}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 9}], 0.05783410138248847], ArrowBox[{7, 18}, 0.05783410138248847], ArrowBox[{9, 6}, 0.05783410138248847], ArrowBox[{9, 16}, 0.05783410138248847], ArrowBox[{10, 9}, 0.05783410138248847], ArrowBox[{11, 2}, 0.05783410138248847], ArrowBox[{11, 8}, 0.05783410138248847], ArrowBox[{11, 15}, 0.05783410138248847], ArrowBox[BezierCurveBox[{11, 174, 175, 176, 177, 178, 179,
180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 19}], 0.05783410138248847], ArrowBox[{12, 1}, 0.05783410138248847], ArrowBox[BezierCurveBox[{12, 209, 210, 211, 212, 213, 214,
215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 4}], 0.05783410138248847], ArrowBox[{13, 4}, 0.05783410138248847], ArrowBox[{14, 19}, 0.05783410138248847], ArrowBox[{16, 14}, 0.05783410138248847], ArrowBox[BezierCurveBox[{17, 235, 236, 237, 238, 239, 240,
241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 5}], 0.05783410138248847], ArrowBox[{17, 18}, 0.05783410138248847], ArrowBox[{18, 13}, 0.05783410138248847], ArrowBox[{20, 14}, 0.05783410138248847]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.05783410138248847], DiskBox[2, 0.05783410138248847], DiskBox[3, 0.05783410138248847], DiskBox[4, 0.05783410138248847], DiskBox[5, 0.05783410138248847], DiskBox[6, 0.05783410138248847], DiskBox[7, 0.05783410138248847], DiskBox[8, 0.05783410138248847], DiskBox[9, 0.05783410138248847], DiskBox[10, 0.05783410138248847], DiskBox[11, 0.05783410138248847], DiskBox[12, 0.05783410138248847], DiskBox[13, 0.05783410138248847], DiskBox[14, 0.05783410138248847], DiskBox[15, 0.05783410138248847], DiskBox[16, 0.05783410138248847], DiskBox[17, 0.05783410138248847], DiskBox[18, 0.05783410138248847], DiskBox[19, 0.05783410138248847], DiskBox[20, 0.05783410138248847]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{182.63671875, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/576bc86c1f3a572b.png)
|
| In[69]:= |
|
| Out[69]= |
|
| In[70]:= |
|
| Out[70]= |
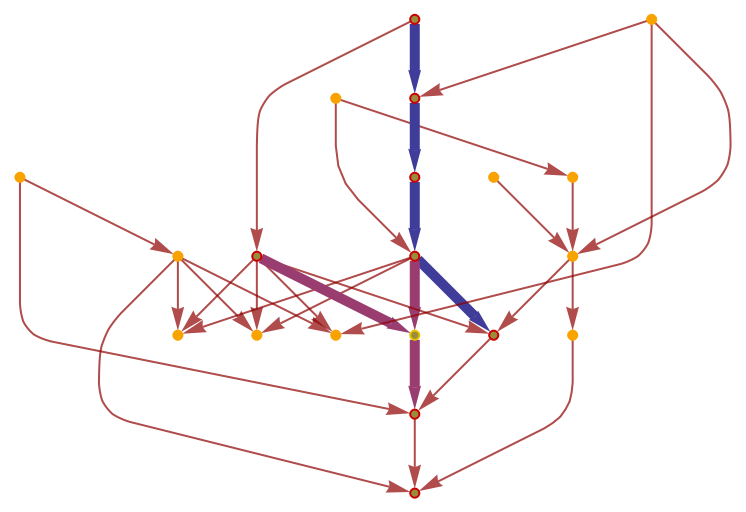
|
WolframRicciCurvatureTensor can be made to treat directed graphs as though they were undirected with the option "UndirectedGraph":
| In[71]:= |
|
| Out[71]= |
|
| In[72]:= |
![ResourceFunction[
"WolframRicciCurvatureTensor"][directedGraph, 2, \
{0.2116030477759896`, 0.879377951839208`}, {0.8560375350018956`, 0.00781795706650823`}, "HighlightedGraph", "UndirectedGraph" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/68aca2517fb75811.png)
|
| Out[72]= |
|
Return an association showing the geodesic tube volumes between vertex 145 and each vertex, with radii up to 3, in a 20-by-20 2-dimensional grid graph (default):
| In[73]:= |
|
| Out[73]= |

|
| In[74]:= |
![Take[ResourceFunction["WolframRicciCurvatureTensor"][gridGraph, 2, 145, All, 3, "AllTubeProjectionVolumes"], 50]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/7e6b0a2601f8073a.png)
|
| Out[74]= |

|
Compute the average tube volume between vertex 145 and all vertices with the option value "VertexMethod"→Mean:
| In[75]:= |
|
| Out[75]= |
|
Compute the maximum and minimum tube volumes between vertex 145 and all vertices with the option values "VertexMethod"→Max and "VertexMethod"→Min, respectively:
| In[76]:= |
|
| Out[76]= |
|
| In[77]:= |
|
| Out[77]= |
|
Return an association showing the projections of the Wolfram–Ricci curvature tensor between vertex 145 and each vertex, with tube radii up to 3, in a 20-by-20 2-dimensional grid graph:
| In[78]:= |
|
| Out[78]= |

|
| In[79]:= |
![Take[ResourceFunction["WolframRicciCurvatureTensor"][gridGraph, 2, 145, All, 3, "AllCurvatureProjections"], 50]](https://www.wolframcloud.com/obj/resourcesystem/images/820/8201b22d-aa82-4abb-9706-8cc48353cbd6/23f613f50847a69e.png)
|
| Out[79]= |

|
Compute the average projection of the Wolfram–Ricci curvature tensor between vertex 145 and all vertices with the option value "VertexMethod"→Mean:
| In[80]:= |
|
| Out[80]= |
|
Compute the maximum and minimum projections of the Wolfram–Ricci curvature tensor between vertex 145 and all vertices with the option values "VertexMethod"→Max and "VertexMethod"→Min, respectively:
| In[81]:= |
|
| Out[81]= |
|
| In[82]:= |
|
| Out[82]= |
|
Compute the average volume of geodesic tubes between vertices 145 and 355 with radii between 2 and 6 in a 20-by-20 2-dimensional grid graph with the option value "VolumeMethods"→Mean (default):
| In[83]:= |
|
| Out[83]= |

|
| In[84]:= |
|
| Out[84]= |
|
Return a list of all volumes of geodesic tubes with radii between 2 and 6 instead:
| In[85]:= |
|
| Out[85]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 2 and 6 with the option values "VolumeMethod"→Max and "VolumeMethod"→Min, respectively:
| In[86]:= |
|
| Out[86]= |
|
| In[87]:= |
|
| Out[87]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License