Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Wolfram–Ricci scalar curvature of a graph and its associated properties
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,v] computes the Wolfram–Ricci scalar curvature around vertex v in a graph graph of dimension dim, with an automatically-computed maximum ball radius. | |
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,v,rad] uses maximum ball radius rad. | |
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,v,{radmin,radmax}] uses minimum ball radius radmin and maximum ball radius radmax. | |
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,All] gives an association showing the Wolfram–Ricci scalar curvatures around each vertex in a graph graph of dimension dim, with an automatically-computed maximum ball radius. | |
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,All,rad] gives an association using maximum ball radius rad. | |
ResourceFunction["WolframRicciCurvatureScalar"][graph,dim,All,{radmin,radmax}] gives an association using minimum ball radius radmin and maximum ball radius radmax. | |
ResourceFunction["WolframRicciCurvatureScalar"][…,"prop"] gives the property "prop" for the specified Wolfram–Ricci scalar curvature computation. |
| "Volume" | the volumes of geodesic balls of various radii around a given vertex |
| "AllVolumes" | an association showing the volumes of geodesic balls of various radii around each vertex |
| "Curvature" | the Wolfram–Ricci scalar curvature at a given vertex |
| "AllCurvatures" | an association showing the Wolfram–Ricci scalar curvatures at each vertex |
| "HighlightedGraph" | a highlighted graph depicting how the Wolfram–Ricci scalar curvature is computed |
| "TransitivelyReduce" | False | whether to use the transitive reduction of the input graph |
| "UndirectedGraph" | False | whether to use the undirected form of the input graph |
| "AverageVolumes" | True | whether to take an average over geodesic balls of different volumes |
| "VolumeMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls of different volumes (or simply return all values) |
| "CurvatureMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls yielding different curvatures (or simply return all values) |
| "VertexMethod" | Identity | whether to take a maximum, minimum or mean over all vertices in the input graph (or simply return all values) |
Compute the Wolfram–Ricci scalar curvature at vertex 150 in a 20-by-20 2-dimensional grid graph:
| In[1]:= |
|
| Out[1]= |

|
Compute the maximum and minimum curvatures over geodesic balls with radii up to 8:
| In[2]:= |
|
| Out[2]= |
|
| In[3]:= |
|
| Out[3]= |
|
Return a list of all curvatures over geodesic balls with radii up to 8:
| In[4]:= |
|
| Out[4]= |
|
Show the geodesic balls with radii up to 8 as a highlighted graph:
| In[5]:= |
|
| Out[5]= |
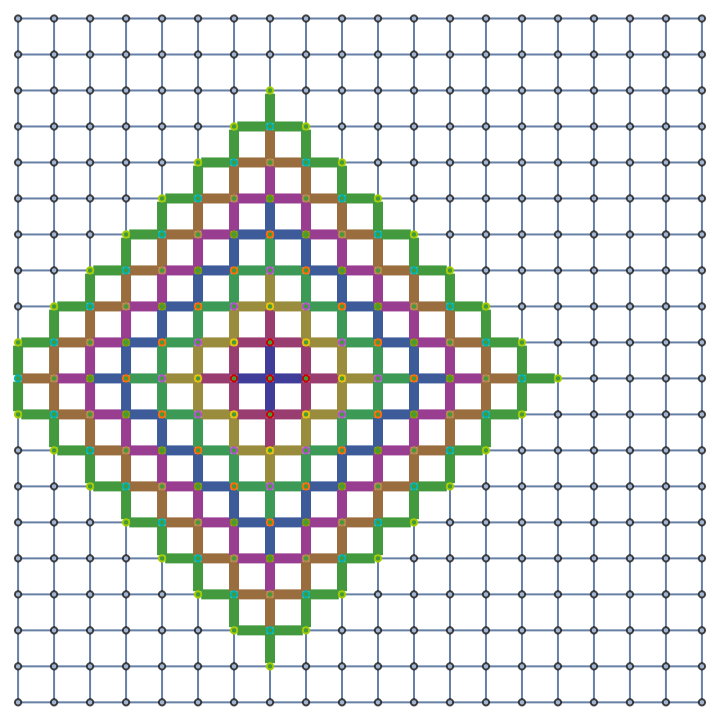
|
Return an Association showing the Wolfram–Ricci scalar curvatures at each vertex:
| In[6]:= |
|
| Out[6]= |

|
Compute the maximum and minimum curvatures across all vertices:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
Compute the average curvature across all vertices:
| In[9]:= |
|
| Out[9]= |
|
Compute the average volume of geodesic balls around vertex 250 in a 10-by-10-by-10 3-dimensional grid graph:
| In[10]:= |
|
| Out[10]= |

|
| In[11]:= |
|
| Out[11]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 3 and 9:
| In[12]:= |
|
| Out[12]= |
|
| In[13]:= |
|
| Out[13]= |
|
Return a list of all volumes of geodesic balls with radii between 3 and 9:
| In[14]:= |
|
| Out[14]= |
|
Show the geodesic balls with radii between 3 and 9 as a highlighted graph:
| In[15]:= |
|
| Out[15]= |
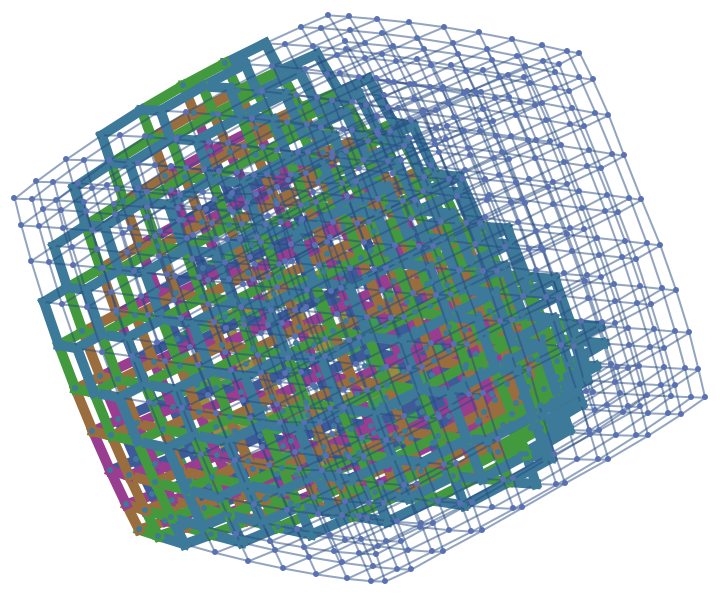
|
Return an Association showing the geodesic ball volumes around each vertex:
| In[16]:= |
|
| Out[16]= |

|
Compute the maximum and minimum ball volumes across all vertices:
| In[17]:= |
|
| Out[17]= |
|
| In[18]:= |
|
| Out[18]= |
|
Compute the average ball volume across all vertices:
| In[19]:= |
|
| Out[19]= |
|
Compute the Wolfram–Ricci scalar curvature at an arbitrary vertex in an approximately spherical graph (produced using ExtrinsicCurvedManifoldToGraph), and show that the curvature is positive:
| In[20]:= |
![sphereGraph = \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"], {Null, CompressedData["
1:eJwVxfk/GgoAAHDRXJFjrrAOaRmhJIVHZJGtVzRnLKPcSZR1keN55RoKKSJX
GipRMoqaYv6s93nfX76InlFWT2hISAg6LCTk/wd2ssYiByJ3opAY7JgOKc7o
yToYO4jUancyGrMao3KRuZsW2HieETIB0eafZPRn9Tf2J0AStAk7sOfxZ1hg
PJCwl7+Xi8fgsXgABoAF4JtEkPmJ+Sa9SA9gYVhYFp7V8AIpL58on+81gtgq
E0jKlmY8Nj72PP5zqbo0XUamJ6Sna9N3QGAwGyx9Y8l7Nb4+vp5cg1cgK+Ur
EyvzK6gilCmnN8eIGhoytc21XWUfZF/lCPIEvQKBUfAseA0rD/ua39EhRp0V
nanOTGfruvXH9deIzQhLYgOMTB4nr5N15GeQHCxny6XyMZfOdeBCuYvcKrfJ
feZuW5xbXLyCUclU6jhVR3VRAyBboq3BJrfZXiIRCAxiIOeo98h4BGKCmYlM
JpspZcqZtsy8zIbMnszHzJewWkhteW3tRO08wIPwYDxYD97D8oDMYDPTzDZL
zXJzTF5Mb4wgxhi5n7Cfvj+wr93f2Uf9/PEzcTBzsGFw0Barir1sn2s/ab9G
FRQUFZwVuJuCoqA+CPOT/VT/uF/nd/n9gZianJq8mpreGkGNseY10Zfpa/D1
+AZ9Np/vJX2bvS3d1m5vm2MXVAsLpoXLBXf+TcfN3s3JDZlCoVLGKOsUHcVF
8X+/WLy4uEpGJGOSB5LFCd353R3d3XvdN9nV1dRqUbWr2p/2Ka0jTRx5m36L
uB241d7u3O7fRrUgW3JbYqZzpvOma6Z7pwXT08bpVxAXzOVOcKVcOXeeu8I1
vzmOON48PrYkCxFCpBAjbBEOCIVi8iRlkjrZONk/OTY5uT6pm3RFKZCKXAVG
gVe0KISKtCpkVZU4CZVUkFSUpEo6S3K/+wYgfCBgCXgCgfXu82fmZ/bnbxm7
jbtfd3t2+3dj6+oW3v6GEYlkIoVIJY4TdUQ/MUB8fltc/L34N0xNVJPVFDVV
Pa5Wr6t1ar86oH4Ok0Fk5bJa2YRMNi/bA9CwNDyNQKOxaJ6osrQyZFlZVVlL
mTh/uH14+GT4Jm0NuVa2VrX2aU28llNS0lvyo+So5DmrtLS/dKz0oEkpUir1
yoAyGJ4cjgjHhA+EC8PFaXf5d5/uOu6674bv9u5u7gBQKAKaC8VAsVA8lAZl
QYVQBdSTfd52Pne+eH5+hdoY2tgwweBwIrwaToFT4SK4Eq6Gu+B+eCAiNfW4
qbV1qHWjVd8ajNhK3WobHT0YPR+9hkngEqJEJJEoJXpJQBKEaMo1tRquZkIj
08xrVjQAL9SL8GK8WC/eS/OyvB7vu9Nvp6eWhubmnmZf80tsX11f30LfZZIB
ZSgwFBmGDCrDhsFgMpwZ3KH5oe2hw6EnodehN6F3f239ddR02HooOpQcKg/1
h4fBwtbCocJ/ClWFC4UbhabCSwAOisPgsDgcHkfA0XAsnAfnhTurnVSnyClx
Kp16p9Pl9EetIldzV8tWW1YVq4CUFGwKLoWQQkthgdBgdCIa3YBuRg+ipWg5
2ob2oV8i4uNT4zfjt+KP4y1dm12nXZbQ+vq2+vb60fq5+vP6ayAImAhEA5lA
NnAQKAXKgTYQD8xj87g8npQn563wtnnmt7+Kf/36HeVIcyAdZY4qR4tD6BA7
FI5Vx5ojGhX9I3oj+mf4fcJ98j3ifuBeeL9zv39/e59kR9kL7IX2IrvKvmA3
2E32M7vdDSPBSaQmkogkISlJetIhKUAK/v1v7MiHkdyRupG+kQhGPCOVwehi
bDK2GMcMS9hM/kztjGxmZm/m5tOfuT+//+Q8lDz0Pvx4eHgGxsXExSXGDcb9
G2eL/Phx++NtRmdWZ2lnY2fn187+zt3op9Qn1FPBU9HT1pPh6edTQiWkMr2y
srtSVqmt3Kvcj5iKn2JMdU1NbU5Z4PxsfjWfyueL+BK+ku/ku/j+iIr4igpG
RVfFVMVmxXHFaYUlxpppzbPWWAXWaavRan20vgKW3iylLH1YIizRloCzcbOJ
s+jZhtnB2VnbrC+bXk2nN9H5dBFdT7+gO+lBEAfMQXOaORwuh8eZ4Eg5cs48
Z4Wj4Zg5L2+/FH/58it2+cMyYblueWT5Pf399/cX/wHrgXhh
"]}, {EdgeStyle -> {
Directive[
Hue[0.63, 0.7, 0.5],
Opacity[0.7]]}, VertexStyle -> {
Directive[
Hue[0.63, 0.26, 0.89],
EdgeForm[
Directive[
Hue[0.63, 0.7, 0.33],
Opacity[0.95]]]]}, VertexCoordinates -> CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJw1l2k0FIwbxS3tpWghW6nskUqFwvOibFmKLGmTlBbakEiRlL1SVIpsvXbJ
moQHYcgSY5+xzBgzZp9XISr5+/L/cD8/59xzz31+d4vbNbvzIkJCQk0LEl2Q
2/6CC1se8fCZ616/d2Z9eOS3WmgfIBL/lfV3d8vH4AJrw1hRAWyZvtJlsK4d
aloYYZWa56BJsSvjlxcdCp+YRdM/jQOrVrTR0xXhzchd8ZOfRzDAf0ps2J8D
Jeciy/MPU/GQiZ+sxq1xvNL9c0OxKQmpFi4RTfY83Kr5PHAqlwgBRy5W1F7p
hMb4DA0N6jtUWLMSFWk8dLcJTtkc0IsOHyRJUs9ZuH5JuuIS/3Kc3GKbN8kZ
hdNEUeouEw7uP+bqPnS/C/44Dt/XEyVjgOt8SYEcBRb/0vzhJTyMQ7vNv1N3
jmNeoI+fjVMmirm88OZyiWhfZPGCFcgH1eWW4U8f0UHq11KzqDIqqsr4JCyz
GwH9/yjKl5+NYvDZo/oV8mW4XuuDtdEoC3NL55YUelXi90SVxZM8AgZ1xHmv
3COAfQS9h3+UeuGBdh1aRNNQtAID26sYoDzpqbk3rA63N+c+a17NRz/ZV3uO
1nThnPwmqsP8KP49wtsW/5QExpbiVcJLGbA1Kq9M53snDMtlXFh+gIKa6urF
psvY4My4sOtVNhkfh5UaChPGoCIlqfTadxpOV6gbHj9PwHs6A25K62j4IjVV
4DfLRJlQAt5o42Fj4lCGokQnJHibZvE9voHHJd2Rzo1svJ8Q0j4lPYounysI
lreqsNO5JWZFQCEU1MikrhHioWg7W60ilIRxn9dKCnHG0NPYb9G97UzoJkQ8
8mqMh2RTuw/Zd7rQP3RZwhe1HjBPbFXcGMuFY8Rrk8kRNLzlPl+1xaYMWN8a
Vu3eyoJAVp1xBIyDWKQVLzWrH/YdLGWH7xmF2LL8fz4H08BnR/7pWM82rNMv
aVQDJtx/7nBOx2kYN4Ve26B4hYVOgsc6AdAPrcGJ49ffC3Ctc3nprGQNSj0v
V3uP79FIZlBPRY8HJzYExB7oqkThIcPsbdR+tNRLfFwry4UCBjc31LYJfrsm
0KUZZFyh7XZbI5yPKjvjdj21K4BlffV/1KKJcGZsRWZHAB30U3hf2rPpEHtE
od5QQISBOq9GaX8u+i2+c/6QDwmqJqrLW7cTcMXVdExbS4NNvCiLKTEG0N6Y
9ejtJGFWFt2FmFEP3uY1wh2hw6h008w9KYmDWlcsa4jLm4FkPN1TjKMwkNqn
ZrqZhfa2/+whu7fD7QYdlbKXX/EhP+g/Myc+HHCb0ZDoZUJJn8pjoeVjOP17
NL9uOAdi/XUtA2vG8Y54IM/xbD8Gvfc7sPsJFSUCSzmSzjzcVV1/aoxTAkpF
YOBX2o9W1CSrllQWlHhanmxU7EF2aQ1HvmMElnw2CokdFSC76MKXTOprdMy8
5XnLoxAiS73jPbQGkHN3RcnsBBuWJG8VBIT0QeKc3b/K5xDS5f19Gf40ZLjX
eISLsTAkRemP0OsPOLn9qcyqyx9xW5eu2FCjAKXNvpZeXci94weP6ISvnag0
naSWb9eMD0ey3oQU8NEzcwQOSXegevaqzvxURHP1ZOJMehzcimjQUPAZQ+P/
PtYejmLioFh87r82AhyWVs+Zs63FFTUaFR8yvyDlKKlDeCGHrsbz3sfyaDBg
w2K2GYxjcSfzSckWDv5ZovV91XoyNh2yTRgz6cZ1ylUhOh+ZoDnJOJbKoiGn
mf5tkXcV/mt2xe34Xj7IDPifYienoZOsogVlqBuvmlO3zb9iwJR3v52huw8O
vxo8X5jCwKIoxdrdE2PwZjpwOvAzA9otPj5n7emAuCP0PQZlLLy+SregtI0K
ugcePBPNbsarHmV5G7l+oClpP/t5sh9Mi0dWetzggcJ2HS/9JDLIqGsXXQvi
okhH/M+dubWYlukspVJJxN2lNvGFj/g4PcsTN0rNwonUQVVRw1G0MdwVVLWJ
DEU/VA9aBzBgtFJf2YMngLdOplck7dPgTXL/s6F9GWh70vCP2vFxnHAe6ste
QQed9ytdq88SsNPLDcubWXAxTHRF9lEySBgLn107NYA2Xlt2vJEWgFOiyLVP
N79CIr9z5GFcBR58qksKDmKDcphqUZ/pMJaH/xMuMUkE1TPML0GGTBQcb2oL
W9yHjqJ0d9fTVHD/5nN1aSIfXp7P2258mgATIc0T/rWtGH3BWsXHyxu7eolx
Qc4UsJbKfBbny4Gw8d72KVs6bkyfMu4YeYIN5/IlZtvGMWjC+OdCxJFH2Pha
LKMXz3SRyraXfkEfrWK31MxmmHvfQ7d2EIDz2s2nhnUjoEFFwmXrKRJ+nZW6
lyjBg+T0ZG2brbm4KqTb6KN1F/4y+DY8tmccf6cxRTqraJCu7XD97Tcq/HAc
e3pEmgL35NaMd2+iY2Fv1LKe+x8gQ2Fxn6Y1B11nWr+Y3qZAmL7cV7/2z5ig
cmjU1UiAB6tvi0RvIyBvg4F70kwprkjyvdiQS0XCNZGmzrts8MnIvOd1hgzm
hke99mm04/lwu1u9oxwIdgrbWiLJgpSaLukl//XDWW9fNcWeYeg2jShRWibA
fqHDh6jzbei877V9XVA2mj8oLJMzpuKfSD/tUy1DEKJT4VbmyUCrmDW6ixIG
4byR6otsDgHO07Qi/zI5mFWWvPdYdRdc3yB1JJ4SBlvEbFpqz/MhZWt/uuIh
Hpb9rG5YT+iEtQ/dGzNfEzH7gq3UKoNu0JIsfbBFNg42JAV+67XmYyZR3SFL
rAHsrm1Wf7mMDwR6k6W6cRcqp0uHPG+OgfurfWdMqAK4aN2SGPG5EATxNuLp
vW1Ya+287g5/BK8nRh6mpLFBtigo8eEMHSP2+t+2ekYH5esmZlThTpAotrdP
aBsDsx9Nmtm6FND3bzCUXz4Kjn7Ged+DuyH7sI2BziADmFnRCUJkGlj8o+Nm
pZ0GoczfbOWXb/D/uZfflTsrZtWMaxp/MWoW/BsJYcrLXKmFyE/ifo8MRlGe
ldA/cJWBRx4+11i6nQzWuu0nE2dGsfV7kEJoPx08//lWEryZDJnSPeNnODT4
9XdPZQLpC7yaelgfGsCE7xY95D9etdg2HZldfuYd9sqOaqlnCMAle/rGxl2d
+FAyhzHr2IgZ98jiXaYLPv9nETi0mAmXO/cI91SPIaPR9f1MTDUoXKpcHpVC
RW7KoXvKz5zg+e9yKaHshX/cqaE8FcIEGfEWDSu1YagzvZVi/pUM6rGmZzRX
cZEsta2mOqMF4gWDYvu9yaCpeZ30evEApP+S/1ImS8FP/fMWhSlMCJM8a3gw
pAXafnan5SW24Ja62J0KPnzMoilLhNk34FSq+DqXPh4IWfxnonikG9y8Kw8o
GrNA99QxxfodffBTy33yQMwILteXwFQxJv5cPS0d25GF3fYDu21/jaHVg5G/
2S+48OT5Mx9t7X7cf51+ZBO0g2oh95zkokH49bwsaG8BFzRdPfQeFuXjB1Lk
/BM5AZqZfHfg9LfAU/ePPa5VxaB9a3Mxo44DBXOTzJW5I7BP9O0jaavXoP7S
9M/3Y3z4RnTOuKbSjJ1xJdKvM77hqoqHW6+bj8P7RfJVVbuJwKJX7opf6O+E
1MKq1VvZqL+Dbvb0xCjUxOrHREe9glqhMZOZtjp0aPuh1y7dBd8b//YdU+TD
q4+rTVPHo+CqRHDMCZExaOq19ZRmMrHDVap/UScT4hqFN66XCQCbtBIn7a1j
KKluLSk2W4Oty50+eqh2YlRtbXL8Ajf+NTUK3ijfgkuCpUTK+qnA/yScdjqN
BU2X9hdv9fmEq29++PpLtxergiX01n7lwevvrN9+L/jYeunPX92zDbDJL+ro
vcftqHD2R9LFYh7MOrXPcQU90JVnY/wgrxYkVbv8X87V4KWVBaT+fAGaC/2q
M6+NgjVsq+PnbjJA4u9Ltn5oGYgaXlshiGeg2vgK1olTbNCx+70soIOMTzRe
Pnq4uQ/6BcEDtpItaKT9OVA2iAGTznuq6j/QwSX65niGSTfIU//q2IRQUCRV
LaDLiwXBjl2HpMNlIbVcz15BXQAqak4eEmGtmJMwqMyrKkJv+300Q9UGkPga
RNt5Q4Arl5+hKOh8QZfjBxLFOO2wlk+fomTwYfXmaqXEo7VgdiZnI6OTjaEX
Iz3ukCnAemDRd1e3C5XqN/iGQTd2pIfXNSMXHVyyDZ68FQDJfvjZzP3HOOP4
Kvh9QR2Kya5f+e/lflzTlKwh09yC+Z9Hve1Kubh77YWx8HkCfEru3U505MK5
U+/iNWdIqHvIaE1bKwPDuW4jCdfGMGb3PDXQi4hqqHTHNYyOp+nk7qnpPqwe
qVxXe2EMox+vOl430IxdheO1BQu+3zhkPXlyjg9B21xmZMjjkORaZ0ByGca8
yCUis+QhlNsSv6mjl4MBIe9Ji9Z1gubmnJBvWiTUityZd/keHaXshyRnhhjA
druYeXCGgKfHll5pVhSA+0Ew/r30HeiQfrx2NWuFI/wkgdiMBwz2bYvpSSPC
fmniSpU4PlzetYhwR5GGIn2ntE8oVkKsxtovtk4sGBmblRgld4KTdGzii1Xt
eKt09EFiAw+L7XPupl9D/FunMnrikwBrbpX1FHx8i4+4NPMwn3oIDb9nbCPH
QxmZjL2PFzjxNAvrKysEcL7Najf4VwOxOXmlfVQaNM9ylAx3UnDv3aos8YMd
mCeltJFsyQZax90lvjuosHybY2vE/U6wfMeJWezHwsqIvisTr56DzY4qk471
FAziHc/+scC3HcpvLM5Vj6NxqOSVlI73cKVCTETOlg4Cr49TFSo0MMqmtx4M
H4aKlyJNl2PGwFKYrhdwYxz2uZxvGowexdOuQsqHs3rheanIfH4LCVsjNtwS
K2RAmFF5JUFhFHz3r89qNBvH0kdOsn8JBNis3PtLZyMdkje83Osq/RFFrpp+
Oi7VgbXM+tt9LXx0PRZ/PAQYcHOPYfztBU5r/PMsrSbgEx7nJD9Ikh2D6TVT
FT+1cnDgXtCOd81M1DjY092/hQaXcpl3N/oumFU1aEZdXwYRkoTQmwv8WFtn
a9R3jIv1b3Pnyy70YNaOiScXhyMxYMJX+kEJDyKmPocmvuwD+0RKXrH6Nzw4
t+PCeYNO5ExOKeU088DnZF3H/eVUHH6R6HDwCxvf3x2ov36hGkzOZgltJPWh
7ROVkkouF58/JVyQjf2KNzudS36+o8CGZ1dbZrxGMDN6+V7iMQbanSzKPLuw
P2ZFXn1cSaRiTqi2rYDDQt4sJ7c3kAiFhcRNi05wwUqzS3XDTC9Wlx/ln1Br
BaXN9Mjx8jFoFOgGGhwax9M0sY6TwmyIrP9N+m3Ygdtbtf7WLtxjW/TdVFnf
DmcL2Wd9DUaw2nKlpRyJDelFUTmyh2tRlKY2+F5lCPlzDp4fNnOx1LH3zXxV
OzLnQUR19Qfsyr/2Tn+GjzH+2o5pwRzM+CftCk14BLznlBv+yH/BVO3Lg9FB
fXDAdtGiLHE2jK97u9rz3SDmiHcTevK7wDjffE1bIg+kJu78pEy0QPLsL0XT
TSwI8ZNxNbHqBXvzPZRcewoqm/o88fyXC2MDza7KFBKozv141xZYh2W02vjq
/D6k+jY8lj/MhjxFv4mwPDJQ2m/K8d80o4P4uqdaQRRMzD/NHklio1f4Xrmu
mIV9X9YydEQzCdT9+0/c2UmD88T+MQgeQB/t6P26WrSF3fCjv12NgbvtWosl
P5FQKLOMl3OJA2csdqUYK3TBwPyKH17mHKy45FPl8bsbwiPk4eTXAdjutZyi
5LCwhxo8Uzadakb1i+vrpZTiwFmVmp3dzscSEeNDbb5NON0yrKRCJsC5RPKZ
9DgmNK7VyqXL0bAiWy7yRmErnhInm9b2syBjkWi/y5lC4F6NuXgqbxT2K/h9
eMAbAhsjWw2ryibkONx/9/AJB3xiJpKPh/NBWs8k4OilchDb5lW0928nvkyN
cLh+iYj+jE+tkUMsSCu7fH+pIwUfOKYNE/5rgtvuMkIZpxZ61Oap49wPOi5e
Hfgm/hsX9vjJ2Q0N5aP8nZNrx7zJeIRC/SmtR4FdOdu9dfYTwN0PNpuNsPHR
zIChQhgfFHTSLIWdiNhztE8/Z6oUI5c085Of9sCPotGYj3GIYSkkaycyD+iP
T7y5faIb6cE9Zr4L/9D0grem3u0mdNliZnZVnAe7SmMhRKwN1+YSPLtNeuF/
taMoQA==
"], {
{Hue[0.63, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxfk/GgoAAHDRXJFjrrAOaRmhJIVHZJGtVzRnLKPcSZR1keN55RoKKSJX
GipRMoqaYv6s93nfX76InlFWT2hISAg6LCTk/wEpACgAA8ACcAA8gACgAViA
JYAH4A3ND60PbQ8dDj0JvQ69Cb0LKw+rDfsaJgubAYKAccBEIBrIBLKBg0Ap
UA6cBdreLL05fmMJTw5HhGPCB8KF4eLw+4j4iNSIighGxFTEZsRWxHGEJTI9
EhH5MXIgUhu5E7kfeRuFjMqNKotqiVJErUY5olHRP6I3on9GP4HAIDSICWKD
OCAuiAeSguQgM8gWExeTF1MT0xsjiJmOMcZYY+ti+2JHYlWxC7HLsZdgNJgJ
ZoM5YC6YB5aC5eAVsDkuMW4wbjbu3zhbfGp8RTwjfip+M34r/jjekgBJSE+o
TOhO0CbsJOwl7CfcJ6ITmYkNiYOJs4m2RN/b4rdf3v56+zsJlVSQVJSkSjIk
nSXZk9zJiGRM8kCyMFmcfJ+CTcGlEFJoKayUpVRG6lbqcepTWllaVdqntI40
cdpamiPtDlIOqYTUQiYgMsg8ZAWigWjTK9O16dvpO+n76bcZjRmdGT0Z/Rm7
GY+ZeZkNmT2Zg5nWzMdMX+bLu8/vvr07hSKguVAMFAvFQfFQGpQFFUIVUA/U
C4PDiDASjAyjwsZhEpga5ocFYM9wIpwEr4ZT4FQ4Hy6CS+BKuBruhLvgfngA
gUEMIISIW8Q9woPwZpVmNWZ1ZvVnjWUdIHORZcgqZAtSiBQjFchV5BrSkV2d
Tc/mZx9kn2dfoQpQRagh1AbKgDKhfqLOUHaUG/X0nv7++/sLdAO6Gc1BD6Kl
aDl6Fm1D+9AvOSU5NTm9OYKc6RxjzlHOwwfCh5EPSx+Wc/G5LbkjuYrc1bya
PEHedJ4xz5r3isFicBg8hoURYhQYD8ab35HfnT+cP5O/l3+Sf5N/V1BUYCg4
K7AXuAueClsLhwr/KVQVLhRuFJoK7YWXWBwWjyVgaVgW1oP14vA4Ao6GY+E8
OG+RoeisyF7kLnrCE/A0PAuvwHvw3uIvxd+LfxX/JtAILMISYbmkt+RHyVHJ
Q8kzkUykEKnEcaKEqCbqiH5igPhMaiKJSBKSkqQnHZICpGBpZ2l/6VjpQVlV
WUuZuGy1bK3MUV5bPlEuK58vXynX/LX111EFo6KrYqpis+K44rTCUtldKavU
Vu5V7pMpZCp5nDxJVpPXyTqyn/xcJa5aq3JUU6vp1fxqUbWz2lXtp1ApY5RJ
ipqyTtFRXBR/TW+NoGa6xlhjrXn9uP3xlsqnjlMnqWqqjuqkuqh+aqB2olZW
O1M7X6up66sbqVuoW6axaEs0D81b31bfXj9aP1d/Xn/9ae3T3ac/n5mf2Z+/
0ZvofLqIrqdf0J304N//MroYU4xNxhbjmGFhsplSppxpZtoamhsGG2YbbA2+
hpfGzsb+xsnG3cZHlofl/fKrqbVJ1KRs0jcdNgWbOc09zb7mlxZhi6JltcXR
OtS60apvPWwNto22zbUttp23XbUPt8+1n7Rfs3lsKVvO3mabO7o7xB03HXed
Xzv7O3e/7nK4HB5ngiPlyDnznBWOhmPmvHRNdW12nXZZvp1273XfdN/17PY8
9vi4PO4EV8qVc+e5K1wN18yT8uS8Fd42z9wr6J3uNfYe9T70jfQt9F32T/bv
DggHdgb2B24H7gdnB22DvqGNIcOQafhk+Gb4ji/iS/hKvpPv4vtHlgXTAqPA
KngWvI4ejJ6PXgvFQoXQIbwfmxzTjR2MucbV4/7xwPizSCJSivSiQ5FTFBSv
iR0Tson5iZUJzfcLiVKilxxKnJKAJCiVS7elZtmMbF6mke3JzXKbYlXhmFyf
1E26pjanLEq98lDpVAaUwWnjtHX6dWZv5mbWNuubW5w7n/vzz+X8yrxGtaAy
qEyqM5Vddalyq9fVOrVfHVA/L5gW7AuXC+7F88WLxasVzY+fPx5WHWuOdd36
4/qrdlu7o93X3m4YNkybx5uWrSedS+ffNusP9U590GAynBnsBrfhaWd/53bn
3nhktBpf92727vZv9+9NZya76dLkPnAdBo8tJ9cnN6eWn09n9jP3+dXFlfXR
+mrz2V7sbqfL6Xf5b+5u73/99ngfnh9ffS/+wO8//wGov3hh
"]], 0.04512775258949886]},
{Hue[0.63, 0.26, 0.89], EdgeForm[{Hue[0.63, 0.7, 0.33], Opacity[
0.95]}], SphereBox[1, 0.04512775258949886], SphereBox[2, 0.04512775258949886], SphereBox[3, 0.04512775258949886], SphereBox[4, 0.04512775258949886], SphereBox[5, 0.04512775258949886], SphereBox[6, 0.04512775258949886], SphereBox[7, 0.04512775258949886], SphereBox[8, 0.04512775258949886], SphereBox[9, 0.04512775258949886], SphereBox[10, 0.04512775258949886], SphereBox[11, 0.04512775258949886], SphereBox[12, 0.04512775258949886], SphereBox[13, 0.04512775258949886], SphereBox[14, 0.04512775258949886], SphereBox[15, 0.04512775258949886], SphereBox[16, 0.04512775258949886], SphereBox[17, 0.04512775258949886], SphereBox[18, 0.04512775258949886], SphereBox[19, 0.04512775258949886], SphereBox[20, 0.04512775258949886], SphereBox[21, 0.04512775258949886], SphereBox[22, 0.04512775258949886], SphereBox[23, 0.04512775258949886], SphereBox[24, 0.04512775258949886], SphereBox[25, 0.04512775258949886], SphereBox[26, 0.04512775258949886], SphereBox[27, 0.04512775258949886], SphereBox[28, 0.04512775258949886], SphereBox[29, 0.04512775258949886], SphereBox[30, 0.04512775258949886], SphereBox[31, 0.04512775258949886], SphereBox[32, 0.04512775258949886], SphereBox[33, 0.04512775258949886], SphereBox[34, 0.04512775258949886], SphereBox[35, 0.04512775258949886], SphereBox[36, 0.04512775258949886], SphereBox[37, 0.04512775258949886], SphereBox[38, 0.04512775258949886], SphereBox[39, 0.04512775258949886], SphereBox[40, 0.04512775258949886], SphereBox[41, 0.04512775258949886], SphereBox[42, 0.04512775258949886], SphereBox[43, 0.04512775258949886], SphereBox[44, 0.04512775258949886], SphereBox[45, 0.04512775258949886], SphereBox[46, 0.04512775258949886], SphereBox[47, 0.04512775258949886], SphereBox[48, 0.04512775258949886], SphereBox[49, 0.04512775258949886], SphereBox[50, 0.04512775258949886], SphereBox[51, 0.04512775258949886], SphereBox[52, 0.04512775258949886], SphereBox[53, 0.04512775258949886], SphereBox[54, 0.04512775258949886], SphereBox[55, 0.04512775258949886], SphereBox[56, 0.04512775258949886], SphereBox[57, 0.04512775258949886], SphereBox[58, 0.04512775258949886], SphereBox[59, 0.04512775258949886], SphereBox[60, 0.04512775258949886], SphereBox[61, 0.04512775258949886], SphereBox[62, 0.04512775258949886], SphereBox[63, 0.04512775258949886], SphereBox[64, 0.04512775258949886], SphereBox[65, 0.04512775258949886], SphereBox[66, 0.04512775258949886], SphereBox[67, 0.04512775258949886], SphereBox[68, 0.04512775258949886], SphereBox[69, 0.04512775258949886], SphereBox[70, 0.04512775258949886], SphereBox[71, 0.04512775258949886], SphereBox[72, 0.04512775258949886], SphereBox[73, 0.04512775258949886], SphereBox[74, 0.04512775258949886], SphereBox[75, 0.04512775258949886], SphereBox[76, 0.04512775258949886], SphereBox[77, 0.04512775258949886], SphereBox[78, 0.04512775258949886], SphereBox[79, 0.04512775258949886], SphereBox[80, 0.04512775258949886], SphereBox[81, 0.04512775258949886], SphereBox[82, 0.04512775258949886], SphereBox[83, 0.04512775258949886], SphereBox[84, 0.04512775258949886], SphereBox[85, 0.04512775258949886], SphereBox[86, 0.04512775258949886], SphereBox[87, 0.04512775258949886], SphereBox[88, 0.04512775258949886], SphereBox[89, 0.04512775258949886], SphereBox[90, 0.04512775258949886], SphereBox[91, 0.04512775258949886], SphereBox[92, 0.04512775258949886], SphereBox[93, 0.04512775258949886], SphereBox[94, 0.04512775258949886], SphereBox[95, 0.04512775258949886], SphereBox[96, 0.04512775258949886], SphereBox[97, 0.04512775258949886], SphereBox[98, 0.04512775258949886], SphereBox[99, 0.04512775258949886], SphereBox[100, 0.04512775258949886], SphereBox[101, 0.04512775258949886], SphereBox[102, 0.04512775258949886], SphereBox[103, 0.04512775258949886], SphereBox[104, 0.04512775258949886], SphereBox[105, 0.04512775258949886], SphereBox[106, 0.04512775258949886], SphereBox[107, 0.04512775258949886], SphereBox[108, 0.04512775258949886], SphereBox[109, 0.04512775258949886], SphereBox[110, 0.04512775258949886], SphereBox[111, 0.04512775258949886], SphereBox[112, 0.04512775258949886], SphereBox[113, 0.04512775258949886], SphereBox[114, 0.04512775258949886], SphereBox[115, 0.04512775258949886], SphereBox[116, 0.04512775258949886], SphereBox[117, 0.04512775258949886], SphereBox[118, 0.04512775258949886], SphereBox[119, 0.04512775258949886], SphereBox[120, 0.04512775258949886], SphereBox[121, 0.04512775258949886], SphereBox[122, 0.04512775258949886], SphereBox[123, 0.04512775258949886], SphereBox[124, 0.04512775258949886], SphereBox[125, 0.04512775258949886], SphereBox[126, 0.04512775258949886], SphereBox[127, 0.04512775258949886], SphereBox[128, 0.04512775258949886], SphereBox[129, 0.04512775258949886], SphereBox[130, 0.04512775258949886], SphereBox[131, 0.04512775258949886], SphereBox[132, 0.04512775258949886], SphereBox[133, 0.04512775258949886], SphereBox[134, 0.04512775258949886], SphereBox[135, 0.04512775258949886], SphereBox[136, 0.04512775258949886], SphereBox[137, 0.04512775258949886], SphereBox[138, 0.04512775258949886], SphereBox[139, 0.04512775258949886], SphereBox[140, 0.04512775258949886], SphereBox[141, 0.04512775258949886], SphereBox[142, 0.04512775258949886], SphereBox[143, 0.04512775258949886], SphereBox[144, 0.04512775258949886], SphereBox[145, 0.04512775258949886], SphereBox[146, 0.04512775258949886], SphereBox[147, 0.04512775258949886], SphereBox[148, 0.04512775258949886], SphereBox[149, 0.04512775258949886], SphereBox[150, 0.04512775258949886], SphereBox[151, 0.04512775258949886], SphereBox[152, 0.04512775258949886], SphereBox[153, 0.04512775258949886], SphereBox[154, 0.04512775258949886], SphereBox[155, 0.04512775258949886], SphereBox[156, 0.04512775258949886], SphereBox[157, 0.04512775258949886], SphereBox[158, 0.04512775258949886], SphereBox[159, 0.04512775258949886], SphereBox[160, 0.04512775258949886], SphereBox[161, 0.04512775258949886], SphereBox[162, 0.04512775258949886], SphereBox[163, 0.04512775258949886], SphereBox[164, 0.04512775258949886], SphereBox[165, 0.04512775258949886], SphereBox[166, 0.04512775258949886], SphereBox[167, 0.04512775258949886], SphereBox[168, 0.04512775258949886], SphereBox[169, 0.04512775258949886], SphereBox[170, 0.04512775258949886], SphereBox[171, 0.04512775258949886], SphereBox[172, 0.04512775258949886], SphereBox[173, 0.04512775258949886], SphereBox[174, 0.04512775258949886], SphereBox[175, 0.04512775258949886], SphereBox[176, 0.04512775258949886], SphereBox[177, 0.04512775258949886], SphereBox[178, 0.04512775258949886], SphereBox[179, 0.04512775258949886], SphereBox[180, 0.04512775258949886], SphereBox[181, 0.04512775258949886], SphereBox[182, 0.04512775258949886], SphereBox[183, 0.04512775258949886], SphereBox[184, 0.04512775258949886], SphereBox[185, 0.04512775258949886], SphereBox[186, 0.04512775258949886], SphereBox[187, 0.04512775258949886], SphereBox[188, 0.04512775258949886], SphereBox[189, 0.04512775258949886], SphereBox[190, 0.04512775258949886], SphereBox[191, 0.04512775258949886], SphereBox[192, 0.04512775258949886], SphereBox[193, 0.04512775258949886], SphereBox[194, 0.04512775258949886], SphereBox[195, 0.04512775258949886], SphereBox[196, 0.04512775258949886], SphereBox[197, 0.04512775258949886], SphereBox[198, 0.04512775258949886], SphereBox[199, 0.04512775258949886], SphereBox[200, 0.04512775258949886]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
ImageSize->{320.3671875, Automatic},
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/5296b2dd0318b8c4.png)
|
| In[21]:= |
|
| Out[21]= |
|
Show the geodesic balls with radii up to 6 as a highlighted graph:
| In[22]:= |
![ResourceFunction[
"WolframRicciCurvatureScalar"][sphereGraph, 2, \
{0.06448108156822731`, -0.8531712722406339`, 0.5146821808082329`}, 6, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/18d5ca559b8367a4.png)
|
| Out[22]= |
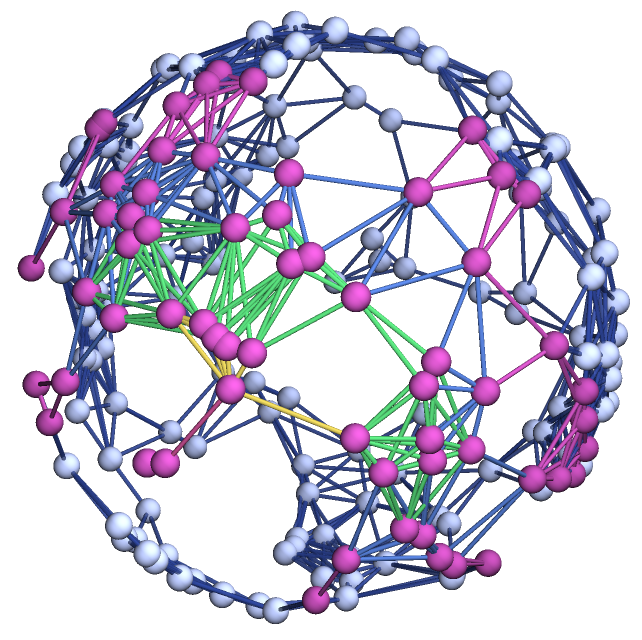
|
Compute the Wolfram–Ricci scalar curvature at an arbitrary vertex in an approximately hyperbolic paraboloidal graph (produced using ExtrinsicCurvedManifoldToGraph), and show that the curvature is negative:
| In[23]:= |
![saddleGraph = \!\(\*
Graphics3DBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"], {Null, CompressedData["
1:eJwVxfk/Gg4DAODvEjmGcktsUo7lzLHSNCpCSZRJUqQYJUdzRJdSjgxLOWoS
uUWInNNY6M96P+/zy5PK72/kA/7777+FoP/++/9IRdgbvDG6vX0vLC/vDY5C
NUZvRnuQHoUnLCIiL+ItMDqwPXAv0AMIA0QA8gBvcGlgWXRZ2WbIW/8fIBKo
AHrgEokUKEPKimQyhcwDJYV8Cykv/1b+1jAKNZKMkiXpUlJD0mj0eNn4+CZ8
RbIiXVlaATKZTUwp3IlyNjolTjqT3kQfBYxEjBSTQvbD9iP28/bL9/ff4GvM
NcmadC0Jg6FjGjBMjBSzhFnrv7j4A6gKq4qoyquqGoF2dRmBucjcXGauLFeR
NIQZahgaWgr89Kn90x6wBlmTW1NzEbgbvVu2O767uQsVCLoEMoFCYBTsCTz0
NmZbUxvcj/I3+p1++nHTcdsxVF+kF+i79DK93hhyl3pXfvftLiQlJTWlPOVb
yh10InViwojh0/lMPl/Cl/KX+Cv8teDiYFLwHtRQZOgy6A0Go+EOiEPicnG4
GpwMp8B5YqGxxbGk2IlYI1CXqyvS0XVNujadTKc7Rvbiemt6e/t7L4KrY6uL
q0nV8HvUfeO98/7eDzxCHuUe4Y5qjphHsiPd0dpRMB6Kx5PwAnwXXoE34vci
eyP7Iy8i/8RaoBa8hWSptggsXZYJi95isBgtIYUphamFheWF3wrvIs9rznvP
+8/PL87/YKb505LpoWnp9PTS9EpSBaaioqGCXzFUIa2YBqyHrUesV62PrANN
uSa8SWDqMslMCpPeZPIEL+IXSYuCxcW9otmm2bZZ3ezsMSo/vzHfmX+f/yff
/y72XfE70rvq9/9G/yV9/NjwcRTqKHIIHF0OmUPh0Dn0DoPD6DA5AIlhiRGJ
iXmJVYnrifuJb7EDxQPVAwMTwdefrvHXpOvF673rr5KvQ1+nvy59XYFjUdh8
LLYG24hdwzqx91g/dKZoRjDTNaOfmTHMGGdMM5YZB5yAIuQTsARCI0FCWCE4
CfcEPyA+LD4+L74ovim+LV4XPxt//Pnr54rPQ5+nPy99XoklQ8kkMrma3EUe
IE+Q9eQZsoFsJFuAz8jn3Gfcc81z77PsWfF89Ox5DryJvim7Gb/ZvNm9iVcX
qdvUMrVap9arZ9SzapPaEZYTn5OYk5OXU5RTnrOf8wZ/QD3kP2AfCA+ND86H
+4cHfyYqMz8Tm9mY2Z/pzDzPvMi8z3zI/JPpD7uKv0q8yrnKuyq6Kr/av7p6
i94o2xjf2Njc2N24AWRkVGWM0JuZzU3NzW3No8265tnmY6AIKcoV4UQCkUgm
UohMIo/oOSUtNS2tMI2cNpFmSLsDLGcsVy2PLL//+fMfkIfk5fJwPDyPJ+CJ
eDKegqfnmXgOnof3HHuWepZ2Rj4bOJs4M5wZzyxn0Ydlh72H44cbh5uHu4eH
N8EdnzrwHbyO9o4OQYeiY7Fjr8PTcQ3UIrW5Wpy2RsvTirQyrUKr1WlN2iOt
R/sc2dPT29Pfc95zEcjAMxg8RjujgyFgiBgKxiLDxNhjeBjX0adlp+OnG6eb
p7unh6enN+9///z9+1/S4OdBzGDFYMMgf3BwaHA68Db6tuy2/Xb8duN283b3
9vD29NZze3P7+e/Xv5K/Q3+n/y79XfkbP5UzlTdVNNU2pZ6a0k3pp2anHFNX
SUqMskJJVzYomUq+clApVSqnlWvwyq+VhMpKSeV05VLlSuXfkOTE5OSc5PLk
b8n7yVfJbynZqdlp2dmF2RPZhuyz7Lt3fcF9xX34PlJfdV9HX99i3zUQDIaC
c8FFYDyYAeaBBeAusAgsAyvAarAWrAPrwTNgA9gINoEdkZpoDVKD0/RoejXj
Gs2GZlOzqznUnGo8mhvNLZyaSUVR86lYKoFaQ6U2Up3Uc+oF9Z76QP1D9cc/
JT/lPOU9FT2pn6ae9E+zT46nq6ent/cfPvz88PvDvyQYDAOrgNFhDTAmrAnW
DOPDBmFS2ChMCVsLrI2uLautba8dr9XUbtRu1u7WHtae1t7U3qbMpc6lzWXP
Fc6Vz32bm5mbM8zdAc1gM9Kca8aZmeYmc7O5zcwzi8wys8KsNmvNOrPJbD4y
H5ufgTQwDUnLpeFoeBqNQePROmgCmogmoyloWpqeZqKZaQ6aJ5Qe2hTaHNoW
Oho6G3oM5IK5SG4uF8elcbk8roAr4sq4Cq6aq+XquCaumevgHnE93OdwaHha
eHZ4UTg5vCtcHa4PnwmfCzeEG8Mt4Y7wu/AnuBAlzBdihQRhpZAqbBQKJUKp
cEW4JnQK74UPQj94OH64aLhpuG2YOzwsG1YPTw3rhvXDs8OmYfOwY/h4+Clk
NXw1eTVlNW01ezVntXC1fPXb6tyqYXX1avVu9Qm2hdmq2KJvMbeatpq3+FvS
LeXW2tbW0TtbsC3WBrUV2/A2ko1sq7Z12fpsA7YJ24zNYFu0GW0WW3R9WX1t
fX1v/Xi9pn6jfrN+t/6w/rT+pv428lfPr/5f479+bf46/HWa5Ia5P7ox7go3
3d3g5rsH3UNuqXvUrXRvuaNjYnAxZTG1MfUxvTHjMZqYjZjNmN2Yw5jTGE/M
TcwtkBXKimflsugsJquJ1cxitbG4rGGWjKVm6VizLDNri3XEOg78Ef3j04/a
H+0/fuz9uAV0hnVGdCZ25nVWdXaOdK537ne+vcsKzorNgmZlFWeRsshZ1Vl9
WYtZxixLli3rOukSdvnxEnNZcdlwOXg5dDl6qbx0X4Ye0A+aDpoPWAdtB6MH
swcHxwB0GDoCHY9ORGegc9B5aHQVuhM9gl5Gr6Pfkl4+v2Bevr5UvDS8DL4M
vUy/uF8uX0DRoBgQDlQGqgXVg3pAvaBxkAa0AdoE7YIOQaegG9AtnIgi5hOx
RAKRWEmkEhuJQqKEKCWuENeITuI98YHoD/XCvBgv3cv0NnmbvSxvm5fvHfUq
vTrvmnfLe+A98h573d53QUGxQVlBxUGkIHJQddBA0ESQLRgChkCgEDyEBKFB
GBAepAMigHRB+iAKyCLECDFBLBAbZA9yDZwETUZOIidxkzWT1Mmeyd7JSc3k
+eTF5HPo9vvtD9v07abt5u3R7Z/bv7e3D7aPt73b/wLZIHY0O4aNZOPYtWwa
u57NYLN5bBFbwdawtexd9iHbw75h37Kf4RwUB8shcIicSg6Tw+FzhBwJR8pR
cpY4K5w1zhbHyfGHLCQvpCwULpQvfFtYWF3YX7iDy1HyfDlWTpAT5ZVyqrxR
zpEL5RK53Cm/lz/I/UmPsMePjxWPDY+Dj6OP24/ux8tHMAVCgVLwFAqNwqBw
KTxKB0VA6aKIKDKKgqKl6CkzlEWKkWKiWCgOiie+rqiurqmuuY5V11Y3XCer
U9dN1enqZuvMdY6647onuB1lx9oJdqK90s6x8+1Cu8Qutcvt0/Yl+4p9zW53
2u/tD/a/dn+SGCb+KMaIK8R0cYOYLxYPiofEUvGoWCneErvFl+JHsVf8ktQN
6/7Yjemu6G7o7hZ3D3YPdY92K7vd3Zfdj90vYBfEhXdRXDQXw8V2cV08V4dL
4BK5ZC6FS+tadJlcey6XBzAWNhYxljiWN4YeqxrrHBsZG1sf2w+Ki42Lg8al
xWXFkeLIcdVxXXEDcRNxhjhjnCXOFncGCAgIC4gISAzICMgLQAdUBXQGjAQs
w60oK9ZKsBKtlVamlWPlW4VWiVVqlVuV1mnrknXFuma12q1bVqfVH/j90/f2
799/fN8DRoGiIqOikFG4qJooahQ7qieqN0oUNRmlidJGnUddRD0DdgJ2wnYi
dhJ3MnbQO1U7nTsjO2M7yzvrO/CCzAJUQX5BAbaAUEAsoBY0FggL5AX2AmfB
fcFDgR/mg/swPqyP6KP7mD6Oj+8T+iQ+qU/pW/NZfXbflu/I5/XBEYhMBAqR
jyhAYBE1CCqiESFEyBFOxDniAnGPeED8QfiDWyGt+FZKK6O1ldfa0Spo7WtV
tC627rW6Wq8DvmR8+VL1ZeTL8pffkSWIksyS/JISaklPSX/JeclFyZ8SP6Al
oCWsJaIlsSWjJa8F3fKlpaqlpbNlpGWsZbllvWUn9DX+te6V/tr02vzKem17
1b3Ovm6/Hrwev3pfAfMB82HzEfOJ88nzOfN58+j5qvmW+c75sfn59fmd+f35
q/k3uAqlylcVqLAqgoqoqlRRVY0qjkqokqikKrlKtaJaU1lVdpVTda96UPlU
fuAJ6CTyJOoEeYI7qTlhn/Sc9J6ITiZPNCfak5Pzk4uTZ0B6QHpYenpGel46
Ov1LelV6S/pI+nL6TnhpbGlcKbQ0tTStNLu0lFw6UDpROldqKDWWWkptpWel
d8EJkISErAR8AimBkdCa0JEgSOhLWEzYS7j+Hz/fLT0=
"]}, {EdgeStyle -> {
Directive[
Hue[0.63, 0.7, 0.5],
Opacity[0.7]]}, VertexStyle -> {
Directive[
Hue[0.63, 0.26, 0.89],
EdgeForm[
Directive[
Hue[0.63, 0.7, 0.33],
Opacity[0.95]]]]}, VertexCoordinates -> CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"]}]]},
TagBox[GraphicsGroup3DBox[GraphicsComplex3DBox[CompressedData["
1:eJwNl3c8FYwXxiOiXk2hV4mIFCUKSRwNbUVK0lCi8DYk/WSkrIZEZSu0yF5Z
WcdeV9e417jm5br3utuIZP788fx7/jif83yf52yxuX/OTnjJkiV1i1q6qHG5
plMnngrQqmdLh8HdMvBqbuw/484HneiLx95f/wz31gzFxK5j4X1hKUXXcBqe
LJrcaF7fCAUMrYb7ISwU6aglaTQOYsZ/O1fyG3+AhgLN1XKgCU5FGuy6vCoN
M3YlbNumwMAtfhwXojwb1qtFrr2uVIduHwniIgQ+ToqcLXn4sRoPmivtpSRw
wcnffq94Xy366k7H2nYxQeGI7/PVn6iot6ovXv87G2n9vINa0l3QHOHAj6JQ
4bfM2Xe1+9j40Vda8ENIgDXCBy4oyrSg2Qp+7XElKpxXe7Okorwfb3C/7Or8
8Qz8vzgcfdFegumrDjKtD7Nwp+1j/hYvGsZNLfGZmeNA6fC92MSDfPzVvfW4
pnMZKtqIbpfkDKJDSWpGano32rz98CmzqAqWlrnqS0434J2CLxyCMw+fEoSk
b39koZdTntzjYDIY1kmrWDguznPUzpfWGMLyrt7dh/6SkCtcmTj7Nxi8Zu59
dxP6CYK7V7c/49JQ0Xlm2NC5Bcwljz93mSWBYbzK2btidbDGQm5u6vcgtIfk
RZgpkTHpxD9Gj1dTcVe6tnfyLjaclw4IeVXchUPhNtsjZltRdc9myQ9uw8B7
MXaxq7IfOyjFx1VreCj708EtQJSE745MSH/tGobxVu/9AQ842NPcEx75jIyZ
SmfNHhkNQf2jW7mCtEC0YwYEtFT1o2jarjcf3ZrwgYTOtR0pLBRnNlt+C+qG
JTvPmuw17QWDa5f83ISb8VjRxh6tB2z8neH1ILeVhtyACk5b+xBSJo4+dPCs
wF5CpfQVAgV8660W5uY5oGwRbqKQRcRb5LFjcwkM6D59VoYYOgS3k6zndwaV
48ZPbEePoxQYza7xQFUa6m3PnPfS4mDMyPi29ZodOMIcCZrhCTD4zd5Mv2kB
7p32y8y+YY/X38Gql5v4sHR9TnngTgG6OoV0HtHJRI21Oan/1AmgMiLa4cPB
IXS0qrah/RyEhXWKF+mVAryf+2Dj5gMsrFOOtFY+0AET2jY+U9MMOONt0nj+
7SBYdQr3yEzVwPJtw6MWuhx8QXAf35UyhGnpzhKHo0jwtbd1UNucDpORjfco
FmzoO5i6Ybr3F34NzvfPTYgC91TVPzeDKUBUTe1ZalmFf132r1w4TobOx0bG
GiJstC86eXaKNYCTZ5QSn/t3QwNBb5XRBT7+FfPzliIzsOr75aKUrUy4+t3C
jD/OhS/ys0GDzFZkBhMvsvo5+Ofq+keW5eVwlPWhWPwLE+41VF3LDuIhYR9l
fVA/Gw4Qe1aOt1ZAUHCWjfFxLnRkaBAf1rDBfMbzzorWHPCz82KK1XIx7Bax
W7KGgcZ9E4xRUxI0Ew+viNam4LqfziW3XBgYONo4NvWqDc3sColSDumQ/ccx
fVqmBmy0X515ohyN91orSkoZRehfUbKMrMJEgvFbrXZzKr7T2E3ZeJcLftBz
KziLD/mUm55jRWU4kD1SLmLPgzPDlZ/n27mgVRCppBD7CWY15z74jzwDuW7t
1D27WRjadDovrImGHy44OV/u5qGgbODHjVguLhN2HU1VywbCkrEVjv8josiB
y0Gf9DtxHfP54L2teTi+tWNWVoiPU8bp8TGrSiF/TZDC6RQOHIjcQeCvYUKj
uJGoqJQAxEzy/ye7vhtPtH8PTukQQG7WefPE10Tgjy1ViO/mgbp/a7z1hWFg
qE6oaXhE4tUDFV6HXQfhqby7q1syHUJPEp0574cgiP5QNurSd1DREvb4fouL
ox5uW2ZDqRhlYkevCaPCittv/PgdqTjLUpzuLu2FuhWe1hHGBFyiUni16C8V
xqgNcXOGfHQQX6FnEUzDF1firpU40PDUF+FAe20ByHs2xbqnDOLAtV/5jDc0
dDrYeiRHvQk2DA39PCpJBiPBDvMpAwGMG9Sai7t3gmnw2crLv1iwtq/Y5K0c
C6c1KW2fV/FRx+5I7GmRFozyth5R8WPDv7Zcso5DKVI8m+77PaKDx6ry25Er
eZBt9vxddvAwtEfam35WJcK/fwwVx8TZsObM16N2hCGY7gwyGvtIBDUF3iXj
9Ys80bCSOLOvEtwPrTX+rMQAyfoJX6q6AGLmv/76wKHByLGSqsk/A7Bn681K
6/QaiN14a/nW91wUMlw/keQ1jAmm9y/NpDGRavw2i5FBRAeubfMp/X4o7J7L
XVjOw0mKttqIRy4sN578n/YGNjzeKr6/zqIdst9OLNwNGIDJ5Vh5u6cG6d/c
r+vqDaBpz0LIt2VcIJCwmxDWh50RMTl7I3pQ9nr9rHplLdidGdsUrloN3oME
2cA/NCBrUF9uyGJC2H8bkwPMq9BRTm/T+df+UOabGPM2rRN1TjmQA+YrkG1y
U84+pxWV6c4EU7FaWPlA3t17aQrs6P0u+ySAhB7CTifAmwVZ/xm3B1gM4J29
MYqnyqhwOqtmT9NYAz4/u/N8iO0v8Jj69vrCZw5YmpSVV+uTcDCSsiZsagg+
zVlmKrTyoVXrEqFykWd5o8Vav6PjwaQqjtUVMoAhPmUZzSY94K1mKSutXAQz
7ygqwZq9IOVFdJPO+QErQ1Pi7Sj1oDv1/ILL0XYoVgs58HofCXnP444nrY6D
He/lg0NUuJjOzlLpDRLgSO2ljc8O1aOly0TkntluqD58aEEtg4TH30XFa34r
AN2gn5094c3g+HeD1MuQBjRwbbX8uSQKFD6+CA3+UQx0p7DxjFEOptOf/3Cf
ZmKiqYOPd2gratuF/fvQcxCKPG4nkQeaMOv00un7Gxn4uOD0kY8LXeD5flWl
8A4SrLM9UOIZR4doM+uSWM9uUP5cmCx6vgVUdW/2elu1AMWh4UDkMxI2+2/S
oaeGYE7e+7JRk3iU0JbwaRkrAxdmqegpryBcHluhhbpkzK7/vXZCuAXWGjED
ODti4HdUiEjxo2F0EFFv9EllgfWZt3oMrXS8WN290P51CGn7SBs+5vSBk/iF
RnZVLcRrPHVx+ESHuH4xQ63mCrjsKHVNpq4bNn0P0OldVoNNYtU7Ap9wUUq3
8qGV/TAee7RqdlynHyUTCYcOmP0CaiZNWS21Fu4kDZqKmS9y4+305Zu7hyA3
wveKh1AtbJd/beLybRDZxZpt6FeBJGFOxg0LMshfv1Kw4gwHDh+7FGgx14wB
Ps3BMaJ02M8+2HatnI8xZ7yf9A9xwUXmXYxeRBG0nM00u2rUClZ+xgqnbrBB
vveqwzJpGholBzxrz6+Cf24Ye3alMIA6o1xFNe7DmrZkzm/PemSs+92y2rAT
zvs3C247FSI1wU75TwILJKNWe5fkNiDDkRImuZUGEUdo8+dEuLjz7tKKgh+d
MNYuEkStoEHuU0q8mCgX5r9Mm5hXUKFJ90lVtUs/iF8j/um92weF7yn/KS36
XrrCtFdKnonOmeF5t8UFeJ3je5txsQP5h2bKxhtZIBOaHewvwQXn5GVHX9lW
4hEJ5za9DiYIud68dDWJD4lPOiPlUrOhMSgkZVqZB3tDQ/fbztAhT6ZQTt6R
CJJDCR+zH3eBHj3z+n7g4njIiWWyI4v5smH67fuZSvyzts7my4VSHHjSnj8q
RsKwY/6aUbHZ2Hm562q9az2QiRnmdhQBphGChTde52M8/1hkghcLLJ0lyBLr
B/Cf/04Tw2zbwbieecRetgoXWq4aZ5oK0NHhwUhcMw/lqkI1DaeqcPZlrkPL
+Deg1ATIuBZFgtKd6YWA3y04OTUR8yaZC/8WJfaOKzLR/olfpIkxD43T1gkF
JXVhcjTZV3IvHU4+aFmgLuNB54T+yZx3LJirDWT+DKiFd7KcWKNsEtrUFGdf
NmuFtbmVTpbkAEgUUXeXptOBerG+tHfcDAMEPKRxemEzb7VTxzI2KJ131X6d
MQQrk1/a1WxqgmWn9in2UmpwqE11j/dHMn6y3RXHD81GUWpJ4JISAjifrPSu
fkWD788Ukmo7yWjI+E9jbX0Zll85Zj3VxYDLkk91jwb2o7rhTKqGZyj+z2it
psauJpDW0LK0mkvDErFOLWL84h4UCko7EnsxV133vuHWOgzvL5bT0f8J0Q6u
ydJiDbj/hZVm3O1PGHpDe2IurwuF9TccE5UhYFL8B9bNiDJw9HHL/TTPBYfk
A13S8m0gMToVrFTGgDumd3srh6no7y75wju8GWumMsy2KhLAuC79QN7BWvD4
PFexWa0Hg4g+ftHvq1DGhsjNesNA1qHMx7Lbh9BGhtcxXPITyH39bxaAhpfs
TS5wa9vxdxKSSRJEaDY8FHpyuAF1Xczr+6LZuI3TOVb9bQjz+7X8tLdxIUZ4
fkJ9gYt8xvkqsdWJ6Cqte/dmDBvl2qQ2e70RYOZbCfUETgtSSVae2cnDGPZk
jeQIuRMo9ksnk8x6IPGiptGNZB7EKYWbpGl1w/oKaW/7VDokl2r4ihoUgPCp
h+Zr9AXgW53T5qfKRzLL51q2MB0VXw4f9kypwl71wq88OgUcX+BvaScKSKza
yDyyWoBzg+lJKLHYy/8NNRTaScbOVxfE928vAQYpqPwPPxeKM26JPIwsgOI9
BkVi4QngKizSM538GO6GOeiE/McDlVNG10Zu9UPYpaEEiiUN5JSL36SeGcKm
wjbpUDsGtqRUFBzckIcOyzcsl5SlAfFaVaGKVSt4S5Wkf33eAofb0m+rOmTj
rbLQzSruAoxcu+7Nyxo+ui0cjZPSZ+DUJg1lhcFSFAqwaC2i9QJXT96/+gED
Imps7tYa9YD6GaGBtNlWqIndXvDUgAXtBn8P0Yhc9LtJ+HJocx0OaqxXfB/V
h/kXhjd1X+TDSw3JwMZ7dDxf+KjKJXAYjST/6jzxTsZjXlGXgooHQTW2zf/o
znZ0h4qzj8X4oBZR9evD2WEUsl7aYBA9DMWaSelWkgMgUY1CujEkUE6yvqAa
NwAnHW/cGaJ/AcI6w5VtJ0hAeFdzRWucDj5fHowo9tFwkNQlq1yfC/toz+79
6WrDjnlrw7DiOpSsTIke0MgBk3Muqvv2lcATqU/jhbV8PHFl7682TR6GGbmT
GTPd2Hy5Rbj1fxywsCFMZd0ZwKUnDkfoWw1j7NV/jlCShqCt8MWa8pQqMGhp
36azYQAXzMTH7njyMfhH3n0xNg2XWZ1TTHvUDxErWhYPjYrLpVW2qKfGYItt
FXlHeAvG1PkJiatxIHuQCqrxQ/iqOeMVf6YZghr/dv96Xg81tbN77I/EgT/7
zqybXht8K99bcUKNgj6PEk0OpSSg/BK2ouRtDvA3FJWjEwv2t4kUPtYohNaU
8wdfPa2GyfeuHxZ202DeYbnErq1tSEgizHctENF/SsZXSpkLU7a11do9DFy7
+Vy1jFIvllifkLqb2wY9vXK2fvn54KXK/XQwnod6Pw11Gq4N4FmFpgCZhQGI
UjchpHxdzHu9AaeL+cPAPrVCJVevC/0OEuhZXt2Q/iNQf08BGy4ur8/pvEFF
ge1o3y8fFuzz2x1xL60Olym3RO9VpcGwUm+U7aK/XAidtZk2JLy7Im/oeNAw
+PR1v/aXoqCCQ0xTgwkDfRmy5y7vb8Phldv62q60IWv/Gr3ZO32gKnRp4Jla
CeoW734RuNhjtTt++/3up8L3paOU8r/dQPJVkWUtoWLK6LTK/VEOTG4p2Jlw
iYoxiidufNEfROdDb1+892dDr+bqc50qHWisse10oyQLvy8TbLfUZmJAJCWu
rjQP6DtftiR58WGqwZGj7c2DYrre4Ttv0uBkTPvpjA0CcEPzZ3GJPKCnsGZL
unMhvwhLtz1lQstEpo0OQwAd+oqVn9b0oounjUVGORcG9m/uUwkfwKR/ZKBg
FxW6ulyTHopQoS6B4nz7ei2GXbTg5pUSINpD3CB/WgA664lHWY1U8BaVpDgr
MsEnU91aPbMVJe+bFPFKqDhfndM4PFuL2aI20yRAuBmxbd3JfAo0m5NMNX9U
4C4+55DNTy7sjfrxbJckFzHO8Ibbvi/ANTQVNStc/IeEtxTYPCLCJO9D/81j
rTBVZNZZxBIA6VH09ZGOJJwhn2p+XyqASXlDRrJ4N7ygJ7Rq3uhDA70EevaK
RGRmJkYdJ3Th8CvPcdksNnqsC3ca+EhFisgJla3yHHCZGHCKc2ZDzrGkpTqD
n+H/8+hBHA==
"], {
{Hue[0.63, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], Arrow3DBox[TubeBox[CompressedData["
1:eJwVxfk/Gg4DAODvEjmGcktsUo7lzLHSNCpCSZRJUqQYJUdzRJdSjgxLOWoS
uUWInNNY6M96P+/zy5PK72/kA/7777+FoP/++//vgt7Fvst6V/yO9K76Xd87
GyAAEAaIAMQDEgHpgAxAHgANqAK0ADoBI4AxwDxgGbAO2AG8BYQFRAQkBqQH
ZATkBaADvgRUBbQEdAaMBMwHLAfsAMHAKCASmAvEAWuANCATyAJygTygCCgD
KoCTQC1QBzQBzcAj4AnQA3wOjA78FFgWWBvICGQHtgd+D/wRuBu4F+gJvAm8
DYoNigvKCioOIgWRg6qDBoImgmygKFA0KAaEA5WBakH1IDaoB9QLGgdNgjSg
DdAmaBd0CDoBnYJuQLfBkOCE4Kzg4mB8MCm4Org1uCO4L3gx2Ba8F3wdkhyS
ElIYUh7yLWQhZDVkP+Qu5C2UHtoU2hzKCm0LHQ2dDd0OPQg9DvWGvoZFhMWH
JYalh+WE5YWhw6rCWsI6w8bC5sPWw3bC9sOuwt7ef3j/8/3v99vv/4VDw9PC
s8OLwkvDyeFd4epwffhM+Fy4IdwYvhpuCXeE34U/RSRG5EWgI6oiWiI6I0Yi
xiLmI9YjdiL2I94ioyJLInsieyP7IycjNZG/Ik8izyMvIv+AIWAoOBdcBMaD
KWAamAHmgnlgAbgLLAIPg2VgBVgN1oJ1YD14BmwAG8EmsBnsALsgCRAoBA8h
QSgQGoQBaYXwIB0QAaQL0gdRQBYhRogJYoHYIHsQF+Q6ChmFi6qJokaxo3qi
eqNEUZNRmiht1EnUedRF1HN0THRZdG10fTQ7uj36R/R4tCZ6I3ozejf6MPo0
2hN9E30bg4spi6mNqY9hx/TGjMdoYjZiNmN2Yw5jTmM8MTcxt7FxsdDYrNji
2NJYUiw5tjp2IHYi1hhribXFnsVB49LisuJK40hx5LjquK64gbiJOEOcMc4S
Z4s7i8+Jz4tHxxfF18U3xbPi2+KH49XxU/G6+Nn44/ir+Kf414SsBHwCKYGR
0JrQkSBI6EtYTNhLuE5MTsxJzEtEJ1YltiR2Jo4lzieuJ+4k7ideJb5Bs6Cl
UDyUBCVDKVABtAs6AdVDZ6AGqBFqgdqgjiRY0sckTFJFUkNSd5I4aTBpKGk0
SZnkTrpMekx6gWFgFTA6rAHGhDXBmmF8WDdMDBuESWGjMCVsDbYFc8MuYY8w
L8yXnJNcnvwteT55IXk1eT/5Kvkp+S0lNSUtJTulMKU85VvKXMpCymrK3Yef
H35/2P7w72PDx+6P4o+jH90fLz8+pqalZqcWppamTqTOpZ6l3sERcBS8AI6F
E+BEeCWcCm+Ec+BCuAQuhcvhKvgKfA1uhdvhTvg9/AHug/vTstMK00rTyGkT
aXNphrTVtLO0O0QmAoXIRxQgShBYRA2CimhECBFyhBNxjrhA3CMeEH8QfmQu
EoesQdKQbCQXyUP2IkVIGVKBnERqkFqkGXmEPEF6kM/pGel56ej0L+lV6S3p
I+nL6TsZ6IwvGVUZLRkjGcsZO5mozPzMgsySTGwmNbMxsz/TmXmeeZF5n/mQ
+SfTn1WcRcoiZ1Vn9WUtZhmzLFm2rOtP7Z86Pn3/9OPT3qdrVD6qAIVFEVBE
FBXViOKghCg5SoWyouwoJ+oe9YDyZxdml2ZPZM9lG7JXs8+y73LyctA5RTnl
OVM58zmrOfs5VzlPOW+5uNyaXFouM5eVy83l5YpyZbmKXG2uLteUa849yn3O
Q+dV5bXkdeaN5U3lzeft513lPeW95Rfkl+Rj8wn5xHxqfmO+MF+er8p35t/n
P+T/yfcXYAsIBcQCakFjgbBAXqAqsBc4C+4LHgr86Cp0C7oTPYIeQ8+jl9Hr
6B30W2F54bfCucKFwtXCu6K6ouEiWZG6aKpIV6QvmimaLTIUOYquip6KScXV
xX3FA8W2EmpJT0l/yXnJRcmfEv/nr58rPg9+Hvo8/Xnp88rnv59fMBUYOqYB
w8TwMd0YMWYQM4SRYpSYacwSZg2zhXFjLjFejA/zgiVgidgaLBXbiOVghVg5
VoVdw1qxdqwTe499wPqw/lJy6UDpROlcqaHUWGoptZWeld7hanA0HBvHxfFw
vTgRToZT4CZxGpwWZ8Yd4U5wHtzzl6ovLV9Gvix/+V1WW1ZfNl62UbZZtlt2
WHZadlN2iyfhKXganoFvxfPwHXgBvgvfh1fgF/FGvAlvwdvwe3gX/vpr5VfJ
16Gv01+Xvq58/fv1pfxb+Vz5Qvlq+X75Vfld+VtFQwW/ortCXDFYMVQhrVBW
TFdsVbgrLiseK14IREIlgUpoJHAIQoKEICeoCCsEK8FOcBLuCQ8EP7GSSCU2
EjlEIVFClBLlRBVxhbhGtBLtRCfxnvhA9BH9JDKpmtRHWiQZSRaSjXRdyakU
Vkoq5ZWqyunKpcqVSmulvfJvVUtVZ9VI1VjVfNVy1XrVDrma3EUeIE+Q9eQZ
soFsJFvINvJZdV/1QLWl2lZDremtmazR1hzVnNSc11zUPNfW17Jr22t/1I7X
amo3ajdrd2sPa09rb2pvKTQKg9JK4VJ4lA6KgNJFEVFkFAVFS9FTZiiLFCPF
RLFQHBQXxUNtpAqpcqqKOkl1Us+pF9R76gP1D9Vf11TXXMeqa6sbrpPVqeum
6nR1s3XmOkfdcd1T3SuNQWPTuDQerYMmoIloMpqCpqXpaSaameaguWieenZ9
b/14vaZ+o36zfrf+sP60/qb+ls6kN9Gb6Sx6G51PF9NH6Uq6jr5F36Yf0I/p
brqX7qO/NnQ3iBsGG4YaRhuUDe6Gy4bHhpdGYaO8UdXobLxvfGj0M9iMVgaP
0c7oYAgYIoaCscgwMfYYLoaHcc1sYjYzWUwOs43JZ0qZSqaZuca0MreYR0wv
09fU3MRqamsabtI1zTaZm7aatpsOmo6bvE2v3+a+LXxb/XbXzGpuax5t1jXP
Npubt5q3mw+aj5u9za+sNhaXNcySsdQsHWuWZWZtsQ5YR6xjlpf12tLZMtIy
1jLfstyy3rLD5rFFbAVbw9ayd9mH7BO2i+1h37Bv2c+tvNaOVkFrX6uidbF1
r9XVes3hc4QcCUfKkXOUHBVnibPCWeNYOXbOFsfJ8XH8bcNt6rapNl3bbJu5
7aDtuM3b9srlcQVcEXeYK+MquGqulqvjmrhmroN7xHVxPdxnXgdPwBPxZDwF
T8vT80w8M8/Bc/E8vOf2jvbv7T/a99pvOwQdfR2KjsWOvQ5Xh6fjmi/mS/iD
fClfyZ/mL/FX+Gt8K9/O3+K7+V6+r3Okc6xzvnO9c6dzv/NN0CUQCWQChUAv
mBEsCowCk8AicAj2BC6BRygRSoVyoUq4IlwTWoV2oVN4L3wQ+oT+Ln3XTJeh
y9hl6rJ02boc3eLuwe6h7tFuZbe7+7L7sfvl+4/vez29Pf09kz2anl89Jz3n
PRe9/b2TvZrew96T3vPei95nkUykEGlFJpFZdCJyiTyiZ/GgeEgsFY+KleIt
sVt8KX4Ue8UvfYt9tr5riVQil6gk05IlyYpkTWKV2CVOyV+Jr/9X/3n/Rf+f
gYkB28DZ4NCgcnB60D14Ofg4+DI0PbQ05B66HPo79CJVSlXSaemSdEW6JrVK
7dItqVvq+7H343ZYNqwenhrWDeuHZ4dNw+Zhx/Dx8NPI2MjyyPrIzuj26MGo
e/Ry9HHUO/pvbH5sfWxnbF+mkKllWplOppeZZGaZQ3Ykc8k8sudxzfiv8Y3x
zfHd8cPx0/Gb8dsJ44RlwjZxJlfJrXK73Cm/lz/I/QqtwqQwKxwKl8KjeFZO
K9eUVuWW0q28VHqVPtWKak1lVdlVTtW96kHlU/nVU2qdWq+eUc+qTWqz2qF+
mtRMnkyeT15MPms2NJuaXc2h5kRzqvFobjS3Wp3WpDVrj7QnWpfWo32e0k3p
p2anHFNXU0+6WZ1Z59Ad6Y51Xt2rfkZv0Bv1Jr1F79A/TS9Nr0xbp+3Tf6df
ZuZmDDPGGdOMZcY245g9mD2efZp9nTPMrc7dGYyGVYPFYDM4DGeGu/n1+Z35
/fmr+befv39u//y3sLqwv3C3aFvcW3QtXi+tLFmX7Et/f23+Ovx1arQYbUaH
8Wx5x2Q2OUwuk8d8ZD42P69YV+wrf1evVu9Wn9asa/a1rbWjNe+ab33HYrOc
We3WLavT6rP6f2///rexubG7cbhxunGzcbu5u3m4ebp5s3lrd9rv7Q/2v3af
3b91tOXe8m75tg+2j7cft73b/7ZfHU+7h7unuze7t3uuvev9q/23g+MD78Hr
4enhzeHtkffo+ch37D1+dd47H5z+k/OTi5Pn05vTW5fn/OL8z8Uf96X70e11
v1w+Xr5cPV29eW49zze39w/3/ge/1+d9fXr7H9QpLT0=
"]], 0.045176762611313204`]},
{Hue[0.63, 0.26, 0.89], EdgeForm[{Hue[0.63, 0.7, 0.33], Opacity[
0.95]}], SphereBox[1, 0.045176762611313204`], SphereBox[2, 0.045176762611313204`], SphereBox[3, 0.045176762611313204`], SphereBox[4, 0.045176762611313204`], SphereBox[5, 0.045176762611313204`], SphereBox[6, 0.045176762611313204`], SphereBox[7, 0.045176762611313204`], SphereBox[8, 0.045176762611313204`], SphereBox[9, 0.045176762611313204`], SphereBox[10, 0.045176762611313204`], SphereBox[11, 0.045176762611313204`], SphereBox[12, 0.045176762611313204`], SphereBox[13, 0.045176762611313204`], SphereBox[14, 0.045176762611313204`], SphereBox[15, 0.045176762611313204`], SphereBox[16, 0.045176762611313204`], SphereBox[17, 0.045176762611313204`], SphereBox[18, 0.045176762611313204`], SphereBox[19, 0.045176762611313204`], SphereBox[20, 0.045176762611313204`], SphereBox[21, 0.045176762611313204`], SphereBox[22, 0.045176762611313204`], SphereBox[23, 0.045176762611313204`], SphereBox[24, 0.045176762611313204`], SphereBox[25, 0.045176762611313204`], SphereBox[26, 0.045176762611313204`], SphereBox[27, 0.045176762611313204`], SphereBox[28, 0.045176762611313204`], SphereBox[29, 0.045176762611313204`], SphereBox[30, 0.045176762611313204`], SphereBox[31, 0.045176762611313204`], SphereBox[32, 0.045176762611313204`], SphereBox[33, 0.045176762611313204`], SphereBox[34, 0.045176762611313204`], SphereBox[35, 0.045176762611313204`], SphereBox[36, 0.045176762611313204`], SphereBox[37, 0.045176762611313204`], SphereBox[38, 0.045176762611313204`], SphereBox[39, 0.045176762611313204`], SphereBox[40, 0.045176762611313204`], SphereBox[41, 0.045176762611313204`], SphereBox[42, 0.045176762611313204`], SphereBox[43, 0.045176762611313204`], SphereBox[44, 0.045176762611313204`], SphereBox[45, 0.045176762611313204`], SphereBox[46, 0.045176762611313204`], SphereBox[47, 0.045176762611313204`], SphereBox[48, 0.045176762611313204`], SphereBox[49, 0.045176762611313204`], SphereBox[50, 0.045176762611313204`], SphereBox[51, 0.045176762611313204`], SphereBox[52, 0.045176762611313204`], SphereBox[53, 0.045176762611313204`], SphereBox[54, 0.045176762611313204`], SphereBox[55, 0.045176762611313204`], SphereBox[56, 0.045176762611313204`], SphereBox[57, 0.045176762611313204`], SphereBox[58, 0.045176762611313204`], SphereBox[59, 0.045176762611313204`], SphereBox[60, 0.045176762611313204`], SphereBox[61, 0.045176762611313204`], SphereBox[62, 0.045176762611313204`], SphereBox[63, 0.045176762611313204`], SphereBox[64, 0.045176762611313204`], SphereBox[65, 0.045176762611313204`], SphereBox[66, 0.045176762611313204`], SphereBox[67, 0.045176762611313204`], SphereBox[68, 0.045176762611313204`], SphereBox[69, 0.045176762611313204`], SphereBox[70, 0.045176762611313204`], SphereBox[71, 0.045176762611313204`], SphereBox[72, 0.045176762611313204`], SphereBox[73, 0.045176762611313204`], SphereBox[74, 0.045176762611313204`], SphereBox[75, 0.045176762611313204`], SphereBox[76, 0.045176762611313204`], SphereBox[77, 0.045176762611313204`], SphereBox[78, 0.045176762611313204`], SphereBox[79, 0.045176762611313204`], SphereBox[80, 0.045176762611313204`], SphereBox[81, 0.045176762611313204`], SphereBox[82, 0.045176762611313204`], SphereBox[83, 0.045176762611313204`], SphereBox[84, 0.045176762611313204`], SphereBox[85, 0.045176762611313204`], SphereBox[86, 0.045176762611313204`], SphereBox[87, 0.045176762611313204`], SphereBox[88, 0.045176762611313204`], SphereBox[89, 0.045176762611313204`], SphereBox[90, 0.045176762611313204`], SphereBox[91, 0.045176762611313204`], SphereBox[92, 0.045176762611313204`], SphereBox[93, 0.045176762611313204`], SphereBox[94, 0.045176762611313204`], SphereBox[95, 0.045176762611313204`], SphereBox[96, 0.045176762611313204`], SphereBox[97, 0.045176762611313204`], SphereBox[98, 0.045176762611313204`], SphereBox[99, 0.045176762611313204`], SphereBox[100, 0.045176762611313204`], SphereBox[101, 0.045176762611313204`], SphereBox[102, 0.045176762611313204`], SphereBox[103, 0.045176762611313204`], SphereBox[104, 0.045176762611313204`], SphereBox[105, 0.045176762611313204`], SphereBox[106, 0.045176762611313204`], SphereBox[107, 0.045176762611313204`], SphereBox[108, 0.045176762611313204`], SphereBox[109, 0.045176762611313204`], SphereBox[110, 0.045176762611313204`], SphereBox[111, 0.045176762611313204`], SphereBox[112, 0.045176762611313204`], SphereBox[113, 0.045176762611313204`], SphereBox[114, 0.045176762611313204`], SphereBox[115, 0.045176762611313204`], SphereBox[116, 0.045176762611313204`], SphereBox[117, 0.045176762611313204`], SphereBox[118, 0.045176762611313204`], SphereBox[119, 0.045176762611313204`], SphereBox[120, 0.045176762611313204`], SphereBox[121, 0.045176762611313204`], SphereBox[122, 0.045176762611313204`], SphereBox[123, 0.045176762611313204`], SphereBox[124, 0.045176762611313204`], SphereBox[125, 0.045176762611313204`], SphereBox[126, 0.045176762611313204`], SphereBox[127, 0.045176762611313204`], SphereBox[128, 0.045176762611313204`], SphereBox[129, 0.045176762611313204`], SphereBox[130, 0.045176762611313204`], SphereBox[131, 0.045176762611313204`], SphereBox[132, 0.045176762611313204`], SphereBox[133, 0.045176762611313204`], SphereBox[134, 0.045176762611313204`], SphereBox[135, 0.045176762611313204`], SphereBox[136, 0.045176762611313204`], SphereBox[137, 0.045176762611313204`], SphereBox[138, 0.045176762611313204`], SphereBox[139, 0.045176762611313204`], SphereBox[140, 0.045176762611313204`], SphereBox[141, 0.045176762611313204`], SphereBox[142, 0.045176762611313204`], SphereBox[143, 0.045176762611313204`], SphereBox[144, 0.045176762611313204`], SphereBox[145, 0.045176762611313204`], SphereBox[146, 0.045176762611313204`], SphereBox[147, 0.045176762611313204`], SphereBox[148, 0.045176762611313204`], SphereBox[149, 0.045176762611313204`], SphereBox[150, 0.045176762611313204`], SphereBox[151, 0.045176762611313204`], SphereBox[152, 0.045176762611313204`], SphereBox[153, 0.045176762611313204`], SphereBox[154, 0.045176762611313204`], SphereBox[155, 0.045176762611313204`], SphereBox[156, 0.045176762611313204`], SphereBox[157, 0.045176762611313204`], SphereBox[158, 0.045176762611313204`], SphereBox[159, 0.045176762611313204`], SphereBox[160, 0.045176762611313204`], SphereBox[161, 0.045176762611313204`], SphereBox[162, 0.045176762611313204`], SphereBox[163, 0.045176762611313204`], SphereBox[164, 0.045176762611313204`], SphereBox[165, 0.045176762611313204`], SphereBox[166, 0.045176762611313204`], SphereBox[167, 0.045176762611313204`], SphereBox[168, 0.045176762611313204`], SphereBox[169, 0.045176762611313204`], SphereBox[170, 0.045176762611313204`], SphereBox[171, 0.045176762611313204`], SphereBox[172, 0.045176762611313204`], SphereBox[173, 0.045176762611313204`], SphereBox[174, 0.045176762611313204`], SphereBox[175, 0.045176762611313204`], SphereBox[176, 0.045176762611313204`], SphereBox[177, 0.045176762611313204`], SphereBox[178, 0.045176762611313204`], SphereBox[179, 0.045176762611313204`], SphereBox[180, 0.045176762611313204`], SphereBox[181, 0.045176762611313204`], SphereBox[182, 0.045176762611313204`], SphereBox[183, 0.045176762611313204`], SphereBox[184, 0.045176762611313204`], SphereBox[185, 0.045176762611313204`], SphereBox[186, 0.045176762611313204`], SphereBox[187, 0.045176762611313204`], SphereBox[188, 0.045176762611313204`], SphereBox[189, 0.045176762611313204`], SphereBox[190, 0.045176762611313204`], SphereBox[191, 0.045176762611313204`], SphereBox[192, 0.045176762611313204`], SphereBox[193, 0.045176762611313204`], SphereBox[194, 0.045176762611313204`], SphereBox[195, 0.045176762611313204`], SphereBox[196, 0.045176762611313204`], SphereBox[197, 0.045176762611313204`], SphereBox[198, 0.045176762611313204`], SphereBox[199, 0.045176762611313204`], SphereBox[200, 0.045176762611313204`]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
Boxed->False,
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
ImageSize->{384.9535460577531, 375.},
Lighting->{{"Directional",
GrayLevel[0.7],
ImageScaled[{1, 1, 0}]}, {"Point",
GrayLevel[0.9],
ImageScaled[{0, 0, 0}], {0, 0, 0.07}}},
ViewPoint->{0.944451038322406, -1.7391349078250222`, 2.744708000607019},
ViewVertical->{-0.2574628756358374, 0.1876871719619685, 0.9478852215064035}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/521f5c2ddef05179.png)
|
| In[24]:= |
|
| Out[24]= |
|
Show the geodesic balls with radii up to 3 as a highlighted graph:
| In[25]:= |
![ResourceFunction[
"WolframRicciCurvatureScalar"][saddleGraph, 2, \
{-0.11849417602213196`, -0.29735987618366094`, \
-0.07273251971244428`}, 3, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/76969908029e47ad.png)
|
| Out[25]= |
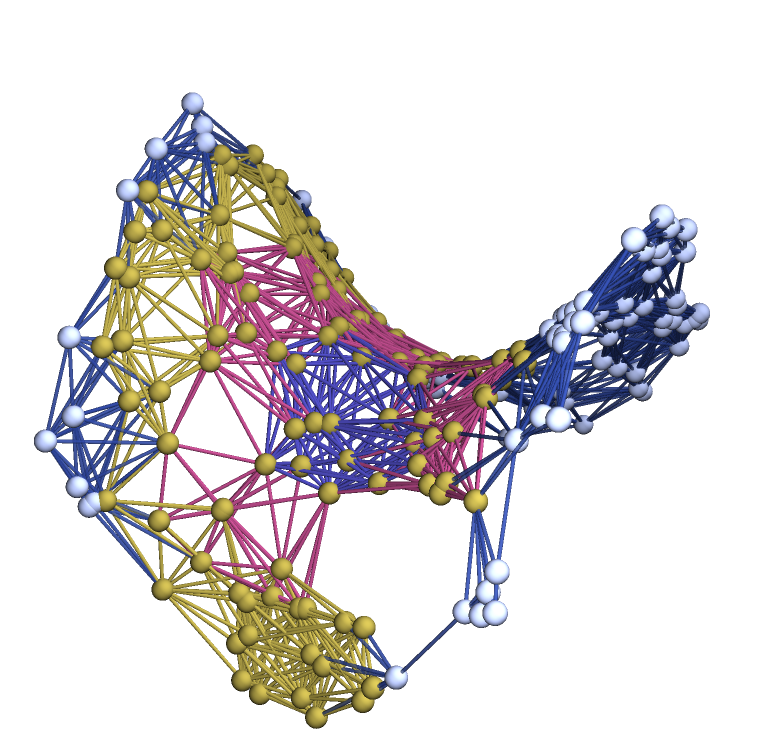
|
If given a graph and a number of dimensions, WolframRicciCurvatureScalar returns an Association showing the Wolfram–Ricci scalar curvatures at each vertex, using the graph radius as the maximum geodesic ball radius:
| In[26]:= |
|
| Out[26]= |

|
| In[27]:= |
|
| Out[27]= |

|
Use geodesic ball radii between 3 and 5 instead:
| In[28]:= |
|
| Out[28]= |

|
If given a graph, a number of dimensions, a vertex and a maximum radius, WolframRicciCurvatureScalar returns the Wolfram–Ricci scalar curvature at that vertex:
| In[29]:= |
|
| Out[29]= |
|
WolframRicciCurvatureScalar also supports directed graphs:
| In[30]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAYA7mmYAq3T8IxMSUWUrvP5TMvnnQ
Lu4/LPamrnjK7j9QXnoCq1nTPzg1VJeN3t0/gKRhpA6Prz+MxpBJZq7YP6jd
7/Z4gts/NlJMenjr6D8g1/Po3OCoP0D+PCTDGuQ/FFsxworK0T+wlLzYgBi3
P4zmzJ7/DOw/kJ1Jc3Huuz9gxKG6LALRP3RBVtc/Ze0/CEUth86/xT8AmE9j
+X25P9iRiKm5F94/0CMkyq3O2T90KAweOhfvP1wVFVHLJ9Q/6BGcj40ZwD94
UfWCtWzRP0JdY8FIYuM/GsVMrRV/5T9os9Hh/gbPP8CLTPixed8/mOCTVqED
4j/EeX89A5PhP6gzJK2w0t4//qPE3b2d5D+4SkeOJ7naP2bh/wlxi+Y/vJjb
NDrD7j/UanOC/evsP+CtTggX2+s/aPfhhZE25D/MNKin
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 3, 5, 6, 7, 10, 11, 11, 11, 14, 14, 16, 17, 19, 20,
21, 23, 25, 28, 30, 31}, {{5}, {12}, {14}, {16}, {19}, {
13}, {13}, {4}, {17}, {18}, {4}, {6}, {17}, {18}, {7}, {
10}, {8}, {7}, {10}, {16}, {13}, {8}, {11}, {13}, {16}, {
3}, {15}, {16}, {11}, {20}, {12}}}, Pattern}], Null}, {
EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx1lg9YTOkex2em+adppj9T4ZLIpa2UFpVcvK9N6Fnh6Q+yl6ehWhtLLN0N
Udom8l9ZlM2VNnFx++OixHtWi8rfohRl8y+SmD/NaKZpus055z3z7Dz290zP
22fO+877nt/3+z3PGbV8bVgsh8VivR74M41/LkdI/0NQgx3NCkB/T7MQfp7t
/uJ7BbLYiLDgv1iPC69nzkF8/lwMsz5/TsvftTwnc15gsZ74PDPrabazYKEF
W+7P9Bf9eT7zOxbz8bks+8T0F0rflH1xZX4VOrwx61LKHSkcfHUhjN3bgGxb
ivYK90hhhE9v6u3m52jlRJh+eIYUjvju2Npy0Tt0fHNUrvc7B5iYkTFp63kl
unih+0Gt3AG27PMIqG3XovPP7MeuHewAfw+9gIjzBiTXFef87Zg9/LlN+sY3
jU1M49X73HW0hyLNjJJGLZd4xN74Qp5qBzn5nuGqozxiiS1HGiKzg9YFZzNa
PfjElcmt70dOsYNuvbfmHSnkE7pkfoLExg6GnNpS5GYnIEZd6508+rwtTC2q
zd4SJyCEl+WvIvxtYY2xRFp4WkAUdpx7UVIsgSPPTBhzvFlAGMLWTZziIoE7
zsyt+VYrIKy7HzR2bRYz/Z9Ilgj2kyUg6tyT692TrZnr64ffWjf81iDIpllq
b6pBzPVi3jcDH7OeC/QF8/UFAoY/fjAVn+G9LycPfMzs07Tdu2k7j+FJ5Hms
4MFIJ9DcIyCWPfQcMyKFA+ctjDTEvBQQubXJlZp6NhzPIQJOIgGhGDJOV+7F
hn5RkcqsPQJi8TW/p/GZLLjiGyePgFABcXaj3w27Z/3gspD1x24jn6gffnHE
mDIjmCRzkh46wSfc1nddd8juAw0xkTfm+/OJ3I1PS5pTDCBPSmgqK3nEdPeU
zqSkXsC/H3oipplLSPJyv6op1YEtAfd5znwuoVuTJxpn0wP65s4cXfeVFdF7
dMes/HQtyLQ9pzu0j0NIXZeovVw1wG3boJ0x79lEsNHBoaZJDapzo+qmRrGJ
/QFl+UmlKpAU+0v9iEYWoaqd8uu0s0oQ0PJot/UKFvH95dNDnW6a83v62/cv
NPeljP8XF9hMbc0xs83FaNHFaDNXHXu7IGWUmbeSCxwYBh1Z0zuyzMydf6k9
I9jMd3ZKeENU9gznHDWVmd+Zlk83cyApMJNDVuYOU5mZlNvbzJRfbBlWkH6R
MEz5xcyUX8QM371jKhuGyfYMM7NedmCCYoOI4Z9M2zdZM0zdr5k33/RZ1l85
iGHq/sxMTq81P3/O+rpPcYwWwlN5Jbseg34Ufr/pRudxW7jctO0qIyqZM/TH
Cj9bSJ27Dw1Z/Zvz6t8k0OaH/CC23IDSA+tOsIIkkDpnLzIUmxaIIdmW+Xq0
td4USDE0qezqrEP8vDV3bXfZwC9N21Z/QkekLta+r0Qwjiwtwnk+SS7vRjjP
ZBv3qhHO82g3U6kQzrNMZDKOAuE8U774gHCeK6+YqhPhPFM6v0U4z6TtRO0I
55k6x0tEynOHC8n2rG1DcaQ+XHjPdld26qmniLpvKziY7EsjovThQFPXwLh6
ROnDgUWksLfRJlIfNsw2ydJRhSh92LCto3GgdeWI0ocFjZ4m5xYhSh8W/A+t
E9YH64j16aB1xvpgH2B9sE+wPmm0j7A+2GdYn5W0D7E+2KdYn+njwgamiiHW
59HERKX+jRhiffbRvsf6rPpHTssimQRifeJpxvrgnGB9Gunfw/pAej+sDz4P
1gfnBuuD7wfrg3OD9cH9wPrgfmF9cG6wPrjfWB+cG6wPzhOdI+Z5R+eIYTpH
DNM5YpjOkZmpHJnnUzlimM4Rw3SOQHXHbpfNg9cjF79jkq08Dc0HUfU9p0xV
hRqwM6anxi8pGHhfeNhUJVfR10vRp+WP9MqVShDiPW5Z8cxKtHnpUMUWmYKe
/zt6HjxzXU3bB6C/AdK7y26jC3GtRWFeXfT6erTKxSg/lN8Jni+Kq7v0uhEJ
4wtFB2e9A1Gjrf7rrH6JwtZsLdrAbwcApO7SVHciWTSYkj7sBXiAnMHUTUoU
k1KfmiFqBdNUaVX3K7qRfFjPj9GZjeCtvzDcr/ATGn/wY9Shsgegfs/JrtVT
9aiiel3IXMkt0KONzEpMNqDAOQtiv3asBMvWu84M+86IvJ4Irz2NPw1wfiLI
/AgYPUvJ/AiY/FA55jN+kJP54TN+6SPzw7PID4/xm5DMD5fJz1EyP1aMX/H7
QWfFgrGKVWI4JmfO6j9SOFC+JmFdUKsYlr/ubtI3sOG/33idvzlSAlVOk5PS
J7DhxLFpLUn+EnjP0yF0288sGOSZaPjnCAmc9/e0iLdsFqxXcyUJTWL4guvs
mtphBE+2j7cvixHDhMxwg+2zPiB7rOGNrbKBs5uvweTnBrBCueh9tVoEqbEX
VLC31a2WWkNq1IM5Gdxgj4VCSI09QLT97SzjFT6kRi3gqDwfd87kQWrUAN/H
tzVKhRWkRjXI/vJ2vh3BgdSoAt5sj2ezS9mQGpXAEPz61OFbLEiNCnBw9sL2
d4H9qGa01w+aYwIo8bux5Hq4Ee3IWe793EMA11fPXSoP7UOBMYU+VYV8WMnu
6vJ3N6BnKdrEXCkfdrX9avOoTY8SFWH8+AQeFMT9q3zpJh3ill1p8bnKhcID
su6H6k/op2pffYfOCqpkMVf9Q7VI51u6LHesFbzetM1RLu9GsvfAOiiIAyP8
IzdGZ6nRhGAH9yzEhkemNTQ3VKrQx1k787R+bLj/Q/+Mdo4KHVEWJHxfyIKB
IQ3nDsQqkWdw7C+f7FjwUGikS9MrBVqQlh3i2WkEBb3b9penKJDbvVPi3UV9
IDY8UuAfqEDV8dwMxyUG8CSiITVUokCzo878r6of512BqPcVHcOkfQN6GFZX
ucW2dWgBm2aB6fFarGGuC0g/djOs2b200pikZpi0b7KKYXJ6tpLhxbJ5G74g
FOD/jiRXzA==
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 5}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 12}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 14}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{2, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 16}], 0.043048128342245986`], ArrowBox[{2, 19}, 0.043048128342245986`], ArrowBox[{3, 13}, 0.043048128342245986`], ArrowBox[{4, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{5, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 4}], 0.043048128342245986`], ArrowBox[{5, 17}, 0.043048128342245986`], ArrowBox[{5, 18}, 0.043048128342245986`], ArrowBox[{6, 4}, 0.043048128342245986`], ArrowBox[{9, 6}, 0.043048128342245986`], ArrowBox[{9, 17}, 0.043048128342245986`], ArrowBox[{9, 18}, 0.043048128342245986`], ArrowBox[{11, 7}, 0.043048128342245986`], ArrowBox[{11, 10}, 0.043048128342245986`], ArrowBox[{12, 8}, 0.043048128342245986`], ArrowBox[{13, 7}, 0.043048128342245986`], ArrowBox[{13, 10}, 0.043048128342245986`], ArrowBox[{14, 16}, 0.043048128342245986`], ArrowBox[{15, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{16, 152, 153, 154, 155, 156, 157,
158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 8}], 0.043048128342245986`], ArrowBox[{16, 11}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{17, 178, 179, 180, 181, 182, 183,
184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 13}], 0.043048128342245986`], ArrowBox[{17, 16}, 0.043048128342245986`], ArrowBox[{18, 3}, 0.043048128342245986`], ArrowBox[{18, 15}, 0.043048128342245986`], ArrowBox[{18, 16}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{19, 204, 205, 206, 207, 208, 209,
210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 11}], 0.043048128342245986`], ArrowBox[{19, 20}, 0.043048128342245986`], ArrowBox[{20, 12}, 0.043048128342245986`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.043048128342245986], DiskBox[2, 0.043048128342245986], DiskBox[3, 0.043048128342245986], DiskBox[4, 0.043048128342245986], DiskBox[5, 0.043048128342245986], DiskBox[6, 0.043048128342245986], DiskBox[7, 0.043048128342245986], DiskBox[8, 0.043048128342245986], DiskBox[9, 0.043048128342245986], DiskBox[10, 0.043048128342245986], DiskBox[11, 0.043048128342245986], DiskBox[12, 0.043048128342245986], DiskBox[13, 0.043048128342245986], DiskBox[14, 0.043048128342245986], DiskBox[15, 0.043048128342245986], DiskBox[16, 0.043048128342245986], DiskBox[17, 0.043048128342245986], DiskBox[18, 0.043048128342245986], DiskBox[19, 0.043048128342245986], DiskBox[20, 0.043048128342245986]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{204.88671875, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/4df7f47da5eb68e4.png)
|
| In[31]:= |
|
| Out[31]= |
|
In the directed case, the Wolfram–Ricci scalar curvature is computed using volumes of geodesic cones, as opposed to geodesic balls:
| In[32]:= |
|
| Out[32]= |
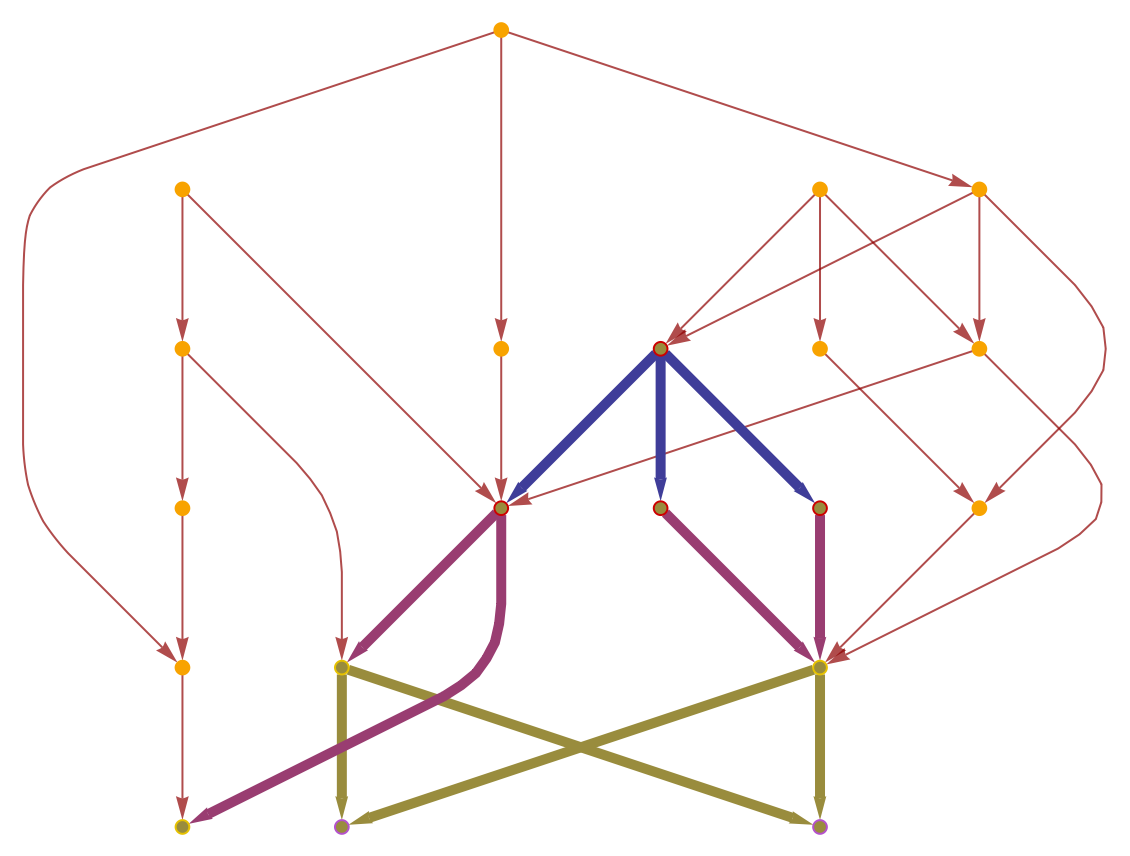
|
However, WolframRicciCurvatureScalar can be made to treat directed graphs as though they were undirected (and hence revert to using geodesic balls) with the option "UndirectedGraph":
| In[33]:= |
|
| Out[33]= |
|
| In[34]:= |
![ResourceFunction[
"WolframRicciCurvatureScalar"][directedGraph, 2, \
{0.41755093473799887`, 0.7045216746619587`}, 3, "HighlightedGraph", "UndirectedGraph" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/77b2f26144583f1a.png)
|
| Out[34]= |
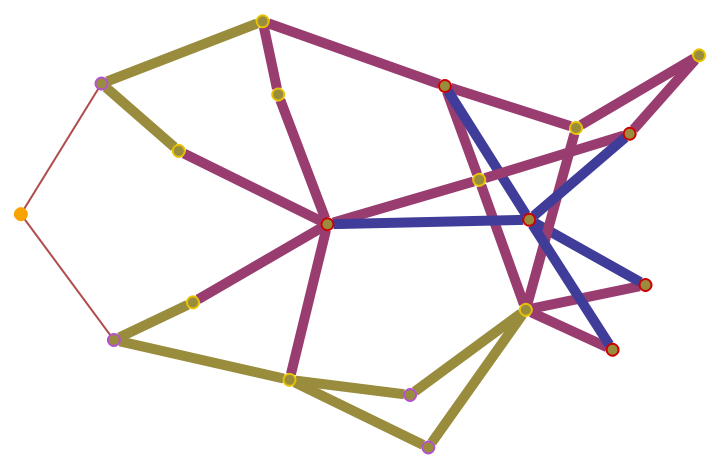
|
WolframRicciCurvatureScalar also supports curvature computations in graphs with non-integer dimensionality, such as this Sierpinski sieve graph:
| In[35]:= |
|
| Out[35]= |
|
| In[36]:= |
|
| Out[36]= |
|
| In[37]:= |
|
| Out[37]= |
|
Compute the average Wolfram–Ricci scalar curvature over geodesic balls around vertex 150 with radii between 3 and 9 in a 20-by-20 2-dimensional grid graph with the option value "CurvatureMethod"→Mean (default):
| In[38]:= |
|
| Out[38]= |

|
| In[39]:= |
|
| Out[39]= |
|
Return a list of all curvatures over geodesic balls with radii between 3 and 9 instead:
| In[40]:= |
|
| Out[40]= |
|
Compute the maximum and minimum curvatures over geodesic balls with radii between 3 and 9 with the options "CurvatureMethod"→Max and "CurvatureMethod"→Min, respectively:
| In[41]:= |
|
| Out[41]= |
|
| In[42]:= |
|
| Out[42]= |
|
By default, directed graphs are not transitively-reduced:
| In[43]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/78eb8627-bef9-4ebe-9ca3-a872ab50f539"]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/5fb1d16df8124e1e.png)
|
Compute (and visualize) the Wolfram–Ricci curvature scalar, assuming that the graph is not transitively reduced:
| In[44]:= |
|
| Out[44]= |
|
| In[45]:= |
|
| Out[45]= |

|
WolframRicciCurvatureScalar can be made to treat unreduced directed graphs as though they were transitively-reduced with the option "TransitivelyReduce":
| In[46]:= |
|
| Out[46]= |
|
| In[47]:= |
![ResourceFunction[
"WolframRicciCurvatureScalar"][directedGraph, 2, \
{0.41755093473799887`, 0.7045216746619587`}, 3, "HighlightedGraph", "TransitivelyReduce" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/21be86ba801b538b.png)
|
| Out[47]= |
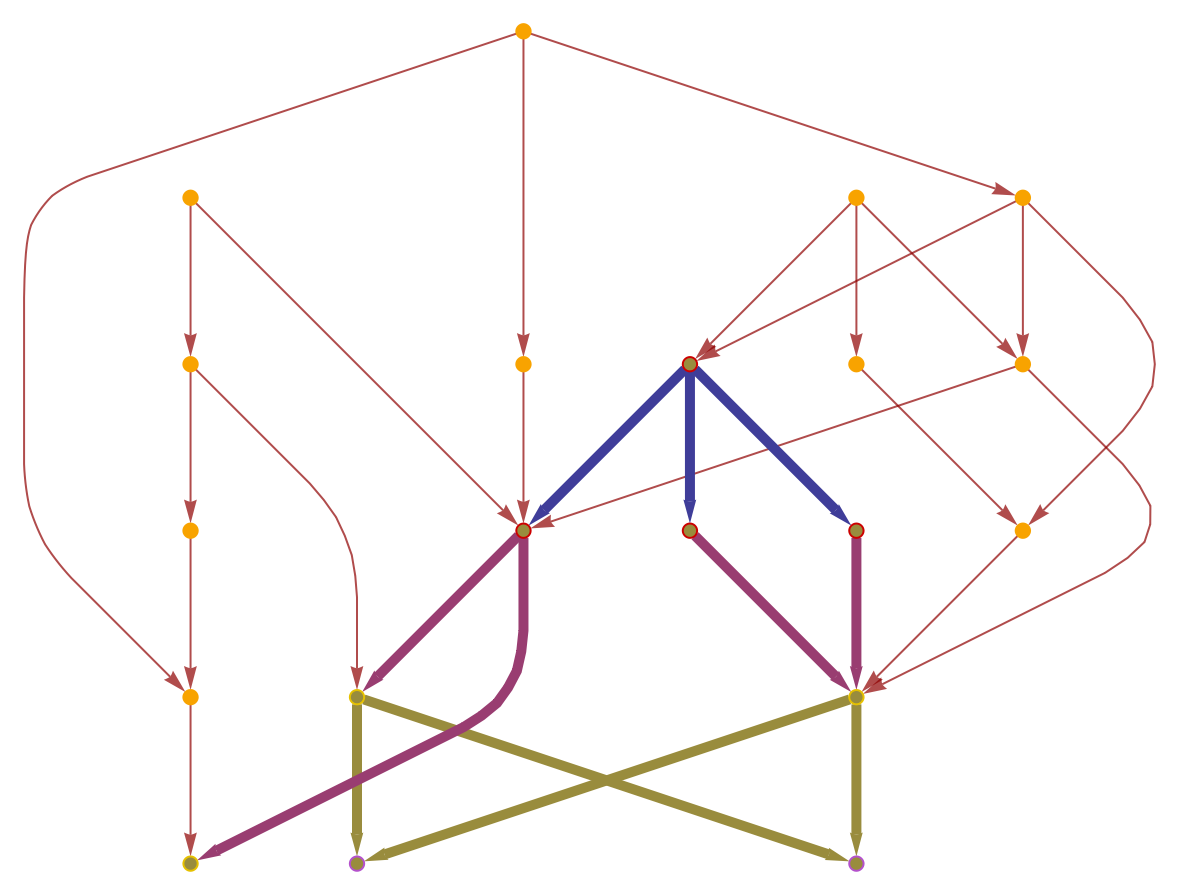
|
By default, directed graphs are treated as directed (and so curvature computations use the volumes of geodesic cones, as opposed to geodesic balls):
| In[48]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAiBDgQC0N7D8Miwlf7rPgP2DD6g69
ErY/vFne0Lkv2D8AYqEgHNmHP0y+xxYqrO0/sBJhl3Rm4T9kbie+Xq3eP6hf
tX6aZ88/ki5iaxFR6D/KvOcIEIXvPyB5b3EiyMs/gEqJn4lg3T8W9qyLs0/s
P7qg/i7vruI/SMlbtu/k0D9I3gFvCW3tP1AaT8UdINs/TnYI2uGX7z/A7Age
bdDiP9B5FJWzMrU/DqNXMXBJ6T+sgi4Z70bmP85zrMZJD+g/cMA/h/uy2T/K
qgmYaj/kP1ycpAlxYeo/MJn6j48Euz9cbg+fJinePwzPqiEI19M/Siz/TIYE
6T/4ia6W8rHLP0BF9wTPFcs/riH/Ot0j7D/kWXJEIx/aP6SzChO3t+U/Pmkf
1Khk6z+AomBv3AKAP+Ys8tyO2+Q/SIuN6pq61D85Ap6m
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 1, 1, 3, 7, 12, 13, 16, 16, 18, 19, 23, 25, 26, 27,
27, 28, 30, 31, 31, 32}, {{9}, {11}, {14}, {8}, {15}, {
16}, {20}, {2}, {8}, {15}, {16}, {20}, {19}, {2}, {9}, {
18}, {6}, {16}, {9}, {2}, {8}, {15}, {19}, {1}, {4}, {
4}, {19}, {14}, {5}, {18}, {13}, {14}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxdmAs0lFsbx2cMc3GZGc2YmZKD41upSUihInvnlm50SEUlHF1IQn2OkCLX
cupDKEpRSaWSOiVHZpcuKIlKnE5FEXIb19zna+Y17yyeNWs96zf79rz73fv/
PDPanvscd8gRCAQVIoEg9lONCTFPRZNfTPJsNLWdMMnUSWZOY9wmWQgwz5tk
9rT5pSYdLxRMXU/aX9oujY89LZ7p8UnXlcaHxyOYtj6aGp+Up8+P27T5pPtD
ncbTn08aj9RL58fjnMb4fsJp8cCp/XnT1pMyPg+a2l+6H+xpzIQiiakjp6q6
p+3nGfjz3LabGVxkLGOe7yOO7yM6ztFLq7MIVjIeyxcPUME5vEb3UI2ujMmZ
fpWM48o4n2ZpKBo2KeG8SGJKeDzV4uGHFPH2wNnPA2Y/p+HMUhWbjPMVtvz8
yN7H+pFLDiOXKDh3d4mNjPOJr0t+fmSsXxe5oC5SAefFknhIsH9+5RnFUXWU
/DhdZ1W0HKy9tXgXv0Md+ccuv5fVQoQXjpvs3v5GHVVFqLebuxKhs6Dm7NV8
dXT99uLHsz4S4MBqmgItSh1RufFmZv4EeET/nwuH1qmjptu8TZksAuz3tvGn
qKijMPnn8+JOiMCG8dX7cx7PQkbMN22bOSKQ2fr9qqvfLNQc49x1s2QCVJGX
nHF15aLLS5JD7OzGQC6RU7Uqjo02EIMDs8gjYH591Jq5Q6pI2ECqfTD8A1yZ
RdPocGKgoPcmlxO1B8Eac77hTjMl9L2J2TA3vB9A7t7XJTkUtJaWFHOY0Qei
rlePD6TIo7PWRadT3vWAWcObCpVocqguNZ6z57X0fBEIVzJvH38PRDh7JhoJ
D+yZwBnbz3GclfdnWxFjxnAe8RAPGJWx+HU5jMj6m39M1+QM47xQdxnbvewH
zjslNgjK2hI0QrmBAg3js/RwhYFJThKUvVI71lvUB4ixFhE+rpcEuxe9qSuN
6Z1sLxD88Hw70rO7B6xaoOeWb10sCN02UxjmIZzs/0TQaGMdUN7QBUaeguj+
Oy8Ed3d+zHWc3zk5vkawR2MiJiW7HTRu2ll9v7lWQPXJUUqy/Q5cdEi3OH1f
BY5+4bkHyN8AABHHB8raBR7uYFm0+hfwWsAB5iE9Aq8jNRGxSh/B8t6jpVVF
/YIY9aFg92O1oNWE6mSc80NgkNTtknLnNaj582Knr/mIoKgsYNVa+nMwNOic
HHRoTLDUbv2ONexi4Baoae3oPSGY/w+15IPPVVxvru7q+DJQxYVSdrkk3lEu
JE6y8j13pXvusvbSs63rj2jL+PBm8QAOzqAt2aItWcbyDve/xdrIuDKersDr
VcM5/YzYZCwZbiHjpZILyMbjiY8Tm0wf68XHZ4GM54rloIaFc/AfYpOxWB0C
ZsuYK9GrGdPiUcX5uyQeGWPxMPF4jknikemz5DgvkDGmLwychRJ9oeOM6YuM
sfuggrNU73IKYCuq6wZ9cWf6X0cpwrMVclmk37vB0IUlI6iZBj+ttOWXZXaB
FaFMa9JGGvTlK0XREzpBBVe7Ju0dFdoF/nazlt8BTgf5XAr3osJAzZlXtUK/
g9y0jqL7clT4faHngY6wVjAackXNKp8C86/qMZcZfgNJWhl3tfZS4KOY4DBa
ylfgG/c8bf1SCnxt+KajzyMOvFw8GsYjk2GqN8Fd3qxRsGtY9MChQx7Osf8t
ft0FoWB57Tv7wXYSvHF55n8y3/8QrH4RZqasQIKeZi6EA1YTglN1/YcTTeXg
RQr1ZEsPEfEmls+OOUqE15nnSzZtlUfvzDYzv7cSYEVhzwlFDzJ6lWi19eEu
AvQtvDpT7ZkQNCWmPAh5xYW9FcsuL8/rAdbrbqcKT3Hh/0zvZB8s6AUaRk5p
Hk5caDMxY0Z5XR/YB0P/rqRxIUvTtW++5gAwD55HMi7kwJEzcbbZ0YMgsn6b
X5obBw75ZSrpKQ8BKy/eeP+YGmRkZliWFwyDQzyXW+uS1aCF7pH2gwdHwcJB
zegsbTWYV37t2HnfMXDm1/jk8s9suOsxfw7fahwEX7R2GE1nw0BVQsnM8XFQ
GexYaOLEhmX3+I5+6RMgNbvgVSiVDX0Lrn3RVReBt1o7kiqKWHCb/JF9todF
IK7Pm6Tjw4IZedeGyp+JQMGsR9rRHBbUvc4PL+gRAcdUn06hQHp+CVB6fjn7
v0S1dorAKpUrR7evUIWuL+NZ2fd/jt8fnV3cxYQVSoPX9baJwIeXiwfzs5jQ
a6GufdynCVDC+yvc3JUJ9ZZrjNw1mwDbN5HNt/OYUMug7lbBgXFwUPW3rUaF
DLiCsnlfRPwYyHMxvfZ2NQOeeHp2iXbIKNgaK/C43EqHmM6NgMj0tshLiXSI
6dwgSMnQ5J+LUIGYzvUCXt1J+8YYZYjpXCegr18m9M9SgpjOfQOBJE3G2mpF
iOlcA7DtXX49kKMIMZ17DxJmpz1p8qdBTOdeAstI/pbsBirEdO4B8NYZ8ru+
gwpn+fnYRi9ko3Kd+fsHzlJgcYG9N2MPG8Wley5onEeBzZV5uzPz2GipV45+
aQ4ZJgqirI0G2ejTkcGgDBYZPo2tHatYqYaChI5kH38FGD4nO3F3lhqSv/P3
v/oP5WFJRoucEomDosoMR9qGSTCqJWd9gS8HDRsWuGXMIcEqWkOI2ycO8ugA
ilZWctBH8r65yMhmhm6ygAjT84/FV6znom7b+MxBY+Lk++ei0z2X/PfmEGDB
jWOnMnK4iG+z49wPJmHyPHDR+qOnVvHbJwCP2JBR/ZmLfn11RSUhdxxg54OL
ynzkY9muY6BCcjy5aKXLtb9KRdL8yUPS/OjEoWrwRrmoRXVRWxZtAGxw0Trg
3vEznhUB/REv+sBYmZ1C/RsuOjyoFUfO6wX2OyJeR9zmomQDy0sG13/mR/2K
d67RXKTf+dZuvEwIunR01LwcuMjBoP6/+xSEwMI24cQ5Bhd1tJ/bqPyoC5ik
KFhSnnGQXaRvTeTdTlDHPGmQFchB+dq/bLds7gBp3oPDhspsJJEZXit41Sva
f75OFWU0i1osbn8F3Zs3mdXfYqCPt28GFWz/DPgL+joN2cpog+u3Dx5z64CD
5xuRzScqOvckR3S8uBq4Df3w59HJKKjxc6nHkjKwodt9Re5FEsoNoShZajwE
JivpAQOZROS5v4m5qfsqwOpLCsLyozRfUJEk3aWzJvWfirD8KGvH8qOMwyUD
ZuCMJTgZY/lRxi8l+VEVZ+l9TnJWA/VDFHTLO2UGA6pC+43OY15fKci+2eJT
SBsTGsgh04sCCjqonDr2bwoTGrs49yT/SUF6n9P3Gtsw4e9b1OaZrqOg2qJ0
T2o3AxZSCZ8TJsjIh77lZJILAy72UGOlZJER80GQB62CDt95OT91MPmpt0Wd
db6QDjNZaKC4WAGdl3gVSK5al+VVL48wrwzDTKsUOGR5hHllOL7WWqfakoQm
JF4JHmPcGE45KYcwrwh/PUyL9+ogIh2Jp8GyDJdqcxciwjwNHtxxruaXWgLC
PBWa/vs2QfF3AsI8FVbbCj9ufEFAa7qO2vErufCovPM960dE1FDiU3PzJBfy
lurHlzfKob8D7p77cyUXJjSFbmzWk0efyB7XnvVz4BeyxS+nsxWQXbj/kEsa
B/IuHGhotKSgkfdfYlcacKBhvua5xyo01M8q3HyyWA3yTcGGZSQlZGIk9FkI
1KC88RuFVToqSGB0vGTB/Z967ml/lvlQBTmaazncOM6GWaS8+8iajvhOTddS
XNkwiduxyaWIjmz+eF/9TYcNUzPph/7RYKDs3OHSCy0sWHCapWu9j4EsW1ZH
lF5mwSaFUefUmww0Z9ELmoMbC+p9e0Kr/sBA9gkh26xUWTBhaYBl/yADPejd
HHahRHp+mGhq/cJEU+sXJppavzDR1PqFiabWL0w0tX5hoqn1CxNNrV+YaGr9
wkSVL8WmjLPkOqnLGKvvlfB4osTL1yni7dj9kHHoM303UTENZ+z5ZCzpXiH7
/yHPUPyDgAr/D/YhGQA=
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 9}, 0.05783410138248847], ArrowBox[{3, 11}, 0.05783410138248847], ArrowBox[BezierCurveBox[{3, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 14}], 0.05783410138248847], ArrowBox[{4, 8}, 0.05783410138248847], ArrowBox[{4, 15}, 0.05783410138248847], ArrowBox[{4, 16}, 0.05783410138248847], ArrowBox[{4, 20}, 0.05783410138248847], ArrowBox[{5, 2}, 0.05783410138248847], ArrowBox[{5, 8}, 0.05783410138248847], ArrowBox[{5, 15}, 0.05783410138248847], ArrowBox[{5, 16}, 0.05783410138248847], ArrowBox[{5, 20}, 0.05783410138248847], ArrowBox[BezierCurveBox[{6, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 19}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 2}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 9}], 0.05783410138248847], ArrowBox[{7, 18}, 0.05783410138248847], ArrowBox[{9, 6}, 0.05783410138248847], ArrowBox[{9, 16}, 0.05783410138248847], ArrowBox[{10, 9}, 0.05783410138248847], ArrowBox[{11, 2}, 0.05783410138248847], ArrowBox[{11, 8}, 0.05783410138248847], ArrowBox[{11, 15}, 0.05783410138248847], ArrowBox[BezierCurveBox[{11, 174, 175, 176, 177, 178, 179,
180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 19}], 0.05783410138248847], ArrowBox[{12, 1}, 0.05783410138248847], ArrowBox[BezierCurveBox[{12, 209, 210, 211, 212, 213, 214,
215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 4}], 0.05783410138248847], ArrowBox[{13, 4}, 0.05783410138248847], ArrowBox[{14, 19}, 0.05783410138248847], ArrowBox[{16, 14}, 0.05783410138248847], ArrowBox[BezierCurveBox[{17, 235, 236, 237, 238, 239, 240,
241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 5}], 0.05783410138248847], ArrowBox[{17, 18}, 0.05783410138248847], ArrowBox[{18, 13}, 0.05783410138248847], ArrowBox[{20, 14}, 0.05783410138248847]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.05783410138248847], DiskBox[2, 0.05783410138248847], DiskBox[3, 0.05783410138248847], DiskBox[4, 0.05783410138248847], DiskBox[5, 0.05783410138248847], DiskBox[6, 0.05783410138248847], DiskBox[7, 0.05783410138248847], DiskBox[8, 0.05783410138248847], DiskBox[9, 0.05783410138248847], DiskBox[10, 0.05783410138248847], DiskBox[11, 0.05783410138248847], DiskBox[12, 0.05783410138248847], DiskBox[13, 0.05783410138248847], DiskBox[14, 0.05783410138248847], DiskBox[15, 0.05783410138248847], DiskBox[16, 0.05783410138248847], DiskBox[17, 0.05783410138248847], DiskBox[18, 0.05783410138248847], DiskBox[19, 0.05783410138248847], DiskBox[20, 0.05783410138248847]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{182.63671875, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/58dc7cb4c954ba6e.png)
|
Compute (and visualize) the Wolfram–Ricci curvature scalar, assuming that the graph is directed:
| In[49]:= |
|
| Out[49]= |
|
| In[50]:= |
|
| Out[50]= |
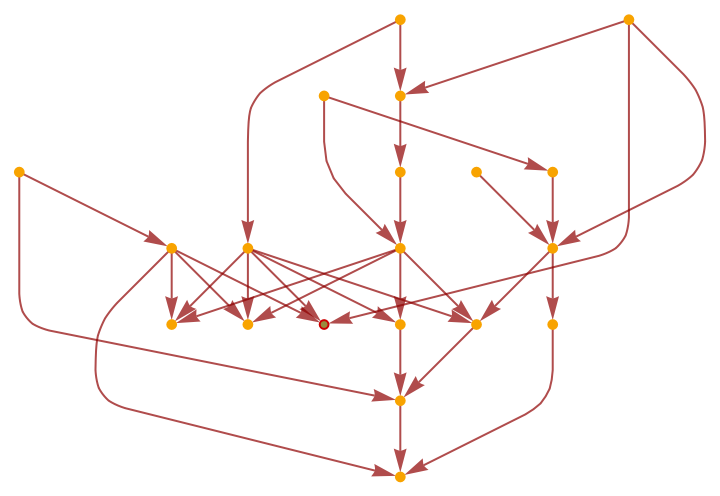
|
WolframRicciCurvatureScalar can be made to treat directed graphs as though they were undirected with the option "UndirectedGraph":
| In[51]:= |
|
| Out[51]= |
|
| In[52]:= |
![ResourceFunction[
"WolframRicciCurvatureScalar"][directedGraph, 2, \
{0.08622342695413243`, 0.3779129543048858`}, 3, "HighlightedGraph", "UndirectedGraph" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/61d/61da70d5-cb3d-4415-92ab-2100010ae567/679c8d31ce5e088f.png)
|
| Out[52]= |
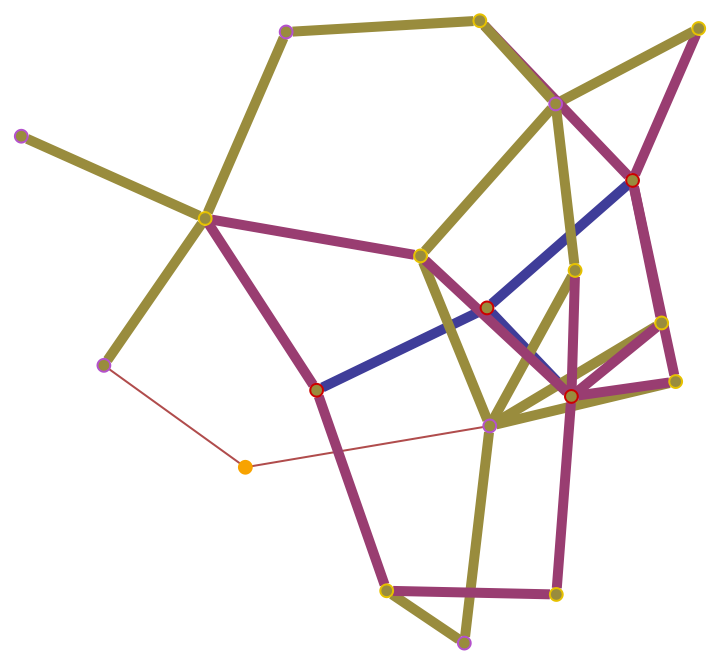
|
Return an Association showing the geodesic ball volumes around each vertex in a 20-by-20 2-dimensional grid graph (default):
| In[53]:= |
|
| Out[53]= |

|
| In[54]:= |
|
| Out[54]= |

|
Compute the average ball volume across all vertices with the option "VertexMethod"→Mean:
| In[55]:= |
|
| Out[55]= |
|
Compute the maximum and minimum ball volumes across all vertices with the options "VertexMethod"→Max and "VertexMethod"→Min, respectively:
| In[56]:= |
|
| Out[56]= |
|
| In[57]:= |
|
| Out[57]= |
|
Return an association showing the Wolfram–Ricci scalar curvature at each vertex in a 20-by-20 2-dimensional grid graph (default):
| In[58]:= |
|
| Out[58]= |

|
| In[59]:= |
|
| Out[59]= |

|
Compute the average curvature across all vertices with the option "AverageVertices":
| In[60]:= |
|
| Out[60]= |
|
Compute the maximum and minimum curvatures across all vertices with the options "MaxVertices" and "MinVertices", respectively:
| In[61]:= |
|
| Out[61]= |
|
| In[62]:= |
|
| Out[62]= |
|
Compute the average volume of geodesic balls around vertex 150 with radii between 3 and 9 in a 20-by-20 2-dimensional grid graph with the option value "VolumeMethod"→Mean (default):
| In[63]:= |
|
| Out[63]= |

|
| In[64]:= |
|
| Out[64]= |
|
Return a list of all volumes of geodesic balls with radii between 3 and 9 instead:
| In[65]:= |
|
| Out[65]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 3 and 9 with the option values "VolumeMethod"→Max and "VolumeMethod"→Min, respectively:
| In[66]:= |
|
| Out[66]= |
|
| In[67]:= |
|
| Out[67]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License