Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the Wolfram–Hausdorff dimension of a graph and its associated properties
ResourceFunction["WolframHausdorffDimension"][graph,v] computes the Wolfram–Hausdorff dimension around vertex v in a graph graph, with an automatically-computed maximum ball radius. | |
ResourceFunction["WolframHausdorffDimension"][graph,v,rad] uses the maximum ball radius rad. | |
ResourceFunction["WolframHausdorffDimension"][graph,v,{radmin,radmax}] uses minimum ball radius radmin and maximum ball radius radmax. | |
ResourceFunction["WolframHausdorffDimension"][graph,dim,All] gives an association showing the Wolfram–Hausdorff dimensions around each vertex in a graph graph, with an automatically-computed maximum ball radius. | |
ResourceFunction["WolframHausdorffDimension"][graph,dim,All,rad] gives an association using maximum ball radius rad. | |
ResourceFunction["WolframHausdorffDimension"][graph,dim,All,{radmin,radmax}] gives an association using the minimum ball radius radmin and maximum ball radius radmax. | |
ResourceFunction["WolframHausdorffDimension"][…,"prop"] gives the property "prop" for the specified Wolfram–Hausdorff dimension computation. |
| "Volume" | the volumes of geodesic balls of various radii around a given vertex |
| "AllVolumes" | an association showing the volumes of geodesic balls of various radii around each vertex |
| "Dimension" | the Wolfram–Hausdorff dimension at a given vertex |
| "AllDimensions" | an association showing the Wolfram–Hausdorff dimension at each vertex |
| "HighlightedGraph" | a highlighted graph depicting how the Wolfram–Hausdorff dimension is computed |
| "TransitivelyReduce" | False | whether to use the transitive reduction of the input graph |
| "UndirectedGraph" | False | whether to use the undirected form of the input graph |
| "VolumeMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls of different volumes (or simply return all values) |
| "DimensionMethod" | Mean | whether to take a maximum, minimum or mean over geodesic balls yielding different dimensions (or simply return all values) |
| "VertexMethod" | Identity | whether to take a maximum, minimum or mean over all vertices in the input graph (or simply return all values) |
Compute the Wolfram–Hausdorff dimension at vertex 150 in a 20-by-20 2-dimensional grid graph:
| In[1]:= |
|
| Out[1]= |

|
| In[2]:= |
|
| Out[2]= |
|
Compute the maximum and minimum curvatures over geodesic balls with radii up to 8:
| In[3]:= |
|
| Out[3]= |
|
| In[4]:= |
|
| Out[4]= |
|
Return a list of all dimensions for geodesic balls with radii up to 8:
| In[5]:= |
|
| Out[5]= |
|
Show the geodesic balls with radii up to 8 as a highlighted graph:
| In[6]:= |
|
| Out[6]= |

|
Return an Association showing the Wolfram–Hausdorff dimension at each vertex:
| In[7]:= |
|
| Out[7]= |

|
Compute the maximum and minimum dimensions across all vertices:
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
Compute the average dimension across all vertices:
| In[10]:= |
|
| Out[10]= |
|
Compute the average volume of geodesic balls around vertex 250 in a 10-by-10-by-10 3-dimensional grid graph:
| In[11]:= |
|
| Out[11]= |

|
| In[12]:= |
|
| Out[12]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 3 and 9:
| In[13]:= |
|
| Out[13]= |
|
| In[14]:= |
|
| Out[14]= |
|
Return a list of volumes of geodesic balls with radii between 3 and 9:
| In[15]:= |
|
| Out[15]= |
|
Show the geodesic balls with radii between 3 and 9 as a highlighted graph:
| In[16]:= |
|
| Out[16]= |

|
Return an Association showing the geodesic ball volumes around each vertex:
| In[17]:= |
|
| Out[17]= |

|
Compute the maximum and minimum ball volumes across all vertices:
| In[18]:= |
|
| Out[18]= |
|
| In[19]:= |
|
| Out[19]= |
|
Compute the average ball volume across all vertices:
| In[20]:= |
|
| Out[20]= |
|
Compute the Wolfram–Hausdorff dimension at an arbitrary vertex in an approximately 3-dimensional graph (produced using the resource function FlatManifoldToGraph):
| In[21]:= |
![graph3D = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwNl2k8FNwXx4cWQrIkSoutQipJltDPo5RKRYska9n+klTK+khZQpsiVLIl
yxMSQshOCA3G2BljMJsZSRLRf17cF/fF/dx7f+ec3/ke+UvXTjvxEwiERt5a
xlulyXWnf8hMYq5S04z1lo0hPpeAKmkOzF7P/wyl1qHlUbxA68oxuMpk0M5U
tUCJtOpt7ewgzF7kO92ZG0KyetPB+cJhyM0ZxqnJ1ELU0J5v0pwNmcAp8bmp
Tsxoi78Tu9CDAUNvbfPHdBS+kdpbvmEI2Xa3gsV0uuH5TClTV5SJzN0x+UPu
RBDm88MeGFBh7ZUzY2fOQWOZ/j+v1L/BUPLpktOLZ0hO5ujmnK+Affkxuvl8
FyyGZ1+s62Ag4FAL1VGSC32VnWO9P7tB/BWbW1fMQCR09Tri2ChPVREgMznw
qbkjKZjVDbEfYr2xve3Y77DmtuKGEVCWvhTy25AQcuFHmJ0/CWHXmdL5pZOg
3BTbGl9AQWHfMP186jjqbgXwZzt3wefjD7jwtUD5JpN0VqIe8ydva4mLciBI
3MGnYN8C+7LtIQ736LDuLCj/mdCPmIM515+Y9oLwWov8TbEdrv3rXG1mOuGj
tynYiNoMsVv/CriFlyFbiC1kE9yLNLZLbf2eIRT+2p30bu8g1Acvrb7XxkYL
94HGqA4N9sSd3X1/v6FKJZssoZuCKZGaJMM1JIRXyBn7NtOxNvXLQlZRJ+KH
O+wUm4dwyXLvGX9jJppH7taLenEhuoesfDJuFCIXxbgCbC4if+xb+o88gen0
/wnJf6Mj6uu6ctmSNvz3OKOm6gcNpOK/kcFm/Th0O/R0Ug0J9v+siGph1ELd
ftng9YwP8FzhlUjuboSnUPyho3ajCGOqXtRSp0IkSSBCXogEz4oDp001ivHw
0RaTcwcpmPmgU3xgGwvWRR/fWyt1gujc9TbDuAiPHxdNm7ixkSd/pzOXzMBU
tcXuQbkxVBm/67CqbAA189jBykPjsL/pHyyimY0o/l5fskoLgtqUNC9PpOOw
lLjDMrURrOwnSHqmcGGyxbt62IeCIMdUwuyu+8h3SfWsThxH0O1FiveJt3Cv
Cvc4otSFRlc+xzMWNZCZtiLKc+phqezG1dkwhj+uiQcsrMi4tLieLGxPR2am
b64nsRHhG3OpDiNkDLh0xyo858C+Qc845msH/EROHA6sZeCs0Imh9ZRJaInw
3XI7wkZJz92XD56PItL0lW5uyBiYCxbCjbx/Bk3mWLr0D2NXyBHxiNMTUBLL
O+MwO44AuRSx6xJDIMg1iLV/VUJJa4rNlYZxTIU6SC+zy4PnoIceLaQcCsOB
nx3kJhHDP21oE92O2485a1WkaVCKiRB9/52BQnHTaIb+IOL3dfQv7OmA5hif
SpYtESJ7hm+lTjFxT8raUWuSjmyWKV8T774pl/VPspmdSLjfe86NM4rZemcT
m04G4qU31oSltOIQXe9kTOYgKo7USFplUhD+e+F8snsP7G+Jmm3R/Qwt5XdR
WXUjcCsyiVw5y8VGJ7csvVdUuIuZqlRYcxAvK1CnFcCCyQKd6f6nEerP6aeK
PTrgs9UiipXchoAPP6ScJQYQFM22Hdv1FHRldz61P0wkf5jxkGZ2oUXVbVGf
QYNIo5+TuDYRPk2NyiHGJOTtm5xPp3KQ75Yea+Q+gVTFadfJS3Rc2sMy3V7E
060k7/SU7QRuBFokXtJnojH8/bGHxV2QaDBadFKgQcIVK81k2TDxyU7tTPoG
Hb4Xd84rU1HSsjhkQaNj5gWReLuBA9eB7853YpgIo923Wfd6DJvtQmId4qkQ
u/f+dvbzBpDZVYPHHNmoCLYNfTPPRvyST0mPxAjify39tqTVgBgeoiDaTgNd
suDySOwkxvmXbDNW0dHzoh7nltpgbf1hjZw5CQEBPQQhKRLkZH+bOVxPg6fn
hfDanEFsFNU7R2qdhGe6nfPuJSZ8bBfFafebMZeeOq0gSMP+7W45T27QICak
HHa4chRm5wJVRqPLUG5UkCPowtPvtmNbmTwbPcJPH3+ub0fu11dHW/jYIHgu
V7ZfokE/6PKNcOt2zN04lLr5Pa/OX1wnlFV/Q/J/Olr6pV/gNZhwdb3QGGI0
Qm+OzFNRF5muQjvPgZjy5+dHSiZhzxmKH64sgn3+aI6eQAUs31Y13hzuQvp+
lXNOpWNgC/TXp3N5flahzTidVYTZBoe+zuxRzNRoHJhJ6wT/tGVfmjAVU3Ye
3tKnhrHhdY3mz6kRaC5d8frB1wuJBYfYaD8OnMWod/w30mAYcn/qZ34uDJ/E
+eiqMKC+6eTDmI8s0L8l+Rl5dUEu6mlR7OYMECStmnpUeXqVnr85f42LhvyN
wbWkMQwcPH7ioEsv7PfH9ZTmdEPkYb/iL5s+lMt9eSe5qw/qraGbZTcUQt32
6rm6HaVYaXBv/Y2bNLQJiaecbeL55GrK3Q2uHRDc8sr6+ws6xOIM9vkWtYOp
KLj60u9JRNq3G2TKjsJIeg/nRfQE/mwoeNda0gmx3Q7h2l/70Jwed66ByETg
sZ9jP7OY0Nh2oeQJnYa8O/QlL79B+Cwv0khZqoZcVdKje9QPqKqeF47uG8eA
drvvuAYLFNF9XpuWl2NmVlz8Ae98ssHUdo8/PB1a/3f6tHYlLFW9hFjKQzDZ
5/JG4M0YPAT/7vMic+DYMCDzSX8A4/8pRpy1m0Sb9qmItVYsZDv33Th8hgu5
BI1C08wm5Jko+f/3cgJa07E1ghdoaKmaLj88yuLFQymtJJgCtRPk20e5VBB/
hhZmVtAx9KZWdH3KOHyqsTtJmgl3EQ/fe3vGkDyimWVzOA3rZBbOr3lKgcmy
3hZ+j2YE3W9rbmLkI3Nkqehv8Cgsi0eMxykclP/SGyZZjkJ0QDVYcTkVLceW
W739QoRb+LKCEL0xJLxJ1XU0YUPoSpTgn6tjIOiZZ4t75sHC+6QJ7SwbGs6f
MmY2U0B/MBzD2UbF4dAdO+1mKSASyHcDdfJwYOHulat+Y+DYtvgLtYxD7qdu
mUxmL/y6LbWceXFTO8UXtaRJhgxObna+9gVqM88yW5+SQbpyfZ7xkYLItYsn
ZOVHoRz4IEf9YT+y3bIXdBJ6YXY/jfV77RjUr7st+i2OwdLrnGU52pC2Z4PU
dkUWvFoZU+oOAyA8uy3gMJYOyl0X7W8DfVDbeVn+ZBYXnkWxCl9e0EB7myhj
VsNC3brCsuf+fRBb7y3nZFsKoR3c5A0XOTweqokVVGjHLvPxRMFWBgzjVY+f
//YCnp8StAtkWaiJa2HzizERNS1s3qvMxsk5Kc3v9xgIX6utcmMXC0HHNIJ/
BD1By9Ps8b1WPfDbs7GEzWCDIpyRksjLd5HWG0IbvEYQtPR4y77JQsQouMp7
tAyBcnH+sjy3H0oTl43XXGPhz9NzBmlONJQvV5mdrCCC+nNr/+uHowho1ckk
qY4iaLxjd+TxZyhhXd75s6IXlqafVl9a0wrC6j0NGbwksSqoz/rXiIZMI4/L
TXk8HlohaSu0vBY+gQzZb0VEeG0R8FIsHEemouPikT9jmLtrVpkk+AU0kQSB
1/5cHmfZKceEUSBk+m7PFVM6Dq8L0eyV5ekucC3okTAHPXG5TibxXSBKjj7b
HfEJQTJBr+ZbOxA5KTfEPsNBlP9WbaveCexSq6E3bx2B+/2XEfWD4zBbJ99j
N9EFteLWJ5RhOsLyA5Q1HrBBeqDjUa1Nh6Zl51cp3j7IbmL/lysNWLezLd6W
MIKN/lv5bc51gfD3VNaYMAXqTWUfmU49kHPwcjhpVoe0LeYs8xAa6lLquPan
yKCNTaQFjo7g2Cpep57i8eb8tvQejxyk2ewK/XV2FHS2Dl9icD8kPmcs51uc
hElUUnWGEY+n4nqkbzGbMXSR73PrNh4PrQskubukwjKlJJEtywSRIdc8kFeE
zWdnKz28eL5QtKxjSDEDRCMvN9MM3nsOn3qoKzqAxuKYata3dhhuX6EvXFAM
jSB5ilwkr78k35F9OtSN/Zv8vC8b0/CyJOy8/qtR1B0WkFoVy0HeHGn5vyer
EZ7zzwa78S6UpBKk3p7mwi+ojEhdy0CmsNH3x0f6MHDfJc59kpfXCjFOfV7N
YB931uXWkmA5Reb7XkSGhlX71KYmJhKH9f2VNSigMAXNVdI64GXuXdrd34HM
OoW91660wJM/qfoRqQtW5QorlL5xcGj2EEkhlwTR23kdwn2jyNMrWGpfxovn
32tHY6iDsDhrfE9uywSCrp+vvbX6LYzWXyEVVNNhH0zw/dryH3YF2Q2bqrJA
CzQUGlikIZms7SmnXIi1jnPBC9P9MCJESOl1jUDtSPrfylou3B9kJiZfHYFo
r9gfQW8u+DkM6d8snk/fkEoM86mFlcke/VxJCkTWJ7TKVtEgWu7Cv7CdBUPd
8pV/j3SCkntjaSC7Ac7qKntkREYhF22dsvrWR8wq/KaUB1BRZUhu864nIZng
/DqW3Ym0x5I/7d0HYGmwsqm1cwDqx3/v6I5uQZtbX955RybSInwl3EM7IfF2
toZjRgMBV0v+iidBZ9WvPy/GaHAezIqS6ZjAzIGzR1P6RqBaNT0fOMNFI11R
TE2HhNtiWx5tmqOCvG5Ljk4pBXIPb2nL62RhY2RTxU3fLlBCg2+tmK5HQP1W
n1Bpno6hwXf+uA3C8vaaNVyZVhh+bvM3X9aOKu7ZRy8pA7CPKLDtE6jBWvLp
jl7BHlgbrORL7uiEToLuvEgSFcnPWEn1x6mw+L0guUqJ91+ZxLecJQ6Mthx+
c9SXhpJ3Ui8rnoyA0PPLpe77UzR8Dc340sHjr2W/r2T96IVImoH4rk90TK0P
Y5mlVUAs4c5Og/mvkMvt9vXemAKzqJaouz94/YTheOqDXDzU3YoPhIxXwtU+
llWhNQKx0pVfKk98grLC8JlIlSrQCu3VXXl6BA1dcRR3eYuECBtja4sRVBEc
w56dGwVlbZPvUd16OJMdXreVjKDOyvSDqm8PCCbmHSffZ2Np3ZMCVuAkzLQe
Xbt7rAP2i/2h//RmILnAa/RLwhtoXYsL+qdrAun1XhENp0ZQIpv8JkduHOEr
VxCUShog5qmnNq73lccPZ9UHPxfiT+mhYkMHEoombYpHTvA4wvbobu72PBB/
PIr/vaoE8cqqvr8iutCTeKjsTXUtNj615nqH8bhZbHH1fjUOdkVzmm4cZIP4
WFqTvrkY2TWt0VoiDFRsvLjwyomCqg81J2Qix5Hck9BUncrjoY1ZWdJ81xB0
7UzENjDh+ZdiE9Q6iKmniRdfbmpCoq6ByMEIKthkYopV6SgssvWEKz0pGFdp
e/dxOxOGQ+K5FdWdIDQvN49bKIegrpLZLuEBWFAdUwrEWTj0aO+11XQGTCzM
h9YO8fJXvI9eOjgI90rFkLXaXQj3Jz3mpLAgIsp3doX2MEqc1Y5xnjEhp70v
JCqXjsKy2lTN7+1IHxhw5Wrx+MK3z04mrQSF5Wns96/ZGM96bWu7YRT25Tus
ilZ8htmFpPdPeHxAOh8vHKDeD3oxo2xdUAPC/NQNMrhcyBjrPZ2rGQehOM6o
qILH35d3VD8X6Ifh78XAAv1uyCzXHXrlMorscx+CTwn3weff02O9HztAEMj1
zpf6DAK7vKy61RwmxGX7yHETaLT0kuDjzSv5hN1sxxU8fmMrRofso+Hh3rAM
4uwADEue8Reu5M21b689dhyoQjJTS3soiQ5X0gLtn5lmMJtjDPZlj8G+6MmD
tWmNKDmhYt39twlVI4XR7Y+j4aPlLKmmNgj7D2k1++4PITNkZGFobx/0j19Z
lJLvRzhN99GpOTKmNPk2fdRtxXTFo3uFcxPQ0ey+yP+DAc+OnF8XtEoQpXPZ
0HmGV5821wfnCP2QyTcbF39Ug+SD1PPK/Mkwe/C/+Kj3n6Av4J5XeZjIm/uP
+hetqgbbwzHNxngcpW9u2n85yoJz0YNTq7UoKBT1s9n9vhN5xncNoryL4Ve9
93LiVgr8Vqtabw5nw1F/jc0l8X6EzLubyWRwEGDIGEhkMxFkOJ8qwYiBXMde
w/odX6Ha6qUjETcGoojeNtb9Npjqfuov302FJY7T3nfV4KzG/atXmX0gqG4W
bXAqhdUrbXpU6SQ4mxga3TwfiQkmzye50vB/RDF5rg==
"], {
Null, CompressedData["
1:eJwVxfk/2g8DAPCtyyxUamq1vq3mGCpyH31TWRgtN1E5om++zmKJ0pzrYE+p
HJ8YNpvWLBEppFBb/BHPH/O8nvcvb7J0rEkKevTo0X/Bjx79/xrv5YM5Bneb
3e5YzQQCg6hCTCC2+rf6vcmtrd6cmuQjhAwjkw3IJrjOgW/Pv3Ob4A6zw+pw
uDOUSmtKToo3rTHtMu3BeY3j4ppwSpwVRyZzyU1kB9mpNWvd2lhaevoDTsPV
KDUaK1nFVakcKqfqOoVEyiHVkNYR9TX19bL6CTifb+VvEbVEM9FNjC1dJr1K
qn3W+sz7/Rd8M2mzdnPTnXUJQoAwoJegKriULOVK+VKpSuqQOqXXxNJ8Zb45
35rvSO7tPUrPzGzPjBGXS5f/XUawMWy2jD1AtKfbM+3tdq3dHsMSsZnYdqwW
u4w1Y+3YmPnmJpZdk12f7X2Wmpqd2pp23ni+dH7+kDbZODm5NHk+eTn5UNhY
eFTo5fdlj9eP94+Pr41vgeFgPrgPrAVvZYxhhzOH24eHb0iRnEhjBLPD3kl9
m/327drrP6/+hiOROCQZyUXykVKkCqlBWpGOtJKSxpLJkvOEpITkhFc4EVn0
WsQVNYlESpFmaHjoZugP7pZ8y71tuhXdYmeJs+2z/87OLjcfjB3sHCTMJ83X
zs9vgoKYYFVwJ/h4MGWwcLBksHGwamRkDrzQt9C/ML6wsIWlZdJo+bQh2jBN
SzPT7LQbWgyrJqrT1aXqXrVaq7arj9QxMBVOJVKpWuom1U2Nvf7x4w9oH7Ff
tT+yP7e/tb8fhCKgGCgbWgOth/ZB+6Ey6AJ0C0fPoNO5dBFdSdfQrXAP0iP1
qDwOj9Pj9niukysLKytbK3srj7I4nCXOZS4ntzl3KaWjsKOjv8PbEeEcNx5P
Hi8dH18eR7AsIiuTRWOx2lnDLDVrlmVm2Vk3rBi2IauB1pDf0KBtMDdYG+wN
Nw0x4mfz589u8i53V7qr2t117l4jARxABuhAPsAFmgARIAWUgArQAFYAcDRb
LOuWA0vk1T9//5PbxemKY8c1x1ni1hNOkk+oJ6UnRydxcpI8Ry63yNflx/JI
1mjuKGe0a3R0afQS9OHlhw87H4IZZ1lnnLOus9GzFDFJnCOuEXeIxXKxVxxJ
O0w/VB/aDw+PDh+giYmYxL5EeaIl8QArIArSBZkClkDQLugVqAWzArvgUBCD
wmBxsEQYAoaBsWEy2A7sABaEhxPCSWFquDY8H94Mu8MnYbgEKyFKqJJSiUAi
UUu0ErPELTmRhCWxJ84n1wlXSVe1V/NXm1dXYdDqy9Wq1Q+rq8HVe0ReXlWe
LG8g7xuSiWOSmUwuk8+UMlXMOSbAdDI9j6cKp0qmBqdweHwGno7PxzfhRXgl
XoO34gH8LTKAC+AD5AA9wA00BUQBZUATAAKB2xfZL96+WANXU6urJdV91drq
BTAPykvkIXgYHq+P18+T8cZ5C7wt3j5UB9PF6RJ1GB1Jx9bJdHKdzqJbTynP
KS8sL28s7ygXlw+We2kfhz7m/mz+2fUTv5GxQd8Y21BuaDY2DtA4NB6dgX6N
pqOb0CK0Eq1B/0AH0LckYY6wXNgoFHYIxUK50CJcFx4LIxllWWVlnLKustGy
M3hUGlVFN6OOqDPqjnqi19FnbSltqW3ZbeVtNW1tXjgDyWAwGXyGlKFiAAwH
w8lwMzyMa0Y0/Xfv7//8RrpwLrKL4WK6uC6pS+UCXA7XrsvpcnlcAVf0CQrF
QDFRUpQK5UDtopwoF8qDukZFQRcvL/Iuqi4GLr5dXAQ5dXWjdZN1S3XHdZfJ
RalF2UVFrUX9ReMZFRXNFWMVGxUHxJ7SntoeSU/Pco+5Z7Pnc4+7J0ZbHFoc
Xlz8uHiz+Ofx06eFTwefTkH1CD1GT9Kz9Tx9jb5eL9OP6yf0Ov2CHhyCh5Ah
aqg6xA/1hbQhawgIgf1wP9XP8Ff7+X6JX+vf9G/53X5/yB9+sZK98nalfmVi
ZWXt9Zs3i28+vvnx5g+UACPEERIJGAKBTZATdAQLYZ2wQzgY+Tr3de3r808j
n+Y+ffr6aT+3hdPS3NLS1TLa8rPlLOnL/Jcvv5A2nA1vo9u4Nr5NadPYrDbb
hg2wBWwhpAKnwCvICrqCq2hSiBRShUKpUCk0CpsCULgUAcXt83fvvr/79e4a
acAZyAaGgWngGvgGqUFhUBk0BoPNABicBpchYLiPMxFMJFOOSWgSm+Qmnclk
Ma2bIinbpO2c7fLtmm3hdse2eNu0ve3djjwuSCtILygoKWgsGCyYLJgqOC94
ePq+8H3l+/dT74+Yd9w7w93dfVFxcX/xePFC8VrxFtQIM8YZMUaCkW2UGQeM
OqPeaFz/6+6vexAEAoMgIBhIHoQNkUEGIBMQI+Qb5AISRPpwPqaP61P4ND6D
b9Vn8/kCvjvf/ZM91N7zvXd7e9/3ruOF8fJ4U7wl/jg+gqUQKRQqpZQioEgo
vRQ1RUuxUw4pR5QTSiytO707s7vb3n3Yfd592f0AmmZOV03zp0emp+em96d9
00HsTOYMa6Z9ZmhmeGbmBnT64XT11Ha6c3rqOw2e3md0lnVWdHI6mztbOju7
Okc7xzrP/gfj0v26
"]}, {EdgeStyle -> {
Directive[
Hue[0.63, 0.7, 0.5],
Opacity[0.7]]}, VertexStyle -> {
Directive[
Hue[0.63, 0.26, 0.89],
EdgeForm[
Directive[
Hue[0.63, 0.7, 0.33],
Opacity[0.95]]]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJw9lnk01usexc1kfL14Z++AXA5OyJjht0mFBkMjDaYockyRDFHRORpJnRMZ
ctWRKURHkqSEMhSiokgDIVORKcN971p33e9az/r+u5/17Gd/Ns8z0NlbSEBA
4Cn//HcnHNw471zxnQja0hOTP7RExLYeX1c1KYpMnVLJzEUeAlIe/73IJKNa
In5UzZuOmFs8ZlX1HNHuJScubs3DyeVma8XgZaKqkZfmNsyCiOXWRK2SBeLM
TY7P1j42kpwS454/miRYE7uYx4YYYAnM1XcncFChTp9ZMOXhyU3dPlPGEMHO
YFhKiClhQjrNZHJ2klgqlQussxKG/Uz0gHQyDS5P78xOmNBRE+tAlySYWC9z
OiLOioxe+p+zYqeWiQrVr5ymZ0y0097/NSvKha6r3/yaKEXcpn1pHL8kgPTu
pcMrrbgg+w68CXWnIbI7qyWgSRlxa9Rd19WxMJyU08TO46BKQ3E4lk7CTdd6
z7zV8hA4FTX+uoOODZv/LhA3ZaLirUbb0sIi4aOx0O9dycHlENIJTc4HYnFA
+UPifTJKBgp/NIW+JGKjfxofNCfjJ3G5VOMIDQcL7p9o7JBG/WDm2iRdGsRV
5n/sPcPGr6P3v9qsYuHxvSnlV7GqWCmwHLMcQoXD/a6TqY4spGiyaKXbZoj4
1O+UehUWBP43hQKOSo1nlNG0WiRn8180+DnZ3LgmR8KeKrGXPhMUmGc8Tv8U
rIbWnLzzIn19xL3PZM2P+6jQ/Sa/071SFPtJFh0GI6rYvPHdaUM3Blbeo0fI
l3NQSmLFUA2UYHiMvc0iRBaZZ/Yam3TzcN+wTdfSnwRuufHbHuchYnulxAtp
KwqGwu0UGvLEYUPTrChuEEFQWHqYnbE87l5iDs+EiSDl/diA2HUyfhFqXYg7
Q4NDfdkYb5KN41SWFjHO1/NiXDdlkoI+3T4zPBNHl9HBA6PfZFHxe8NAoBoJ
+3do1Tu+6Sfy3raH0/6g47nq6+GFEQp2rGnzX/1WEXe0m5qPhjFg4MUOKXkq
h2TNkZDFJgrWPBocr55moWYoj0jIaSUuP3r5tNlPCfWR5JHnksIg6yp8H3eX
R1bGWbnuETo2vlEK3FvDwpaSD4MKM3OEvkN5nIe5CnpvFMUHidLRuejeG7yb
ignZVK+HZkIY/Md1TowhjPT1treLXv4kEu3FBjk8aXhEfGR02glgV+zP/L2H
KLD3m3d+el4Q3ixW+RN9Jva8Yuy8YbhIpP5j+907TBjVVULH1DRpeFJtMTnV
LAMB72/LmRoyWEU+uNt8hozPIV/mY6s/ExLuwo9z+H6cmzpTUFNKRbHgfY+n
9lzgqqnQ3gQ1LJHGRNefkEFww2FRDxIdg3IGpn2Lklhl4dusPSGF/I7ozrxK
GowU9P29NGeI1MqJ82M+HNx5nl/btV8M0you7L5wEuor/9j1lc6/7/lK+2UW
F55BhT66HAl41030ptVI4fEWfa+7n7mYm1cWjSEpYEA0JTODKoqRArEDq9Yp
w2zgx6rHx8QwkHh7y1/+KnC43eo/9YOM3KGMnvRVVCB4bqPLy89EjE7k2Rgl
OhD+LsmV2URM2sTbc7OYEPri2GkONj6dfD/0bocC/iUg51JuK4iW4gVH73Qp
GKlvnFRsVER0uNCxXHFl+AfvCgyI5SJq/cnxZztVwJiv+JDMoeDlp+TQTdUr
oGaWrLMYOUEszf3iu9VJGdoeGjom2lQcrriN99pkXGWrxX84OEtMU+j5qV5S
2PMpy6R/gg6fDMNc9Qg2SI/6Q9cWCUGWfKdLJpuC8rHlc2XlotjTYF20vp2M
Kk+rJ1tWLxOndv+k5riQcVxmevtDgYfE7zom/+zWUMJ1L5M1R3toWBylxnAM
xJA7J7OW2ThE/HpE68SJTYpISVGzU1seI5iyEaZHp8m4dSk+51WkJHReVb4O
eaWIa+1UpUOODESR/zZwZiuD+2CzmxrrLRF6oOpK3qwixOIOznaFUSGVuWr/
izwyimyTlnFUHLNvTvnET8lDrfGL2x4JEvrevVzpvE0Uj5hIOdfCwODrmoLk
E/II2/a73fYaeVzrYbbrOUiAfChu4cphBh6vvTp6zp4N+Uvbr9r6ySCvmHzc
fAcT+qmGSYl3lwnP2Oh+7SEaNqW9dso9OkOcMP8YJibDhXZq+OJbJzW4tK96
VxAuhdxK8/V3zSYIE0Hheq+9VCSHdr1B9HeCYV/mZ13Cw2dpj9DmJyy0HLao
03UTQNHZHVkVxDciS3L6RQdTgq9jxXRoMBteMSGhEW+k0DusptB3i4myGvmE
Ut8VSHYrb/R/K4PN0Wa2vjxV2EQ0etx8L45dVnsOBTmQsGV0ytryiQwi7bPt
WmzosOWot2zi88S69BPj8iYODtV+SXKZpqDn8L3D3lNMiAR6Jr0VXSK0syso
s5uYqEmrnDlBGSFyy6KWj1M5yJGrOlebKoTvO/HQqFMU6Zz0rmJbJr7o/LY/
UpaD6I6cg2Gegjg2auJZqC4Os9VamYkUJWyTPxKvpS6NG+EiKd/aZoj2Id2v
Z3qEIKAQaW16gQTF+Hukix48JOb6X7mpQ4Xi2Ki2BI8N/bz9VZa+FCQbmp4W
NFTA+pibLDldPoeMY2RMlcTxxvsf7ejI70Rp0Ca37HEmaKvB490Xx5EEvwtR
bSqglfpKpH6lY8Gf1BrsLAbbabEClWh5SNeabhDcooIVBfVGLCcOHgjSg6aC
lLB1MpCZXSaO08ZLZZfvMjBGvZjxUI2D9VfLJ+6GyeKNgY5hZrYQiva4u/ce
lYJubsDaYGMuVp89faBYUBbJ1lnJvo0zROXvZZWXullY4fwuZh9BQ466ffUG
Pn+tS3ff7Lz/nXgfp2eqX8hGVT5z5XWNAcLrWYGdcDXfH6pe66o/McBt7is/
p7oCJCuf28X32gi1benhaR+V0Wg+4JXykIzZvcyaW1aqmP+3+ou+F/L/5+J+
/UqbnDt0fNQr2rJcx+8t11nFQyt+EOcnj/coB9BgULdTN6BeBhf05ntPX1PB
49C6gt3pVGQ76OaLnGOAUfJQteGFEipm50ckMtkoklrZMvVeCQTh/kBLVQo3
GEZGzcemCBEFsTYndQ5uXG0oPMfvL8Vu3Q8rB+m4khFaahdIxp/qYysP9DDR
ekq9LbOOibdfNIbW8ij4JfDwrnVN/Bw2Cpq+oacMz9qgQPM8/v8+O15/bZIB
ttP0BctbkuCOOY53bWJh4tBXnU+n2omtwbleQacUIVLlkMjhsbB5H8eJOSMP
78Irmsb8nlSWPTN42oeLXklTvdhYFoIqp2itf3MR7e1k/ac/BwEZFxcktVQg
ZmF6wCKPh4GYnmcufF/0eFgKVKqvwF0FqfNZG1TQU3hcIbZeEvssd2ubOfJg
6xygGmrznZjalJzUZqQKXbsL3cP9XJB2i9cckVRFcpCxo4+hKDqThAIS3Jmo
bzir9HOACb/+RTqTnwfc4dBcJzIXe5INnRtGKVjdIFj5vJqB/J2SmlWCHEyK
98r7TgtiaduvDZ/5+bcYJZ/ow3/PDy2pBqfHxOD5+VZovKIKrnSmBX4s4CI5
3nzKtYGO8Ygs/W1aFLj2vNvpNiKLfa9kLq6yksLztTJ0831MZDwQNTYYYUH/
FUW2N2qOOPONRT6ZR4KrXm1n8gMl1FTUhM9LyEMipzNeZn6MiKXvn290VMRg
ZOurFEM56F3RrjK7yEOz4eV2iz4p5HStqWWwFTBd5OXydZ0S3IVVTb17uKDd
q9jZESiCM9IJlyw3i0A51LOjn02BlaRlnLEADf3kXRZ/JNCwjt3dsrmDDVe1
l799UF8mRnwebbUfVsGa82t3DKWJocR/y10pOUkUeRY2VxxnY+3riEUHaUX8
zNn7889rotBXN0g0/YufD8JLZw+9V8ZI6fXkCH0+n6NMw7jeSsj3s7F7WMPv
x26MUt1WBvwjm6VOl/H9MsEqMA5hYu/iNY/NaTJ4Pvx1uxCfb1ARiK7U42Ag
Nlc77RQVG1RW7vhoqYKUD2N3NsQNEQuNvqyA+wqwqeWs3EVjwa9k4PriCBML
aQc/luTKY6HGlhGuPU1saOyYNoriQrKGIVGXQIZEocGHo6I0JJVo1/7mSMIb
Rs4xmx2KOJWtWVZ+WQURFmXGwuKSmDR6sGwbIoz/AIzvW44=
"], {
{Hue[0.63, 0.7, 0.5], Opacity[0.7], Arrowheads[0.], ArrowBox[CompressedData["
1:eJwVxfk/2g8DAPCtyyxUamq1vq3mGCpyH31TWRgtN1E5om++zmKJ0pzrYE+p
HJ8YNpvWLBEppFBb/BHPH/O8nvcvb7J0rEkKevTo0X/Bjx79/8dPHxc8Hnw8
BYKAECAM6CWoCjQN+gBaBe2DTkEXoCAYDqaCeeBqMB/cB9aCF8BbYD84BIFB
EBAMJA/ChsggA5AJiBHyDXIBCUJh0EQoAoqBEqBsKA9aA62H9kH7oTKoDroA
1UON0C1YHCwRhoBhYAQYGyaD6WBG2A7sABaMI8Sx45rj5HG6OGOcKc4St/4E
9WTvifPJdbwwXh5virfEH8dHnhY+HXz6/ukUHAmnwhlwPlwCl8I34Q64G+6B
++EheBgeTUhKSE54lTCfcJJwlRBOxCQSEnmJfYnyRF2iJfEg6VVSbdJ80mbS
l6SrpDACg8hDsBE8RBWiHiFDTCD0iC3EPhKHJCMZSCaSi+QjpUgFUoXUIA1I
K9KGBJAOpAvpQfqQAWQIxUAxUVKUCuVA7aL2UE6UC+VBXaOiyUXJlcmtyb3J
R8knaBwaj85Av0bT0U1oEVqJ1qB/oAPoWwwBw8bwMDKMDqPHGDE7mOCz1Get
z9qeeVNIKTkp5SltKR0p4pTBlO0UL5aIpWAzsTQsCyvANmDbsRLsMFaN1WJn
sLPYZawZa8fGcHgcGUfHMXFcXBNOhFPglDgNzoCz4mw4AOfC+XAB3O3zd88/
Pd97/h2fgafj8/FNeBFegVfiNXgr3obfwAP4AP6WwCbICTqCkWAiWAjrhB3C
wYvsF29frLxYI1KIVGIpkUUUECXEHqKaqCXOEpeJZqKd+JnoJsb+uvvrnpRD
qiEJSWKSnKQj6Ukm0jppmxR5+eHl6ssLMpPMJTeRRWQpWUFWkQ1kgOwg75Kd
ZBc5QL6lUCmlFAFFQumlqClaip1ySDminFBir/5+9U9qdmpR6tvU1tS2tPS0
grSStMa07rTJtMO087TLtIf0zPSCdEF6d7o63Z5+mP47/SGDnlGWUZHRmTGW
oczYyDh7/ea16PWP138yaZmsTEFme2Z35nDmTKY9M5ZVlsXJasgazTrLuswu
yq7Jfptdn92WPZ69ku2lVlMlVC11k+qmnlD91BA1TI3R8mksWgNtiDZM09IW
aR9pZpqddkOL0bl0EV1BV9I1dCvdRt+gA/RATnlOTY4wR5wjzzHlbOdEcjm5
zbktuV25o7lLuT8ZTAafIWWoGAYGwHAwnAwXw83wMPyMa0Y0rypPljeQ9y3v
Ir8hX5lvzrfmA/mOgpKCxoLBgsmCqYLzgofC8sLKwsbCjsLBwveFU4VHhd6i
4qLWov6i8eL+4vHiheK14q2SxpLBksmSqZLzUklpT6m6dLn0pIxT1lnWVTZa
dlbeWN5WLizvKBeXD5Zvl3uZXCafKWWqmNPMOaaBCTCdTBfTw/Qx7/7+hyVg
tbOGWWrWDGuWZWbZWTesWEVzRWfFWMVGxQFbxh5g69h6tpG9w6njtHA6OV2c
Uc4S55hzxrnkNnFFXClXwVVxNVwD18YFuLtcJ9fF9XED3FvuXWVrZW/l+8qj
N4tvPr758eYPr4/Xz5PxxnkLPD1vi7dfNVI1XbVatV91URWsllT3VWurF6r9
1aGa+pq2GnHNRI2+ZrvG+3bl7VptT+187WbtVW24brRusm6p7rjuki/l9/Gn
+Qa+lW/jb/H9/NC7vXff3/16dy1oF0gEvQK1YFZgFxwKYvWy+vH6iXp9/UqD
tsHcYG2wN9w0xBqFjYONk43HjeeNkSZRk6IJaAo03Ta3NHc2W5oPmn+2dLZ0
tYy2/Gw5a/W2eduH22faZ9vtwg6hWCgXmoQW4bpwW3gsjHSIO/o7tju8HZHO
rs7RzrHOM5FCpBRpRIAoILoVy8Um8bbYK45IeiRqiVZilrglJxK/JCyJdY12
/ew667Z3H3afd192P/Qs95h7Nns+97h7Yr3q3qPe31KFVCU1SAGpQ7ordUpd
Uo/0WhrtW+gL9Y/3L/Rv9XtlA7IJmU6mlxnlOrlJbpGvy4/lkQHjwLeBi39n
/10enBoaHpoZWhz6OHQz9Gd4Znhx+GZkemRu5NPI15H90aXRs9HLsY2xA4VS
oVJoFAaFTQEoXAqfIqC4VWqUVqVNuaEElIHxhXH9+Nr41oR+YuX91PsjlUEF
qByqXZVT5VJ5VNeq6OTS5PHk+eTl5INaq7arD9VH6tj03PT+tG86qDForBqb
ZkMDaHyagNastWvdWr82pI3N3Oj0OqPOpLPo1j+sftj5cPohOLs892nu69z+
/Ob8l/mr+fCCfmFr8ePizeKfpeOl86VLvdFgMwAGp8Fl8BkChjvDvXHdZDGt
m7ZNkZW1T18/7f/nt9lh/mx2m2/MMcu65cASWT1d9a0GV++tNitgdVhDtg0b
YDu1+WwBW8h+aI+tfd042HRv+jevNsObUcABuIAAEHK4HG6HxxHd2t/yb3u3
I5/dOwc7pzvBXeeua/d67/ve9Zdf+8FvF99/OV1Oj/PaGf3xx+VxBVzRw6PD
B7fH7XeH3VF37OjEc+2JHl8eR07Cp77T4Om9L+C7892fP/hD/nDg9iJ4+XAV
vo7exO7u/wdsDP26
"], 0.0665496087165601]},
{Hue[0.63, 0.26, 0.89], EdgeForm[{Hue[0.63, 0.7, 0.33], Opacity[
0.95]}], DiskBox[1, 0.0665496087165601], DiskBox[2, 0.0665496087165601], DiskBox[3, 0.0665496087165601], DiskBox[4, 0.0665496087165601], DiskBox[5, 0.0665496087165601], DiskBox[6, 0.0665496087165601], DiskBox[7, 0.0665496087165601], DiskBox[8, 0.0665496087165601], DiskBox[9, 0.0665496087165601], DiskBox[10, 0.0665496087165601], DiskBox[11, 0.0665496087165601], DiskBox[12, 0.0665496087165601], DiskBox[13, 0.0665496087165601], DiskBox[14, 0.0665496087165601], DiskBox[15, 0.0665496087165601], DiskBox[16, 0.0665496087165601], DiskBox[17, 0.0665496087165601], DiskBox[18, 0.0665496087165601], DiskBox[19, 0.0665496087165601], DiskBox[20, 0.0665496087165601], DiskBox[21, 0.0665496087165601], DiskBox[22, 0.0665496087165601], DiskBox[23, 0.0665496087165601], DiskBox[24, 0.0665496087165601], DiskBox[25, 0.0665496087165601], DiskBox[26, 0.0665496087165601], DiskBox[27, 0.0665496087165601], DiskBox[28, 0.0665496087165601], DiskBox[29, 0.0665496087165601], DiskBox[30, 0.0665496087165601], DiskBox[31, 0.0665496087165601], DiskBox[32, 0.0665496087165601], DiskBox[33, 0.0665496087165601], DiskBox[34, 0.0665496087165601], DiskBox[35, 0.0665496087165601], DiskBox[36, 0.0665496087165601], DiskBox[37, 0.0665496087165601], DiskBox[38, 0.0665496087165601], DiskBox[39, 0.0665496087165601], DiskBox[40, 0.0665496087165601], DiskBox[41, 0.0665496087165601], DiskBox[42, 0.0665496087165601], DiskBox[43, 0.0665496087165601], DiskBox[44, 0.0665496087165601], DiskBox[45, 0.0665496087165601], DiskBox[46, 0.0665496087165601], DiskBox[47, 0.0665496087165601], DiskBox[48, 0.0665496087165601], DiskBox[49, 0.0665496087165601], DiskBox[50, 0.0665496087165601], DiskBox[51, 0.0665496087165601], DiskBox[52, 0.0665496087165601], DiskBox[53, 0.0665496087165601], DiskBox[54, 0.0665496087165601], DiskBox[55, 0.0665496087165601], DiskBox[56, 0.0665496087165601], DiskBox[57, 0.0665496087165601], DiskBox[58, 0.0665496087165601], DiskBox[59, 0.0665496087165601], DiskBox[60, 0.0665496087165601], DiskBox[61, 0.0665496087165601], DiskBox[62, 0.0665496087165601], DiskBox[63, 0.0665496087165601], DiskBox[64, 0.0665496087165601], DiskBox[65, 0.0665496087165601], DiskBox[66, 0.0665496087165601], DiskBox[67, 0.0665496087165601], DiskBox[68, 0.0665496087165601], DiskBox[69, 0.0665496087165601], DiskBox[70, 0.0665496087165601], DiskBox[71, 0.0665496087165601], DiskBox[72, 0.0665496087165601], DiskBox[73, 0.0665496087165601], DiskBox[74, 0.0665496087165601], DiskBox[75, 0.0665496087165601], DiskBox[76, 0.0665496087165601], DiskBox[77, 0.0665496087165601], DiskBox[78, 0.0665496087165601], DiskBox[79, 0.0665496087165601], DiskBox[80, 0.0665496087165601], DiskBox[81, 0.0665496087165601], DiskBox[82, 0.0665496087165601], DiskBox[83, 0.0665496087165601], DiskBox[84, 0.0665496087165601], DiskBox[85, 0.0665496087165601], DiskBox[86, 0.0665496087165601], DiskBox[87, 0.0665496087165601], DiskBox[88, 0.0665496087165601], DiskBox[89, 0.0665496087165601], DiskBox[90, 0.0665496087165601], DiskBox[91, 0.0665496087165601], DiskBox[92, 0.0665496087165601], DiskBox[93, 0.0665496087165601], DiskBox[94, 0.0665496087165601], DiskBox[95, 0.0665496087165601], DiskBox[96, 0.0665496087165601], DiskBox[97, 0.0665496087165601], DiskBox[98, 0.0665496087165601], DiskBox[99, 0.0665496087165601], DiskBox[100, 0.0665496087165601], DiskBox[101, 0.0665496087165601], DiskBox[102, 0.0665496087165601], DiskBox[103, 0.0665496087165601], DiskBox[104, 0.0665496087165601], DiskBox[105, 0.0665496087165601], DiskBox[106, 0.0665496087165601], DiskBox[107, 0.0665496087165601], DiskBox[108, 0.0665496087165601], DiskBox[109, 0.0665496087165601], DiskBox[110, 0.0665496087165601], DiskBox[111, 0.0665496087165601], DiskBox[112, 0.0665496087165601], DiskBox[113, 0.0665496087165601], DiskBox[114, 0.0665496087165601], DiskBox[115, 0.0665496087165601], DiskBox[116, 0.0665496087165601], DiskBox[117, 0.0665496087165601], DiskBox[118, 0.0665496087165601], DiskBox[119, 0.0665496087165601], DiskBox[120, 0.0665496087165601], DiskBox[121, 0.0665496087165601], DiskBox[122, 0.0665496087165601], DiskBox[123, 0.0665496087165601], DiskBox[124, 0.0665496087165601], DiskBox[125, 0.0665496087165601], DiskBox[126, 0.0665496087165601], DiskBox[127, 0.0665496087165601], DiskBox[128, 0.0665496087165601], DiskBox[129, 0.0665496087165601], DiskBox[130, 0.0665496087165601], DiskBox[131, 0.0665496087165601], DiskBox[132, 0.0665496087165601], DiskBox[133, 0.0665496087165601], DiskBox[134, 0.0665496087165601], DiskBox[135, 0.0665496087165601], DiskBox[136, 0.0665496087165601], DiskBox[137, 0.0665496087165601], DiskBox[138, 0.0665496087165601], DiskBox[139, 0.0665496087165601], DiskBox[140, 0.0665496087165601], DiskBox[141, 0.0665496087165601], DiskBox[142, 0.0665496087165601], DiskBox[143, 0.0665496087165601], DiskBox[144, 0.0665496087165601], DiskBox[145, 0.0665496087165601], DiskBox[146, 0.0665496087165601], DiskBox[147, 0.0665496087165601], DiskBox[148, 0.0665496087165601], DiskBox[149, 0.0665496087165601], DiskBox[150, 0.0665496087165601], DiskBox[151, 0.0665496087165601], DiskBox[152, 0.0665496087165601], DiskBox[153, 0.0665496087165601], DiskBox[154, 0.0665496087165601], DiskBox[155, 0.0665496087165601], DiskBox[156, 0.0665496087165601], DiskBox[157, 0.0665496087165601], DiskBox[158, 0.0665496087165601], DiskBox[159, 0.0665496087165601], DiskBox[160, 0.0665496087165601], DiskBox[161, 0.0665496087165601], DiskBox[162, 0.0665496087165601], DiskBox[163, 0.0665496087165601], DiskBox[164, 0.0665496087165601], DiskBox[165, 0.0665496087165601], DiskBox[166, 0.0665496087165601], DiskBox[167, 0.0665496087165601], DiskBox[168, 0.0665496087165601], DiskBox[169, 0.0665496087165601], DiskBox[170, 0.0665496087165601], DiskBox[171, 0.0665496087165601], DiskBox[172, 0.0665496087165601], DiskBox[173, 0.0665496087165601], DiskBox[174, 0.0665496087165601], DiskBox[175, 0.0665496087165601], DiskBox[176, 0.0665496087165601], DiskBox[177, 0.0665496087165601], DiskBox[178, 0.0665496087165601], DiskBox[179, 0.0665496087165601], DiskBox[180, 0.0665496087165601], DiskBox[181, 0.0665496087165601], DiskBox[182, 0.0665496087165601], DiskBox[183, 0.0665496087165601], DiskBox[184, 0.0665496087165601], DiskBox[185, 0.0665496087165601], DiskBox[186, 0.0665496087165601], DiskBox[187, 0.0665496087165601], DiskBox[188, 0.0665496087165601], DiskBox[189, 0.0665496087165601], DiskBox[190, 0.0665496087165601], DiskBox[191, 0.0665496087165601], DiskBox[192, 0.0665496087165601], DiskBox[193, 0.0665496087165601], DiskBox[194, 0.0665496087165601], DiskBox[195, 0.0665496087165601], DiskBox[196, 0.0665496087165601], DiskBox[197, 0.0665496087165601], DiskBox[198, 0.0665496087165601], DiskBox[199, 0.0665496087165601], DiskBox[200, 0.0665496087165601]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{223.890625, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/38af1deb5f692d5f.png)
|
| In[22]:= |
|
| Out[22]= |
|
Show the geodesic balls with radii up to 3 as a highlighted graph:
| In[23]:= |
![ResourceFunction[
"WolframHausdorffDimension"][graph3D, {0.9977324444882885`, 0.2066910739888672`, 0.3244588909666948`}, 3, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/7ff103b2a33c9839.png)
|
| Out[23]= |
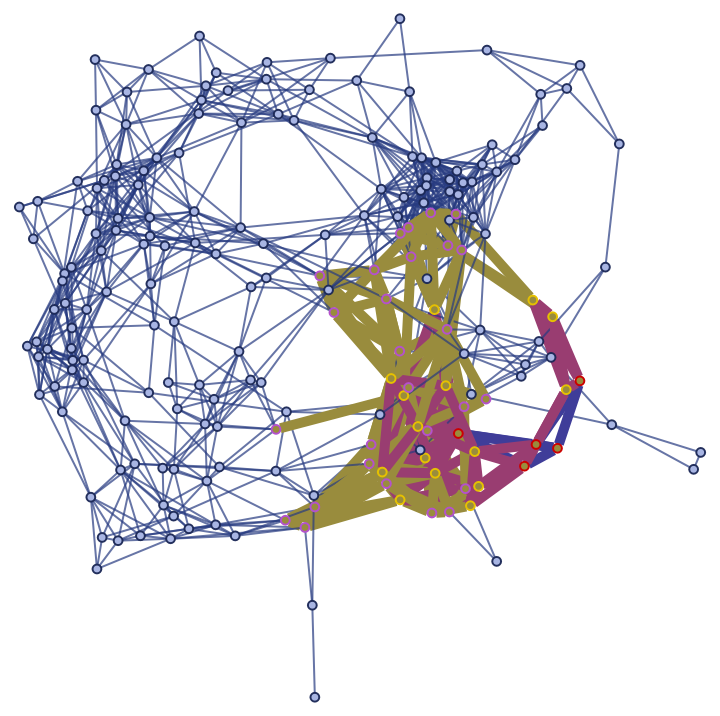
|
Compute the Wolfram–Hausdorff dimension at an arbitrary vertex in an approximately 4-dimensional graph (produced using FlatManifoldToGraph):
| In[24]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/73af2894-e2b8-4cd0-821b-36f28c703a4c"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/63ab7b1de627594e.png)
|
| In[25]:= |
|
| Out[25]= |
|
Show the geodesic balls with radii up to 3 as a highlighted graph:
| In[26]:= |
![ResourceFunction[
"WolframHausdorffDimension"][graph4D, {0.4696085959869871`, 0.9931506580784377`, 0.9678518484665577`, 0.5187881757568464`}, 3, "HighlightedGraph"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/63842c71f1587d63.png)
|
| Out[26]= |

|
If given a graph, WolframHausdorffDimension returns an Association showing the Wolfram–Hausdorff dimension at each vertex, using the graph radius as the maximum geodesic ball radius:
| In[27]:= |
|
| Out[27]= |

|
| In[28]:= |
|
| Out[28]= |

|
Use geodesic ball radii between 3 and 5 instead:
| In[29]:= |
|
| Out[29]= |

|
If given a graph, a vertex and a maximum radius, WolframHausdorffDimension returns the Wolfram–Hausdorff dimension at that vertex:
| In[30]:= |
|
| Out[30]= |
|
WolframHausdorffDimension also supports directed graphs:
| In[31]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAYA7mmYAq3T8IxMSUWUrvP5TMvnnQ
Lu4/LPamrnjK7j9QXnoCq1nTPzg1VJeN3t0/gKRhpA6Prz+MxpBJZq7YP6jd
7/Z4gts/NlJMenjr6D8g1/Po3OCoP0D+PCTDGuQ/FFsxworK0T+wlLzYgBi3
P4zmzJ7/DOw/kJ1Jc3Huuz9gxKG6LALRP3RBVtc/Ze0/CEUth86/xT8AmE9j
+X25P9iRiKm5F94/0CMkyq3O2T90KAweOhfvP1wVFVHLJ9Q/6BGcj40ZwD94
UfWCtWzRP0JdY8FIYuM/GsVMrRV/5T9os9Hh/gbPP8CLTPixed8/mOCTVqED
4j/EeX89A5PhP6gzJK2w0t4//qPE3b2d5D+4SkeOJ7naP2bh/wlxi+Y/vJjb
NDrD7j/UanOC/evsP+CtTggX2+s/aPfhhZE25D/MNKin
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 3, 5, 6, 7, 10, 11, 11, 11, 14, 14, 16, 17, 19, 20,
21, 23, 25, 28, 30, 31}, {{5}, {12}, {14}, {16}, {19}, {
13}, {13}, {4}, {17}, {18}, {4}, {6}, {17}, {18}, {7}, {
10}, {8}, {7}, {10}, {16}, {13}, {8}, {11}, {13}, {16}, {
3}, {15}, {16}, {11}, {20}, {12}}}, Pattern}], Null}, {
EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJx1lg9YTOkex2em+adppj9T4ZLIpa2UFpVcvK9N6Fnh6Q+yl6ehWhtLLN0N
Udom8l9ZlM2VNnFx++OixHtWi8rfohRl8y+SmD/NaKZpus055z3z7Dz290zP
22fO+877nt/3+z3PGbV8bVgsh8VivR74M41/LkdI/0NQgx3NCkB/T7MQfp7t
/uJ7BbLYiLDgv1iPC69nzkF8/lwMsz5/TsvftTwnc15gsZ74PDPrabazYKEF
W+7P9Bf9eT7zOxbz8bks+8T0F0rflH1xZX4VOrwx61LKHSkcfHUhjN3bgGxb
ivYK90hhhE9v6u3m52jlRJh+eIYUjvju2Npy0Tt0fHNUrvc7B5iYkTFp63kl
unih+0Gt3AG27PMIqG3XovPP7MeuHewAfw+9gIjzBiTXFef87Zg9/LlN+sY3
jU1M49X73HW0hyLNjJJGLZd4xN74Qp5qBzn5nuGqozxiiS1HGiKzg9YFZzNa
PfjElcmt70dOsYNuvbfmHSnkE7pkfoLExg6GnNpS5GYnIEZd6508+rwtTC2q
zd4SJyCEl+WvIvxtYY2xRFp4WkAUdpx7UVIsgSPPTBhzvFlAGMLWTZziIoE7
zsyt+VYrIKy7HzR2bRYz/Z9Ilgj2kyUg6tyT692TrZnr64ffWjf81iDIpllq
b6pBzPVi3jcDH7OeC/QF8/UFAoY/fjAVn+G9LycPfMzs07Tdu2k7j+FJ5Hms
4MFIJ9DcIyCWPfQcMyKFA+ctjDTEvBQQubXJlZp6NhzPIQJOIgGhGDJOV+7F
hn5RkcqsPQJi8TW/p/GZLLjiGyePgFABcXaj3w27Z/3gspD1x24jn6gffnHE
mDIjmCRzkh46wSfc1nddd8juAw0xkTfm+/OJ3I1PS5pTDCBPSmgqK3nEdPeU
zqSkXsC/H3oipplLSPJyv6op1YEtAfd5znwuoVuTJxpn0wP65s4cXfeVFdF7
dMes/HQtyLQ9pzu0j0NIXZeovVw1wG3boJ0x79lEsNHBoaZJDapzo+qmRrGJ
/QFl+UmlKpAU+0v9iEYWoaqd8uu0s0oQ0PJot/UKFvH95dNDnW6a83v62/cv
NPeljP8XF9hMbc0xs83FaNHFaDNXHXu7IGWUmbeSCxwYBh1Z0zuyzMydf6k9
I9jMd3ZKeENU9gznHDWVmd+Zlk83cyApMJNDVuYOU5mZlNvbzJRfbBlWkH6R
MEz5xcyUX8QM371jKhuGyfYMM7NedmCCYoOI4Z9M2zdZM0zdr5k33/RZ1l85
iGHq/sxMTq81P3/O+rpPcYwWwlN5Jbseg34Ufr/pRudxW7jctO0qIyqZM/TH
Cj9bSJ27Dw1Z/Zvz6t8k0OaH/CC23IDSA+tOsIIkkDpnLzIUmxaIIdmW+Xq0
td4USDE0qezqrEP8vDV3bXfZwC9N21Z/QkekLta+r0Qwjiwtwnk+SS7vRjjP
ZBv3qhHO82g3U6kQzrNMZDKOAuE8U774gHCeK6+YqhPhPFM6v0U4z6TtRO0I
55k6x0tEynOHC8n2rG1DcaQ+XHjPdld26qmniLpvKziY7EsjovThQFPXwLh6
ROnDgUWksLfRJlIfNsw2ydJRhSh92LCto3GgdeWI0ocFjZ4m5xYhSh8W/A+t
E9YH64j16aB1xvpgH2B9sE+wPmm0j7A+2GdYn5W0D7E+2KdYn+njwgamiiHW
59HERKX+jRhiffbRvsf6rPpHTssimQRifeJpxvrgnGB9Gunfw/pAej+sDz4P
1gfnBuuD7wfrg3OD9cH9wPrgfmF9cG6wPrjfWB+cG6wPzhOdI+Z5R+eIYTpH
DNM5YpjOkZmpHJnnUzlimM4Rw3SOQHXHbpfNg9cjF79jkq08Dc0HUfU9p0xV
hRqwM6anxi8pGHhfeNhUJVfR10vRp+WP9MqVShDiPW5Z8cxKtHnpUMUWmYKe
/zt6HjxzXU3bB6C/AdK7y26jC3GtRWFeXfT6erTKxSg/lN8Jni+Kq7v0uhEJ
4wtFB2e9A1Gjrf7rrH6JwtZsLdrAbwcApO7SVHciWTSYkj7sBXiAnMHUTUoU
k1KfmiFqBdNUaVX3K7qRfFjPj9GZjeCtvzDcr/ATGn/wY9Shsgegfs/JrtVT
9aiiel3IXMkt0KONzEpMNqDAOQtiv3asBMvWu84M+86IvJ4Irz2NPw1wfiLI
/AgYPUvJ/AiY/FA55jN+kJP54TN+6SPzw7PID4/xm5DMD5fJz1EyP1aMX/H7
QWfFgrGKVWI4JmfO6j9SOFC+JmFdUKsYlr/ubtI3sOG/33idvzlSAlVOk5PS
J7DhxLFpLUn+EnjP0yF0288sGOSZaPjnCAmc9/e0iLdsFqxXcyUJTWL4guvs
mtphBE+2j7cvixHDhMxwg+2zPiB7rOGNrbKBs5uvweTnBrBCueh9tVoEqbEX
VLC31a2WWkNq1IM5Gdxgj4VCSI09QLT97SzjFT6kRi3gqDwfd87kQWrUAN/H
tzVKhRWkRjXI/vJ2vh3BgdSoAt5sj2ezS9mQGpXAEPz61OFbLEiNCnBw9sL2
d4H9qGa01w+aYwIo8bux5Hq4Ee3IWe793EMA11fPXSoP7UOBMYU+VYV8WMnu
6vJ3N6BnKdrEXCkfdrX9avOoTY8SFWH8+AQeFMT9q3zpJh3ill1p8bnKhcID
su6H6k/op2pffYfOCqpkMVf9Q7VI51u6LHesFbzetM1RLu9GsvfAOiiIAyP8
IzdGZ6nRhGAH9yzEhkemNTQ3VKrQx1k787R+bLj/Q/+Mdo4KHVEWJHxfyIKB
IQ3nDsQqkWdw7C+f7FjwUGikS9MrBVqQlh3i2WkEBb3b9penKJDbvVPi3UV9
IDY8UuAfqEDV8dwMxyUG8CSiITVUokCzo878r6of512BqPcVHcOkfQN6GFZX
ucW2dWgBm2aB6fFarGGuC0g/djOs2b200pikZpi0b7KKYXJ6tpLhxbJ5G74g
FOD/jiRXzA==
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 5}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 12}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{1, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 14}], 0.043048128342245986`], ArrowBox[BezierCurveBox[{2, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 16}], 0.043048128342245986`], ArrowBox[{2, 19}, 0.043048128342245986`], ArrowBox[{3, 13}, 0.043048128342245986`], ArrowBox[{4, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{5, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 4}], 0.043048128342245986`], ArrowBox[{5, 17}, 0.043048128342245986`], ArrowBox[{5, 18}, 0.043048128342245986`], ArrowBox[{6, 4}, 0.043048128342245986`], ArrowBox[{9, 6}, 0.043048128342245986`], ArrowBox[{9, 17}, 0.043048128342245986`], ArrowBox[{9, 18}, 0.043048128342245986`], ArrowBox[{11, 7}, 0.043048128342245986`], ArrowBox[{11, 10}, 0.043048128342245986`], ArrowBox[{12, 8}, 0.043048128342245986`], ArrowBox[{13, 7}, 0.043048128342245986`], ArrowBox[{13, 10}, 0.043048128342245986`], ArrowBox[{14, 16}, 0.043048128342245986`], ArrowBox[{15, 13}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{16, 152, 153, 154, 155, 156, 157,
158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 8}], 0.043048128342245986`], ArrowBox[{16, 11}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{17, 178, 179, 180, 181, 182, 183,
184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 13}], 0.043048128342245986`], ArrowBox[{17, 16}, 0.043048128342245986`], ArrowBox[{18, 3}, 0.043048128342245986`], ArrowBox[{18, 15}, 0.043048128342245986`], ArrowBox[{18, 16}, 0.043048128342245986`], ArrowBox[BezierCurveBox[{19, 204, 205, 206, 207, 208, 209,
210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 11}], 0.043048128342245986`], ArrowBox[{19, 20}, 0.043048128342245986`], ArrowBox[{20, 12}, 0.043048128342245986`]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.043048128342245986], DiskBox[2, 0.043048128342245986], DiskBox[3, 0.043048128342245986], DiskBox[4, 0.043048128342245986], DiskBox[5, 0.043048128342245986], DiskBox[6, 0.043048128342245986], DiskBox[7, 0.043048128342245986], DiskBox[8, 0.043048128342245986], DiskBox[9, 0.043048128342245986], DiskBox[10, 0.043048128342245986], DiskBox[11, 0.043048128342245986], DiskBox[12, 0.043048128342245986], DiskBox[13, 0.043048128342245986], DiskBox[14, 0.043048128342245986], DiskBox[15, 0.043048128342245986], DiskBox[16, 0.043048128342245986], DiskBox[17, 0.043048128342245986], DiskBox[18, 0.043048128342245986], DiskBox[19, 0.043048128342245986], DiskBox[20, 0.043048128342245986]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{229.61328125, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/2e026e6302471fd7.png)
|
| In[32]:= |
|
| Out[32]= |
|
In the directed case, the Wolfram–Hausdorff dimension is computed using volumes of geodesic cones, as opposed to geodesic balls:
| In[33]:= |
|
| Out[33]= |
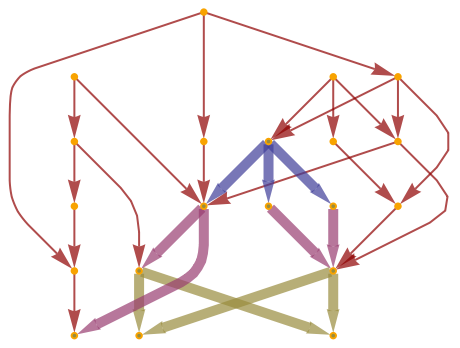
|
However, WolframHausdorffDimension can be made to treat directed graphs as though they were undirected (and hence revert to using geodesic balls) with the option "UndirectedGraph":
| In[34]:= |
|
| Out[34]= |
|
| In[35]:= |
|
| Out[35]= |
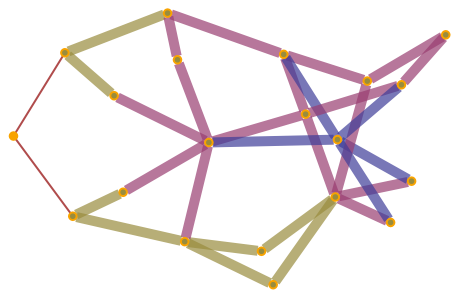
|
WolframHausdorffDimension also supports dimension computations in graphs with non-integer dimensionality, such as this Sierpinski sieve graph:
| In[36]:= |
|
| Out[36]= |
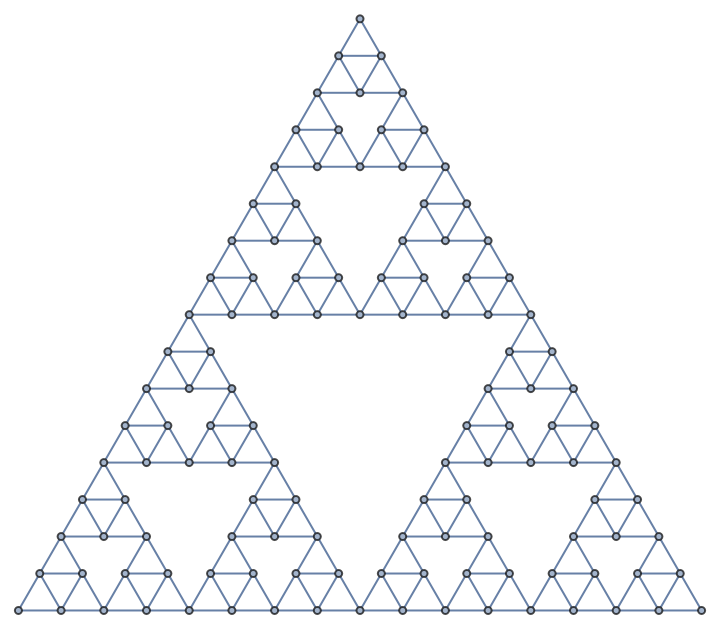
|
| In[37]:= |
|
| Out[37]= |
|
| In[38]:= |
|
| Out[38]= |
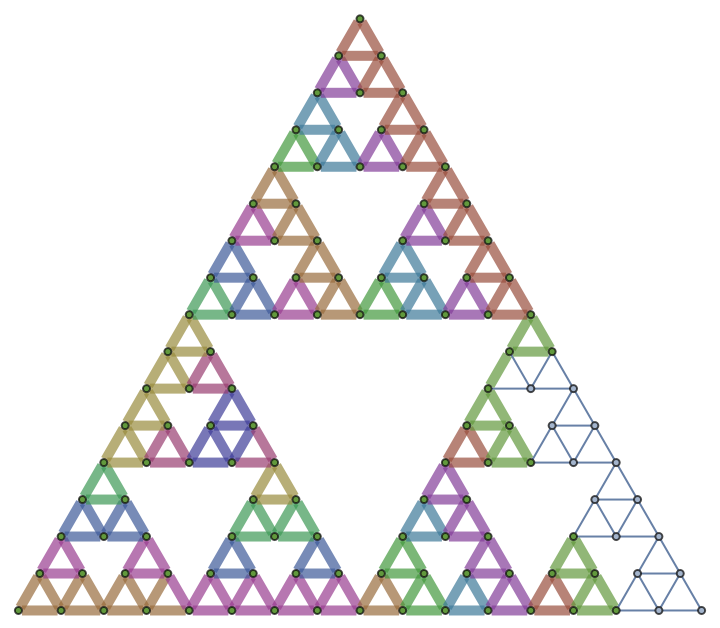
|
Compute the average Wolfram–Hausdorff dimension for geodesic balls around vertex 150 with radii between 3 and 9 in a 20-by-20 2-dimensional grid graph with the option value "DimensionMethod"→Mean (default):
| In[39]:= |
|
| Out[39]= |

|
| In[40]:= |
|
| Out[40]= |
|
Return a list of all dimensions for geodesic balls with radii between 3 and 9 instead:
| In[41]:= |
|
| Out[41]= |
|
Compute the maximum and minimum dimensions for geodesic balls with radii between 3 and 9 with the option values "DimensionMethod"→Max and "DimensionMethod"→Min, respectively:
| In[42]:= |
|
| Out[42]= |
|
| In[43]:= |
|
| Out[43]= |
|
By default, directed graphs are not transitively-reduced:
| In[44]:= |
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/35350ecf-8893-48d2-af98-f2ad1e4a6e00"]](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/00f5bb836c9972b4.png)
|
Compute (and visualize) the Wolfram–Hausdorff dimension, assuming that the graph is not transitively-reduced:
| In[45]:= |
|
| Out[45]= |
|
| In[46]:= |
|
| Out[46]= |

|
WolframHausdorffDimension can be made to treat unreduced directed graphs as though they were transitively-reduced with the option "TransitivelyReduce":
| In[47]:= |
|
| Out[47]= |
|
| In[48]:= |
|
| Out[48]= |
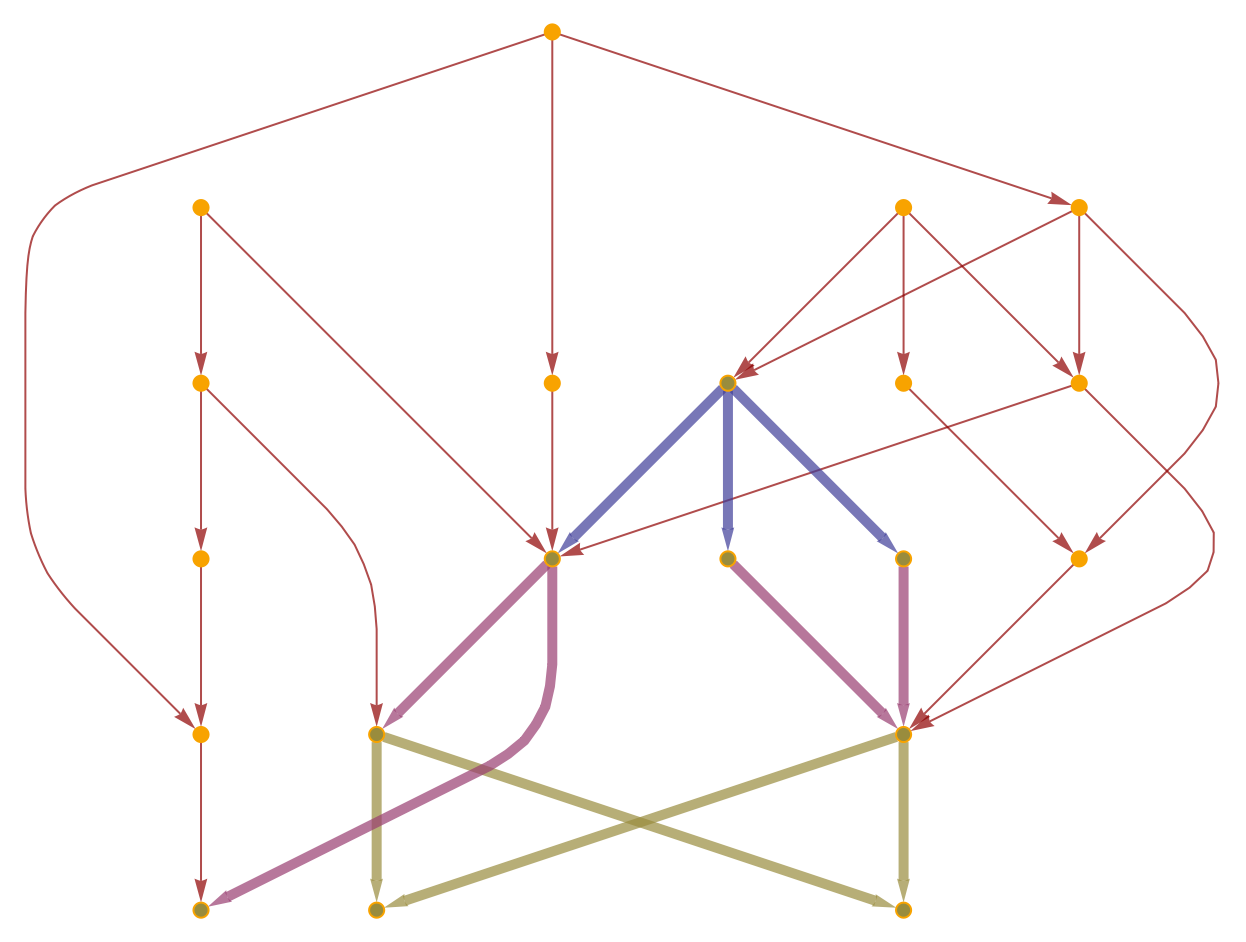
|
By default, directed graphs are treated as directed (and so dimension computations use the volumes of geodesic cones, as opposed to geodesic balls):
| In[49]:= |
![directedGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[CompressedData["
1:eJwBUQGu/iFib1JlAgAAABQAAAACAAAAiBDgQC0N7D8Miwlf7rPgP2DD6g69
ErY/vFne0Lkv2D8AYqEgHNmHP0y+xxYqrO0/sBJhl3Rm4T9kbie+Xq3eP6hf
tX6aZ88/ki5iaxFR6D/KvOcIEIXvPyB5b3EiyMs/gEqJn4lg3T8W9qyLs0/s
P7qg/i7vruI/SMlbtu/k0D9I3gFvCW3tP1AaT8UdINs/TnYI2uGX7z/A7Age
bdDiP9B5FJWzMrU/DqNXMXBJ6T+sgi4Z70bmP85zrMZJD+g/cMA/h/uy2T/K
qgmYaj/kP1ycpAlxYeo/MJn6j48Euz9cbg+fJinePwzPqiEI19M/Siz/TIYE
6T/4ia6W8rHLP0BF9wTPFcs/riH/Ot0j7D/kWXJEIx/aP6SzChO3t+U/Pmkf
1Khk6z+AomBv3AKAP+Ys8tyO2+Q/SIuN6pq61D85Ap6m
"], {
SparseArray[
Automatic, {20, 20}, 0, {
1, {{0, 1, 1, 3, 7, 12, 13, 16, 16, 18, 19, 23, 25, 26, 27,
27, 28, 30, 31, 31, 32}, {{9}, {11}, {14}, {8}, {15}, {
16}, {20}, {2}, {8}, {15}, {16}, {20}, {19}, {2}, {9}, {
18}, {6}, {16}, {9}, {2}, {8}, {15}, {19}, {1}, {4}, {
4}, {19}, {14}, {5}, {18}, {13}, {14}}}, Pattern}], Null}, {EdgeStyle -> {
Hue[0, 1, 0.56]}, VertexStyle -> {
Directive[
Hue[0.11, 1, 0.97],
EdgeForm[{
Hue[0.11, 1, 0.97],
Opacity[1]}]]}}]]},
TagBox[GraphicsGroupBox[GraphicsComplexBox[CompressedData["
1:eJxdmAs0lFsbx2cMc3GZGc2YmZKD41upSUihInvnlm50SEUlHF1IQn2OkCLX
cupDKEpRSaWSOiVHZpcuKIlKnE5FEXIb19zna+Y17yyeNWs96zf79rz73fv/
PDPanvscd8gRCAQVIoEg9lONCTFPRZNfTPJsNLWdMMnUSWZOY9wmWQgwz5tk
9rT5pSYdLxRMXU/aX9oujY89LZ7p8UnXlcaHxyOYtj6aGp+Up8+P27T5pPtD
ncbTn08aj9RL58fjnMb4fsJp8cCp/XnT1pMyPg+a2l+6H+xpzIQiiakjp6q6
p+3nGfjz3LabGVxkLGOe7yOO7yM6ztFLq7MIVjIeyxcPUME5vEb3UI2ujMmZ
fpWM48o4n2ZpKBo2KeG8SGJKeDzV4uGHFPH2wNnPA2Y/p+HMUhWbjPMVtvz8
yN7H+pFLDiOXKDh3d4mNjPOJr0t+fmSsXxe5oC5SAefFknhIsH9+5RnFUXWU
/DhdZ1W0HKy9tXgXv0Md+ccuv5fVQoQXjpvs3v5GHVVFqLebuxKhs6Dm7NV8
dXT99uLHsz4S4MBqmgItSh1RufFmZv4EeET/nwuH1qmjptu8TZksAuz3tvGn
qKijMPnn8+JOiMCG8dX7cx7PQkbMN22bOSKQ2fr9qqvfLNQc49x1s2QCVJGX
nHF15aLLS5JD7OzGQC6RU7Uqjo02EIMDs8gjYH591Jq5Q6pI2ECqfTD8A1yZ
RdPocGKgoPcmlxO1B8Eac77hTjMl9L2J2TA3vB9A7t7XJTkUtJaWFHOY0Qei
rlePD6TIo7PWRadT3vWAWcObCpVocqguNZ6z57X0fBEIVzJvH38PRDh7JhoJ
D+yZwBnbz3GclfdnWxFjxnAe8RAPGJWx+HU5jMj6m39M1+QM47xQdxnbvewH
zjslNgjK2hI0QrmBAg3js/RwhYFJThKUvVI71lvUB4ixFhE+rpcEuxe9qSuN
6Z1sLxD88Hw70rO7B6xaoOeWb10sCN02UxjmIZzs/0TQaGMdUN7QBUaeguj+
Oy8Ed3d+zHWc3zk5vkawR2MiJiW7HTRu2ll9v7lWQPXJUUqy/Q5cdEi3OH1f
BY5+4bkHyN8AABHHB8raBR7uYFm0+hfwWsAB5iE9Aq8jNRGxSh/B8t6jpVVF
/YIY9aFg92O1oNWE6mSc80NgkNTtknLnNaj582Knr/mIoKgsYNVa+nMwNOic
HHRoTLDUbv2ONexi4Baoae3oPSGY/w+15IPPVVxvru7q+DJQxYVSdrkk3lEu
JE6y8j13pXvusvbSs63rj2jL+PBm8QAOzqAt2aItWcbyDve/xdrIuDKersDr
VcM5/YzYZCwZbiHjpZILyMbjiY8Tm0wf68XHZ4GM54rloIaFc/AfYpOxWB0C
ZsuYK9GrGdPiUcX5uyQeGWPxMPF4jknikemz5DgvkDGmLwychRJ9oeOM6YuM
sfuggrNU73IKYCuq6wZ9cWf6X0cpwrMVclmk37vB0IUlI6iZBj+ttOWXZXaB
FaFMa9JGGvTlK0XREzpBBVe7Ju0dFdoF/nazlt8BTgf5XAr3osJAzZlXtUK/
g9y0jqL7clT4faHngY6wVjAackXNKp8C86/qMZcZfgNJWhl3tfZS4KOY4DBa
ylfgG/c8bf1SCnxt+KajzyMOvFw8GsYjk2GqN8Fd3qxRsGtY9MChQx7Osf8t
ft0FoWB57Tv7wXYSvHF55n8y3/8QrH4RZqasQIKeZi6EA1YTglN1/YcTTeXg
RQr1ZEsPEfEmls+OOUqE15nnSzZtlUfvzDYzv7cSYEVhzwlFDzJ6lWi19eEu
AvQtvDpT7ZkQNCWmPAh5xYW9FcsuL8/rAdbrbqcKT3Hh/0zvZB8s6AUaRk5p
Hk5caDMxY0Z5XR/YB0P/rqRxIUvTtW++5gAwD55HMi7kwJEzcbbZ0YMgsn6b
X5obBw75ZSrpKQ8BKy/eeP+YGmRkZliWFwyDQzyXW+uS1aCF7pH2gwdHwcJB
zegsbTWYV37t2HnfMXDm1/jk8s9suOsxfw7fahwEX7R2GE1nw0BVQsnM8XFQ
GexYaOLEhmX3+I5+6RMgNbvgVSiVDX0Lrn3RVReBt1o7kiqKWHCb/JF9todF
IK7Pm6Tjw4IZedeGyp+JQMGsR9rRHBbUvc4PL+gRAcdUn06hQHp+CVB6fjn7
v0S1dorAKpUrR7evUIWuL+NZ2fd/jt8fnV3cxYQVSoPX9baJwIeXiwfzs5jQ
a6GufdynCVDC+yvc3JUJ9ZZrjNw1mwDbN5HNt/OYUMug7lbBgXFwUPW3rUaF
DLiCsnlfRPwYyHMxvfZ2NQOeeHp2iXbIKNgaK/C43EqHmM6NgMj0tshLiXSI
6dwgSMnQ5J+LUIGYzvUCXt1J+8YYZYjpXCegr18m9M9SgpjOfQOBJE3G2mpF
iOlcA7DtXX49kKMIMZ17DxJmpz1p8qdBTOdeAstI/pbsBirEdO4B8NYZ8ru+
gwpn+fnYRi9ko3Kd+fsHzlJgcYG9N2MPG8Wley5onEeBzZV5uzPz2GipV45+
aQ4ZJgqirI0G2ejTkcGgDBYZPo2tHatYqYaChI5kH38FGD4nO3F3lhqSv/P3
v/oP5WFJRoucEomDosoMR9qGSTCqJWd9gS8HDRsWuGXMIcEqWkOI2ycO8ugA
ilZWctBH8r65yMhmhm6ygAjT84/FV6znom7b+MxBY+Lk++ei0z2X/PfmEGDB
jWOnMnK4iG+z49wPJmHyPHDR+qOnVvHbJwCP2JBR/ZmLfn11RSUhdxxg54OL
ynzkY9muY6BCcjy5aKXLtb9KRdL8yUPS/OjEoWrwRrmoRXVRWxZtAGxw0Trg
3vEznhUB/REv+sBYmZ1C/RsuOjyoFUfO6wX2OyJeR9zmomQDy0sG13/mR/2K
d67RXKTf+dZuvEwIunR01LwcuMjBoP6/+xSEwMI24cQ5Bhd1tJ/bqPyoC5ik
KFhSnnGQXaRvTeTdTlDHPGmQFchB+dq/bLds7gBp3oPDhspsJJEZXit41Sva
f75OFWU0i1osbn8F3Zs3mdXfYqCPt28GFWz/DPgL+joN2cpog+u3Dx5z64CD
5xuRzScqOvckR3S8uBq4Df3w59HJKKjxc6nHkjKwodt9Re5FEsoNoShZajwE
JivpAQOZROS5v4m5qfsqwOpLCsLyozRfUJEk3aWzJvWfirD8KGvH8qOMwyUD
ZuCMJTgZY/lRxi8l+VEVZ+l9TnJWA/VDFHTLO2UGA6pC+43OY15fKci+2eJT
SBsTGsgh04sCCjqonDr2bwoTGrs49yT/SUF6n9P3Gtsw4e9b1OaZrqOg2qJ0
T2o3AxZSCZ8TJsjIh77lZJILAy72UGOlZJER80GQB62CDt95OT91MPmpt0Wd
db6QDjNZaKC4WAGdl3gVSK5al+VVL48wrwzDTKsUOGR5hHllOL7WWqfakoQm
JF4JHmPcGE45KYcwrwh/PUyL9+ogIh2Jp8GyDJdqcxciwjwNHtxxruaXWgLC
PBWa/vs2QfF3AsI8FVbbCj9ufEFAa7qO2vErufCovPM960dE1FDiU3PzJBfy
lurHlzfKob8D7p77cyUXJjSFbmzWk0efyB7XnvVz4BeyxS+nsxWQXbj/kEsa
B/IuHGhotKSgkfdfYlcacKBhvua5xyo01M8q3HyyWA3yTcGGZSQlZGIk9FkI
1KC88RuFVToqSGB0vGTB/Z967ml/lvlQBTmaazncOM6GWaS8+8iajvhOTddS
XNkwiduxyaWIjmz+eF/9TYcNUzPph/7RYKDs3OHSCy0sWHCapWu9j4EsW1ZH
lF5mwSaFUefUmww0Z9ELmoMbC+p9e0Kr/sBA9gkh26xUWTBhaYBl/yADPejd
HHahRHp+mGhq/cJEU+sXJppavzDR1PqFiabWL0w0tX5hoqn1CxNNrV+YaGr9
wkSVL8WmjLPkOqnLGKvvlfB4osTL1yni7dj9kHHoM303UTENZ+z5ZCzpXiH7
/yHPUPyDgAr/D/YhGQA=
"], {
{Hue[0, 1, 0.56], Opacity[0.7], Arrowheads[Medium], ArrowBox[{1, 9}, 0.05783410138248847], ArrowBox[{3, 11}, 0.05783410138248847], ArrowBox[BezierCurveBox[{3, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 14}], 0.05783410138248847], ArrowBox[{4, 8}, 0.05783410138248847], ArrowBox[{4, 15}, 0.05783410138248847], ArrowBox[{4, 16}, 0.05783410138248847], ArrowBox[{4, 20}, 0.05783410138248847], ArrowBox[{5, 2}, 0.05783410138248847], ArrowBox[{5, 8}, 0.05783410138248847], ArrowBox[{5, 15}, 0.05783410138248847], ArrowBox[{5, 16}, 0.05783410138248847], ArrowBox[{5, 20}, 0.05783410138248847], ArrowBox[BezierCurveBox[{6, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 19}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 2}], 0.05783410138248847], ArrowBox[BezierCurveBox[{7, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 9}], 0.05783410138248847], ArrowBox[{7, 18}, 0.05783410138248847], ArrowBox[{9, 6}, 0.05783410138248847], ArrowBox[{9, 16}, 0.05783410138248847], ArrowBox[{10, 9}, 0.05783410138248847], ArrowBox[{11, 2}, 0.05783410138248847], ArrowBox[{11, 8}, 0.05783410138248847], ArrowBox[{11, 15}, 0.05783410138248847], ArrowBox[BezierCurveBox[{11, 174, 175, 176, 177, 178, 179,
180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 19}], 0.05783410138248847], ArrowBox[{12, 1}, 0.05783410138248847], ArrowBox[BezierCurveBox[{12, 209, 210, 211, 212, 213, 214,
215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 4}], 0.05783410138248847], ArrowBox[{13, 4}, 0.05783410138248847], ArrowBox[{14, 19}, 0.05783410138248847], ArrowBox[{16, 14}, 0.05783410138248847], ArrowBox[BezierCurveBox[{17, 235, 236, 237, 238, 239, 240,
241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 5}], 0.05783410138248847], ArrowBox[{17, 18}, 0.05783410138248847], ArrowBox[{18, 13}, 0.05783410138248847], ArrowBox[{20, 14}, 0.05783410138248847]},
{Hue[0.11, 1, 0.97], EdgeForm[{Hue[0.11, 1, 0.97], Opacity[1]}], DiskBox[1, 0.05783410138248847], DiskBox[2, 0.05783410138248847], DiskBox[3, 0.05783410138248847], DiskBox[4, 0.05783410138248847], DiskBox[5, 0.05783410138248847], DiskBox[6, 0.05783410138248847], DiskBox[7, 0.05783410138248847], DiskBox[8, 0.05783410138248847], DiskBox[9, 0.05783410138248847], DiskBox[10, 0.05783410138248847], DiskBox[11, 0.05783410138248847], DiskBox[12, 0.05783410138248847], DiskBox[13, 0.05783410138248847], DiskBox[14, 0.05783410138248847], DiskBox[15, 0.05783410138248847], DiskBox[16, 0.05783410138248847], DiskBox[17, 0.05783410138248847], DiskBox[18, 0.05783410138248847], DiskBox[19, 0.05783410138248847], DiskBox[20, 0.05783410138248847]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{273.59375, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/9e3/9e31c8fd-d724-4dae-87f0-96f6c1e99fd2/182852a3c4a3b0e9.png)
|
Compute (and visualize) the Wolfram–Hausdorff dimension, assuming that the graph is directed:
| In[50]:= |
|
| Out[50]= |
|
| In[51]:= |
|
| Out[51]= |
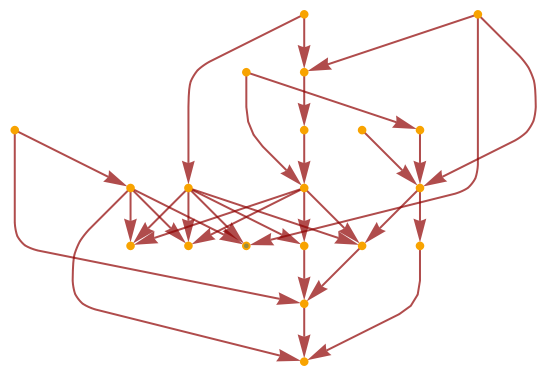
|
WolframHausdorffDimension can be made to treat directed graphs as though they were undirected with the option "UndirectedGraph":
| In[52]:= |
|
| Out[52]= |
|
| In[53]:= |
|
| Out[53]= |
|
Return an Association showing the geodesic ball volumes around each vertex in a 20-by-20 2-dimensional grid graph (default):
| In[54]:= |
|
| Out[54]= |

|
| In[55]:= |
|
| Out[55]= |

|
Compute the average ball volume across all vertices with the option value "VertexMethod"→Mean:
| In[56]:= |
|
| Out[56]= |
|
Compute the maximum and minimum ball volumes across all vertices with the option values "VertexMethod"→Max and "VertexMethod"→Min, respectively:
| In[57]:= |
|
| Out[57]= |
|
| In[58]:= |
|
| Out[58]= |
|
Return an Association showing the Wolfram–Hausdorff dimension at each vertex in a 20-by-20 2-dimensional grid graph (default):
| In[59]:= |
|
| Out[59]= |

|
| In[60]:= |
|
| Out[60]= |

|
Compute the average dimension across all vertices with the option value "VertexMethod"→Mean:
| In[61]:= |
|
| Out[61]= |
|
Compute the maximum and minimum dimensions across all vertices with the option values "VertexMethod"→Max and "VertexMethod"→Min, respectively:
| In[62]:= |
|
| Out[62]= |
|
| In[63]:= |
|
| Out[63]= |
|
Compute the average volume of geodesic balls around vertex 150 with radii between 3 and 9 in a 20-by-20 2-dimensional grid graph with the option value "VolumeMethod"→Mean (default):
| In[64]:= |
|
| Out[64]= |

|
| In[65]:= |
|
| Out[65]= |
|
Return a list of volumes of geodesic balls with radii between 3 and 9 instead:
| In[66]:= |
|
| Out[66]= |
|
Compute the maximum and minimum volumes of geodesic balls with radii between 3 and 9 with the option values "VolumeMethod"→Max and "VolumeMethod"→Min, respectively:
| In[67]:= |
|
| Out[67]= |
|
| In[68]:= |
|
| Out[68]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License