Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 WithCachedValues

Source Notebook

Evaluate an expression while temporarily caching results from specified functions

Contributed by: Sjoerd Smit

ResourceFunction["WithCachedValues"][{f1,f2,…},expr]

evaluates expr while temporarily caching values returned by functions fi.

Details and Options

During evaluation of ResourceFunction["WithCachedValues"], the functions fi use memoization of the form fi[args___]:=fi[args]=… to remember computed values.
Once ResourceFunction["WithCachedValues"] finishes, the DownValues of the fi will be restored and the cached values will be discarded. All other assignments made to the fi inside of ResourceFunction["WithCachedValues"] will be discarded as well.
ResourceFunction["WithCachedValues"] has the HoldAll attribute.

Examples

Basic Examples (3) 

Define a function that doesn't evaluate quickly:

In[1]:=
ClearAll[f] f[x_] /; EvenQ[x] := (Pause[1]; Print["Even ", x]; x/2); f[x_] /; OddQ[x] := (Pause[1]; Print["Odd ", x]; 2 x); f[x_] := (Pause[1]; Print["Other ", x]; x)

WithCachedValues can evaluate expressions while automatically remembering function values for f so they only have to be computed once:

In[2]:=
ResourceFunction["WithCachedValues"][{f}, {f[1], f[1], f[2], f[2], f[1], f[2], f[1/2], f[1/2]} ] // AbsoluteTiming
Out[2]=

The function values are only remembered within WithCachedValues and will be cleared after it finishes:

In[3]:=
f[1] // AbsoluteTiming
Out[3]=
In[4]:=
DownValues[f] // TableForm
Out[4]=

Applications (3) 

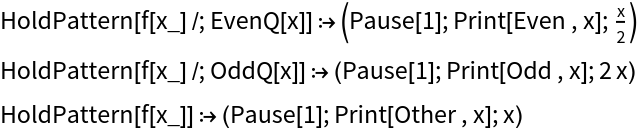When fitting a numerical solution to a differential equation, you may want to cache the solution to reduce the number of calls to NDSolveValue because NonlinearModelFit will call the model many times:

In[5]:=
data = {{6.47, 3.65}, {7.43, 3.45}, {3.9, -2.94}, {4.8, -1.29}, {2.48, -0.35}, {6.32, 3.16}, {2.59, -1.19}, {9.13, -2.}, {3.81, -3.04}, {3.33, -2.68}}; i = 0; model[a_?NumericQ, b_?NumericQ, c_?NumericQ] := Module[{y, x}, i++; NDSolveValue[{y''[x] + a y[x] == 0, y[0] == b, y'[0] == c}, y, {x, 0, 10}] ]; nlm = NonlinearModelFit[data, model[a, b, c][x], {a, b, c}, x, Method -> "Gradient"]; StringForm["Number of calls to NDSolveValue: `1`", i]
Out[9]=

Memoization can be used for the model (as is discussed in the documentation of NonlinearModelFit), but it is unlikely that the cached solutions are of much use after the fit has completed. Instead, cache the NDSolveValue results during the fitting process without storing them permanently:

In[10]:=
i = 0; ResourceFunction["WithCachedValues"][{model}, nlm = NonlinearModelFit[data, model[a, b, c][x], {a, b, c}, x, Method -> "Gradient"] ]; StringForm["Number of calls to NDSolveValue: `1`", i]
Out[12]=

Plot the solution:

In[13]:=
Show[ListPlot[data], Plot[nlm[x], {x, 0, 10}, PlotStyle -> Orange]]
Out[13]=

Possible Issues (1) 

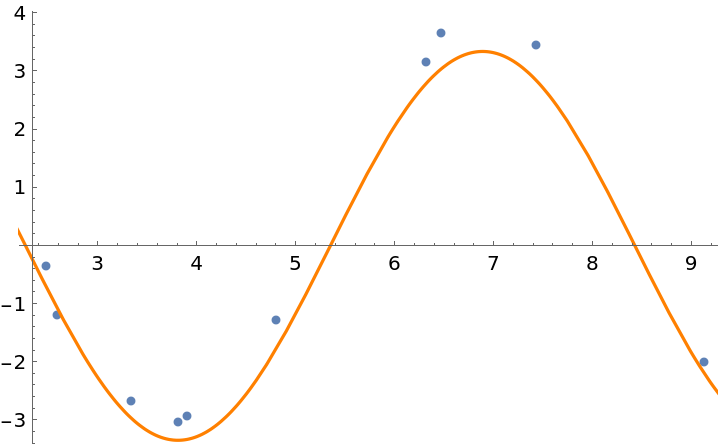All assignments made to cached functions inside of WithCachedValues will be lost afterwards:

In[14]:=
Clear[f]; ResourceFunction["WithCachedValues"][{f}, f[x_] := StringForm["I have a value `1`", x]; f[Pi] ]
Out[15]=
In[16]:=
f[Pi]
Out[16]=

Publisher

Sjoerd Smit

Version History

  • 1.0.0 – 05 October 2020

License Information