Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Transform data such that its covariance matrix is the identity matrix
ResourceFunction["WhiteningTransform"][data] whitens data such that its covariance matrix is the identity matrix. |
Show some original data:
| In[1]:= |
| Out[2]= | 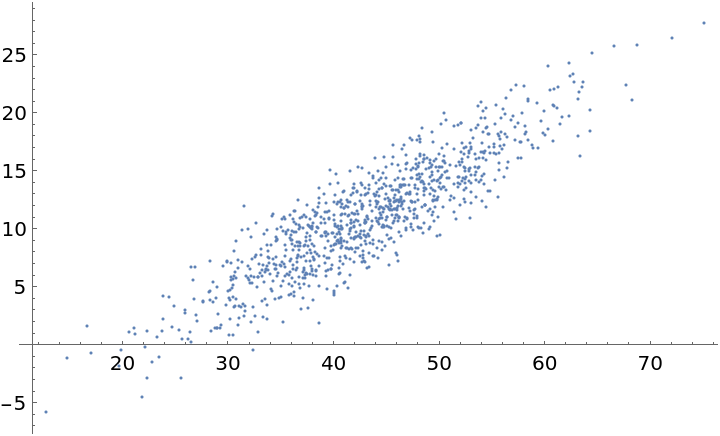 |
Apply the whitening transform and show the result:
| In[3]:= | ![o = ResourceFunction["WhiteningTransform"][x];
ListPlot[o, AspectRatio -> Automatic]](https://www.wolframcloud.com/obj/resourcesystem/images/1e9/1e9daaa6-cf0b-40e2-b832-fab02b1dad67/7d78530174695169.png) |
| Out[4]= | 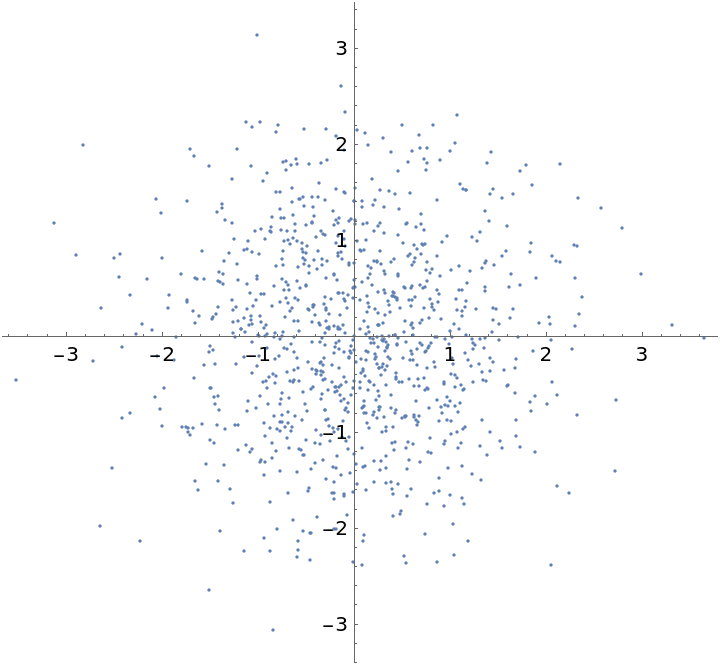 |
Verify that the covariance matrix is an identity matrix (up to small numerical errors):
| In[5]:= |
| Out[5]= |
Data can also be in higher dimensions:
| In[6]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/aeaeecfa-6de9-4010-9ed2-0ad4e639e843"]](https://www.wolframcloud.com/obj/resourcesystem/images/1e9/1e9daaa6-cf0b-40e2-b832-fab02b1dad67/56472df5f25f84f4.png) |
| Out[7]= | 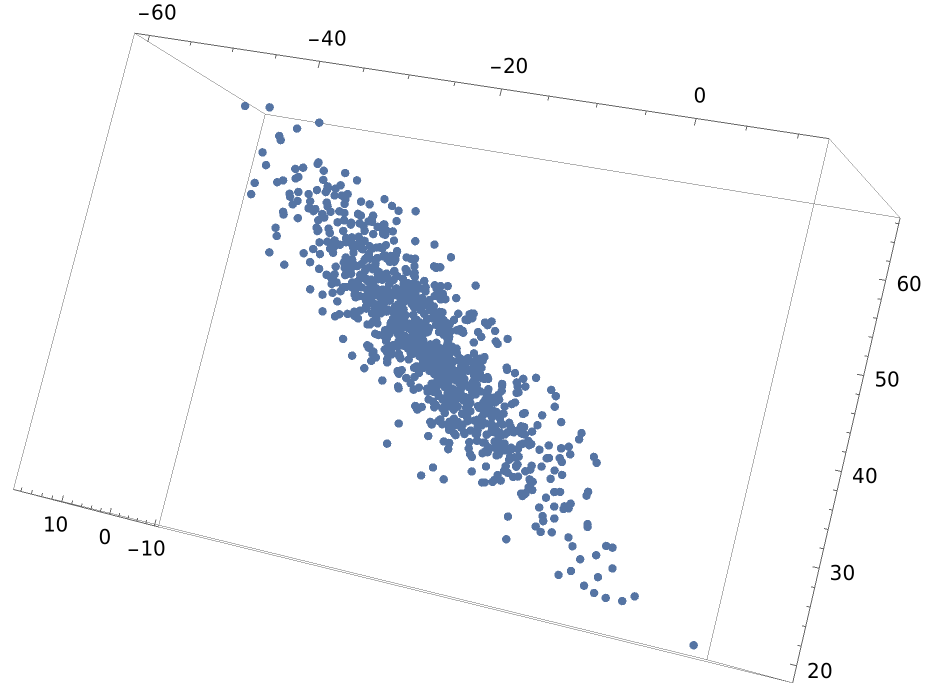 |
Apply the transform:
| In[8]:= |
| Out[9]= | 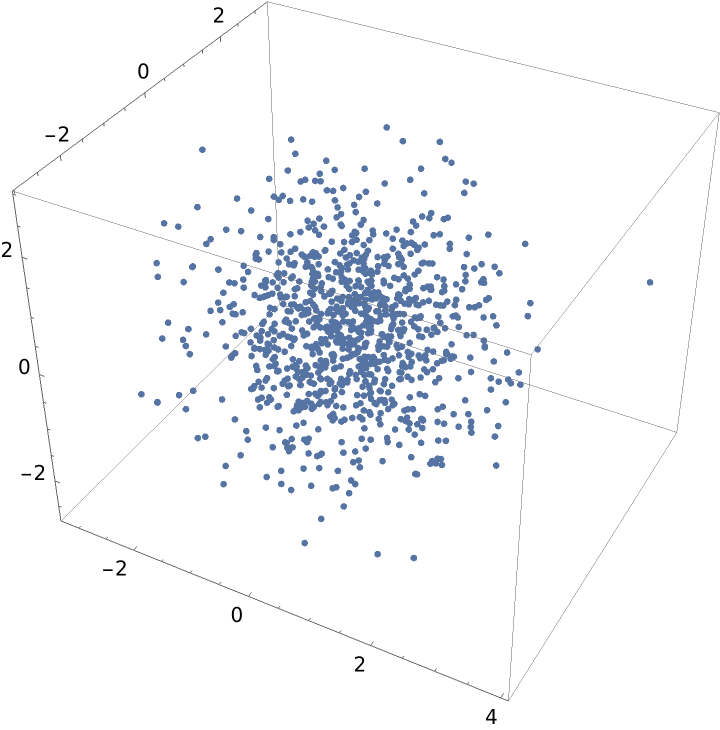 |
Verify that the covariance matrix is the identity matrix up to numerical error:
| In[10]:= |
| Out[10]= |
Use the default method and the "SVD" method and check how far the covariance matrices deviate from the identity matrix:
| In[11]:= | ![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/7a2908c4-bc6c-40e3-aee6-01444659a5ef"]](https://www.wolframcloud.com/obj/resourcesystem/images/1e9/1e9daaa6-cf0b-40e2-b832-fab02b1dad67/408b73c1fe069fee.png) |
| Out[14]= |
Create some 6 dimensional correlated data and visualize it:
| In[15]:= | ![BlockRandom[SeedRandom[12345];
n = 400;
feat = 6;
{\[Mu], \[Sigma]} = {10, 2.5};
X = RandomVariate[NormalDistribution[\[Mu], \[Sigma]], {n, feat}];
scales = RandomSample[N[10^Subdivide[0, 2, feat - 1]]];
scale = DiagonalMatrix[scales];
theta = 0.5 Pi;
rot = RotationMatrix[
theta, {RandomReal[{-1, 1}, feat], RandomReal[{-1, 1}, feat]}];
t = scale . rot;
X = Map[# . t &, X]];
ParallelAxisPlot[X]](https://www.wolframcloud.com/obj/resourcesystem/images/1e9/1e9daaa6-cf0b-40e2-b832-fab02b1dad67/618b5d167d8c2ed7.png) |
| Out[16]= | 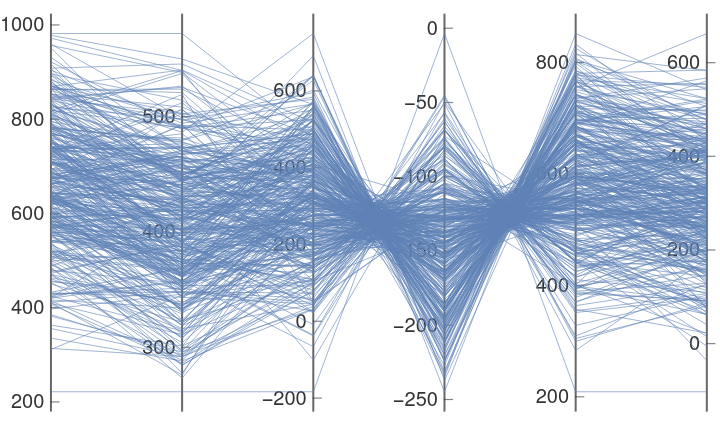 |
Show the plots of 2D projections:
| In[17]:= |
| Out[17]= |  |
Whiten the data and visualize the output to verify that all off-diagonal plots are "sphered" and the diagonals are on a line:
| In[18]:= | ![o = ResourceFunction["WhiteningTransform"][X];
Table[ListPlot[o[[All, {i, j}]], PlotRange -> All, ImageSize -> 80, Axes -> False, AspectRatio -> 1], {i, feat}, {j, feat}] // Grid[#, Frame -> All] &](https://www.wolframcloud.com/obj/resourcesystem/images/1e9/1e9daaa6-cf0b-40e2-b832-fab02b1dad67/5370f06c88dc0c82.png) |
| Out[19]= |  |
Verify that the covariance matrix is the identity matrix:
| In[20]:= |
| Out[20]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License