Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 WeyrDecomposition

Source Notebook

Compute the Weyr decomposition of a square matrix

Contributed by: Jan Mangaldan

ResourceFunction["WeyrDecomposition"][m]

yields the Weyr decomposition of a square matrix m. The result is a list {s,w} where s is a similarity matrix and w is the Weyr canonical form of m.

Details

The Weyr canonical form is also referred to as the modified Jordan form, reordered Jordan form, second Jordan form or H-form.
A matrix in Weyr canonical form is block diagonal, with diagonal blocks called basic Weyr matrices that correspond to a single eigenvalue.
In a basic Weyr matrix corresponding to an eigenvalue λ, the main diagonal blocks are multiples of the identity matrix with λ, the superdiagonal blocks are full column rank matrices in reduced row-echelon form and all other blocks are zero.
The original matrix m is equal to s.w.Inverse[s].
The matrix m can be either exact or symbolic.

Examples

Basic Examples (2) 

Find the Weyr decomposition of a 7×7 matrix:

In[1]:=
ResourceFunction["WeyrDecomposition"][({ {-35, -9, -33, 26, -17, 2, 32}, {-27, -2, -23, 15, -11, 1, 20}, {61, 9, 56, -41, 23, 1, -56}, {-9, 7, -4, 8, 2, -10, 16}, {54, 13, 47, -36, 28, -4, -44}, {60, 2, 49, -42, 19, 12, -64}, {40, -2, 32, -26, 10, 9, -41} })]
Out[1]=

Format the results:

In[2]:=
MatrixForm /@ %
Out[2]=

Scope (2) 

Weyr decomposition of an exact matrix with a deficient eigenspace:

In[3]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{"-", "1"}], "0", "0", "2", "1", "0", "0"}, { RowBox[{"-", "1"}], "0", "0", "1", "1", "0", "0"}, {"6", RowBox[{"-", "2"}], RowBox[{"-", "2"}], "4", "2", RowBox[{"-", "2"}], "4"}, { RowBox[{"-", "2"}], "1", "1", "0", "0", "1", RowBox[{"-", "1"}]}, {"3", RowBox[{"-", "1"}], RowBox[{"-", "1"}], "2", "1", RowBox[{"-", "1"}], "2"}, { RowBox[{"-", "5"}], "2", "2", RowBox[{"-", "5"}], RowBox[{"-", "3"}], "2", RowBox[{"-", "4"}]}, {"2", "0", "0", RowBox[{"-", "4"}], RowBox[{"-", "2"}], "0", "0"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);
In[4]:=
{s, w} = ResourceFunction["WeyrDecomposition"][m];
In[5]:=
MatrixForm /@ {s, w}
Out[5]=

Weyr decomposition of a symbolic matrix:

In[6]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { RowBox[{ RowBox[{"-", "1"}], "+", "u"}], "1", RowBox[{"-", "2"}], RowBox[{"-", "1"}], "2"}, { RowBox[{"u", "-", "v"}], RowBox[{ RowBox[{"-", "u"}], "+", RowBox[{"2", " ", "v"}]}], RowBox[{ RowBox[{"2", " ", "u"}], "-", RowBox[{"2", " ", "v"}]}], RowBox[{"u", "-", "v"}], RowBox[{ RowBox[{ RowBox[{"-", "2"}], " ", "u"}], "+", RowBox[{"2", " ", "v"}]}]}, { RowBox[{ RowBox[{"-", "u"}], "+", "v"}], RowBox[{"1", "+", "u", "-", "v"}], RowBox[{ RowBox[{"-", "u"}], "+", RowBox[{"2", " ", "v"}]}], RowBox[{ RowBox[{"-", "u"}], "+", "v"}], RowBox[{"u", "-", "v"}]}, { RowBox[{ RowBox[{"-", "1"}], "+", "u", "-", "v"}], RowBox[{"1", "-", RowBox[{"2", " ", "u"}], "+", RowBox[{"2", " ", "v"}]}], RowBox[{ RowBox[{"-", "2"}], "+", RowBox[{"2", " ", "u"}], "-", RowBox[{"2", " ", "v"}]}], RowBox[{ RowBox[{"-", "1"}], "+", RowBox[{"2", " ", "u"}], "-", "v"}], RowBox[{"2", "-", RowBox[{"2", " ", "u"}], "+", RowBox[{"2", " ", "v"}]}]}, { RowBox[{ RowBox[{"-", "1"}], "-", "u", "+", "v"}], RowBox[{"2", "+", "u", "-", "v"}], RowBox[{ RowBox[{"-", "2"}], "-", RowBox[{"2", " ", "u"}], "+", RowBox[{"2", " ", "v"}]}], RowBox[{ RowBox[{"-", "1"}], "-", "u", "+", "v"}], RowBox[{"2", "+", RowBox[{"2", " ", "u"}], "-", "v"}]} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);
In[7]:=
{s, w} = ResourceFunction["WeyrDecomposition"][m];
In[8]:=
MatrixForm /@ {s, w}
Out[8]=

Properties and Relations (2) 

WeyrDecomposition[m] gives a matrix factorization of m as s.w.Inverse[s]:

In[9]:=
m = \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"3", RowBox[{"-", "2"}], "3", "2", RowBox[{"-", "3"}]}, {"4", RowBox[{"-", "6"}], "9", "5", RowBox[{"-", "9"}]}, { RowBox[{"-", "4"}], "5", RowBox[{"-", "6"}], RowBox[{"-", "4"}], "5"}, {"2", RowBox[{"-", "4"}], "3", "3", RowBox[{"-", "3"}]}, { RowBox[{"-", "5"}], "7", RowBox[{"-", "11"}], RowBox[{"-", "6"}], "10"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\);

Find the Weyr decomposition:

In[10]:=
{s, w} = ResourceFunction["WeyrDecomposition"][m]
Out[10]=
In[11]:=
Map[MatrixForm, %]
Out[11]=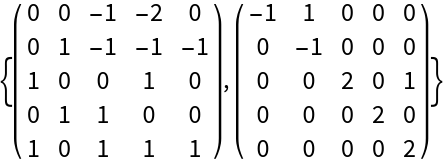

m is equal to s.w.Inverse[s]:

In[12]:=
m == s . w . Inverse[s]
Out[12]=

The eigenvalues of m are on the diagonal of w:

In[13]:=
Eigenvalues[m]
Out[13]=

For matrices that do not have multiple Jordan blocks associated with an eigenvalue, WeyrDecomposition is equivalent to JordanDecomposition:

In[14]:=
m = {{3, 7, -22, -6}, {7, 4, -20, -7}, {0, 0, -3, 0}, {6, 7, -21, -9}};
In[15]:=
MatrixForm /@ ({s, w} = ResourceFunction[ "WeyrDecomposition"][{{3, 7, -22, -6}, {7, 4, -20, -7}, {0, 0, -3, 0}, {6, 7, -21, -9}}])
Out[15]=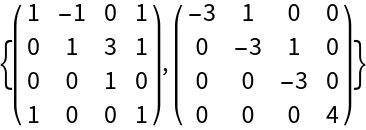
In[16]:=
{s, w} === JordanDecomposition[{{3, 7, -22, -6}, {7, 4, -20, -7}, {0, 0, -3, 0}, {6, 7, -21, -9}}]
Out[16]=

Version History

  • 1.0.0 – 07 February 2022

Source Metadata

License Information