Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Given vertices, get a complete graph with edge weights equal to edge lengths
ResourceFunction["WeightedDistanceGraph"][vert] given the list of vertices vert, returns a graph where edges are vertex pairs weighted by their Euclidean distance. |
The output based on the Kreisel–Kurz integral heptagon looks like a random complete graph:
| In[1]:= | ![pts = (# {1/2227, Sqrt[2002]/2227} & /@
{{0, 0}, {49595290, 0}, {26127018, 932064}, {32142553, 411864}, {17615968, 238464}, {7344908, 411864}, {19079044, -54168}});
g = ResourceFunction["WeightedDistanceGraph"][pts]](https://www.wolframcloud.com/obj/resourcesystem/images/f8a/f8ad35c5-7816-4a0e-ab4f-4bb7a3e2b5fe/6b632b8bfeb0ed83.png) |
| Out[2]= | 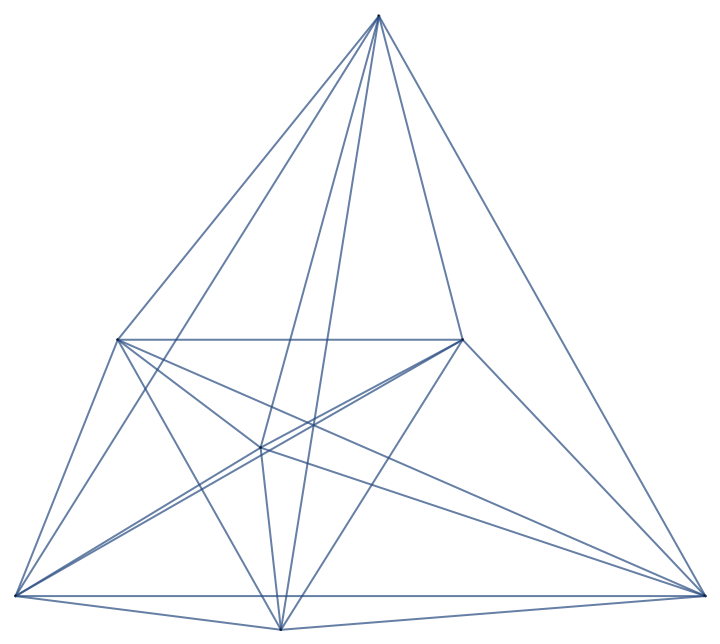 |
The graph has edge weights:
| In[3]:= |
| Out[3]= | 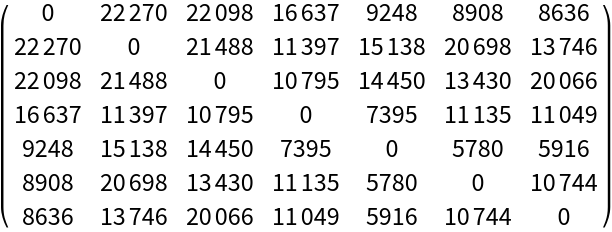 |
The Wolfram Language has several graph functions that work on point sets that do not return weighted graphs. Operations on graphs without proper weighting can return unexpected results:
| In[4]:= | ![v = RandomReal[1, {15, 2}];
g = {ResourceFunction["WeightedDistanceGraph"][v], NearestNeighborGraph[v, 3]};
Grid[{g, FindSpanningTree[#, Method -> "Kruskal"] & /@ g}]](https://www.wolframcloud.com/obj/resourcesystem/images/f8a/f8ad35c5-7816-4a0e-ab4f-4bb7a3e2b5fe/66e2bdd299539dfa.png) |
| Out[4]= |  |
With weights given to edges, a method like Kruskal’s algorithm can work as expected:
| In[5]:= |
| Out[6]= | 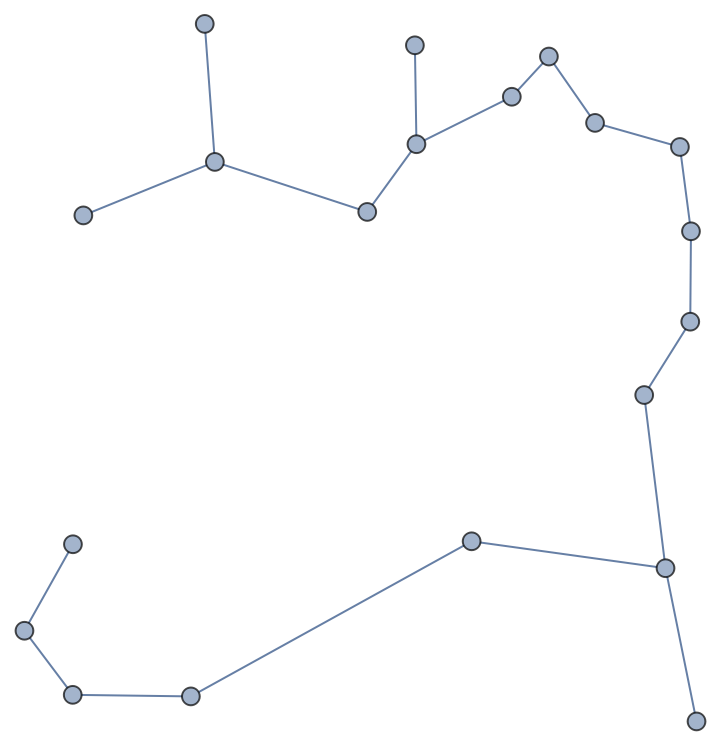 |
With weights given to edges, a method like Prim’s algorithm can work as expected:
| In[7]:= |
| Out[7]= | 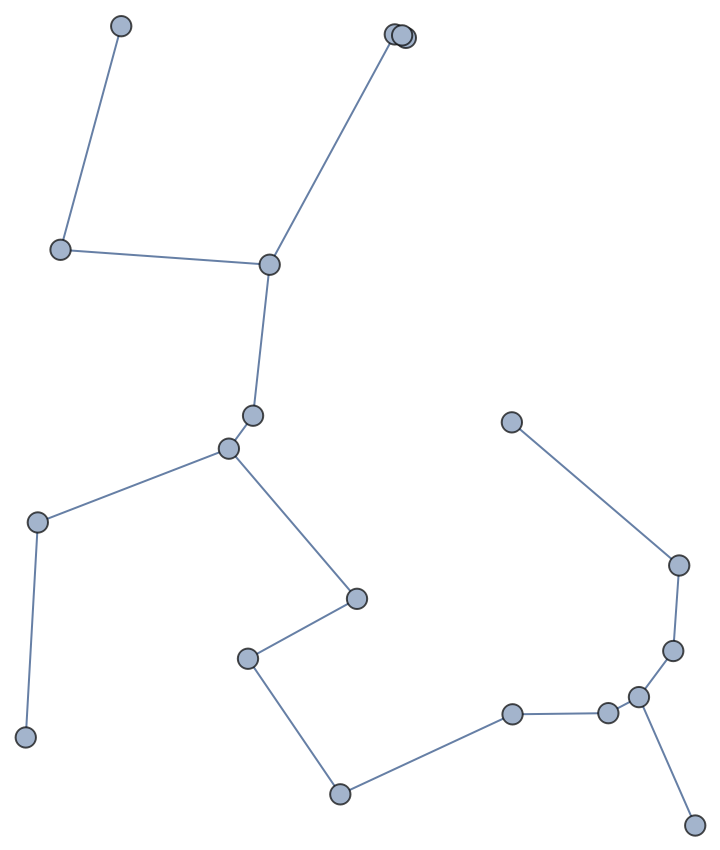 |
Using weighted graphs for finding a minimal spanning tree does not scale up well for larger graphs:
| In[8]:= |
| Out[8]= |  |
In these cases it is better to go right to the algorithm, which is several thousand times faster:
| In[9]:= | ![KruskalAlgorithm[pts_, type_] := Module[{n = Length[pts], vpairs, jj = 0, hh, pair, dist, c1, c2, c1c2, span}, Do[hh[k] = {k}, {k, n}];
vpairs = SortBy[Flatten[
Table[{Norm[pts[[k]] - pts[[l]]], {k, l}}, {k, 1, n - 1}, {l, k + 1, n}], 1], N[#[[1]]] &];
span = First[Last[Reap[While[jj < Length[vpairs], jj++;
{dist, pair} = vpairs[[jj]];
{c1, c2} = {hh[pair[[1]]], hh[pair[[2]]]};
If[c1 =!= c2, Sow[Apply[UndirectedEdge, vpairs[[jj, 2]]]];
c1c2 = Union[c1, c2];
Do[hh[c1c2[[k]]] = c1c2, {k, Length[c1c2]}];
If[Length[hh[pair[[1]]]] == n, Break[]];];]]]];
Which[type === "EdgeList", span, type === "Graph", Graph[span, VertexCoordinates -> Thread[Range[Length[pts]] -> pts]]]];](https://www.wolframcloud.com/obj/resourcesystem/images/f8a/f8ad35c5-7816-4a0e-ab4f-4bb7a3e2b5fe/0374bcb76f1c9fcb.png) |
| In[10]:= |
| Out[10]= |  |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License