Basic Examples (2)
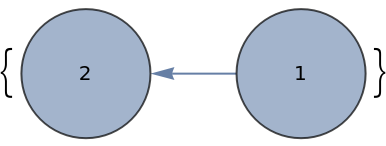
Find a weak path graph for a simple directed graph:
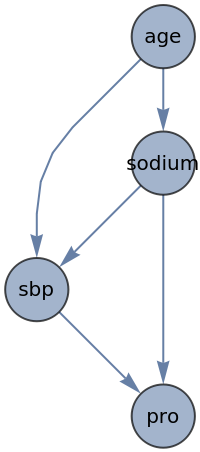
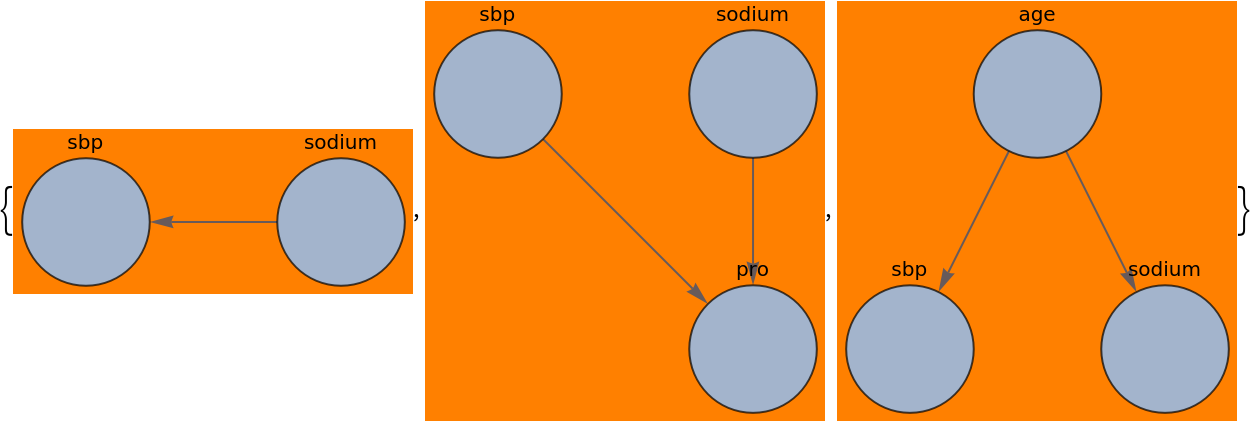
Take a graph and find all paths between "sodium" and "sbp" assuming the graph was undirected, but preserve the direction of the original edges in the resulting "weak path graph":
Scope (6)
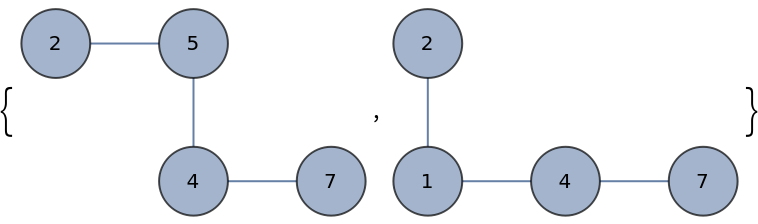
WeakPathGraphs works with undirected graphs:
Same idea but with different options to improve rendering:
Directed graphs:
Multigraphs:
Mixed graphs:
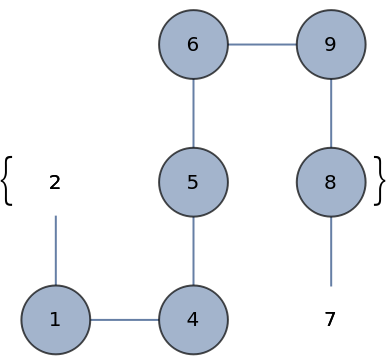
Weighted graphs:
Weighted graphs with EdgeWeight disinherited:
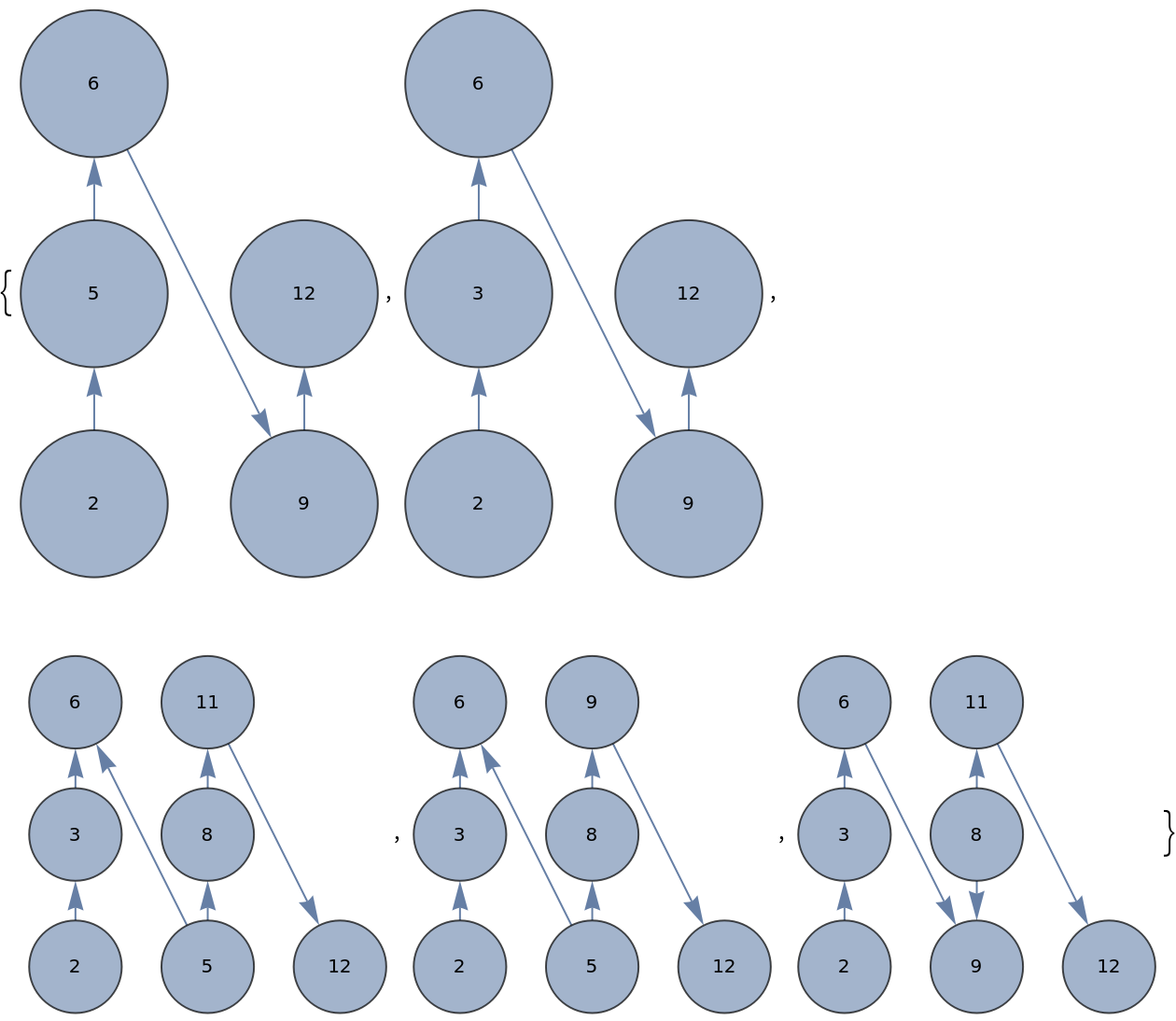
Small graphs:
Options (2)
By default, the weak path graphs created by this function inherit options from the underlying graph. One can use any option available to Graph to override those options or to add other options:
One can also choose to prevent inheritance altogether:
One can also choose to inherit only listed options:
And one can combine inheritance of listed options with additional options:
Instead of a list of options you want inherited, you can specify options you want disinherited:
Applications (3)
One can show the weak paths in the context of the original graph:
Find links between blogs that exist only when the orientation of the graph is disregarded, but show the orientation of the edges on the path:
There are no conventional paths:
There are paths if orientation is disregarded:
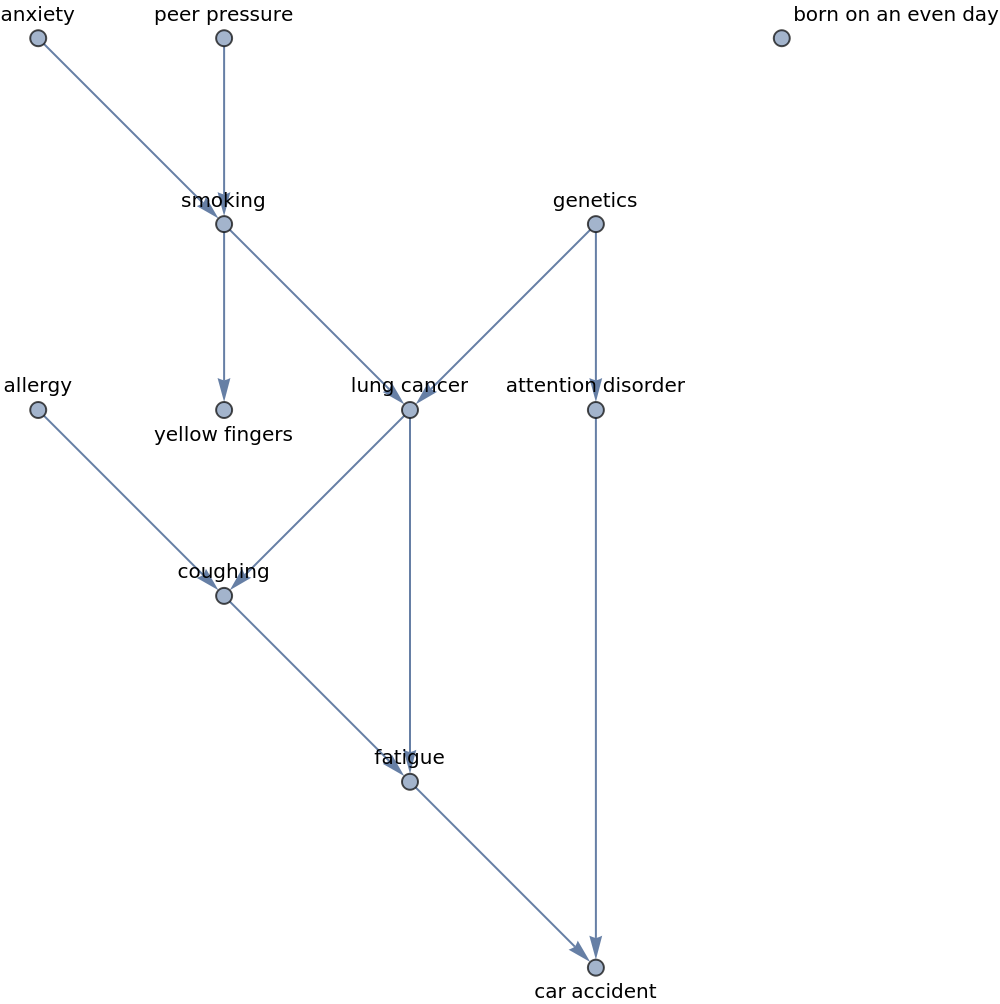
Find "backdoor" paths as well as directed paths in a causal network:
Show that deleting all incoming edges to attention disorder means that the only paths remaining between lung cancer and car accident are direct causal chains:
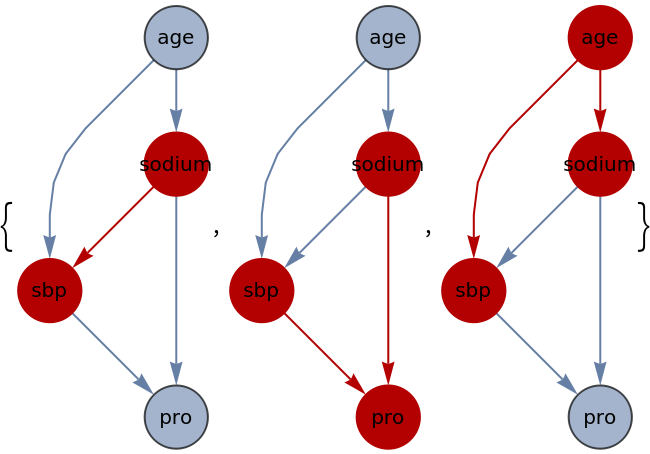
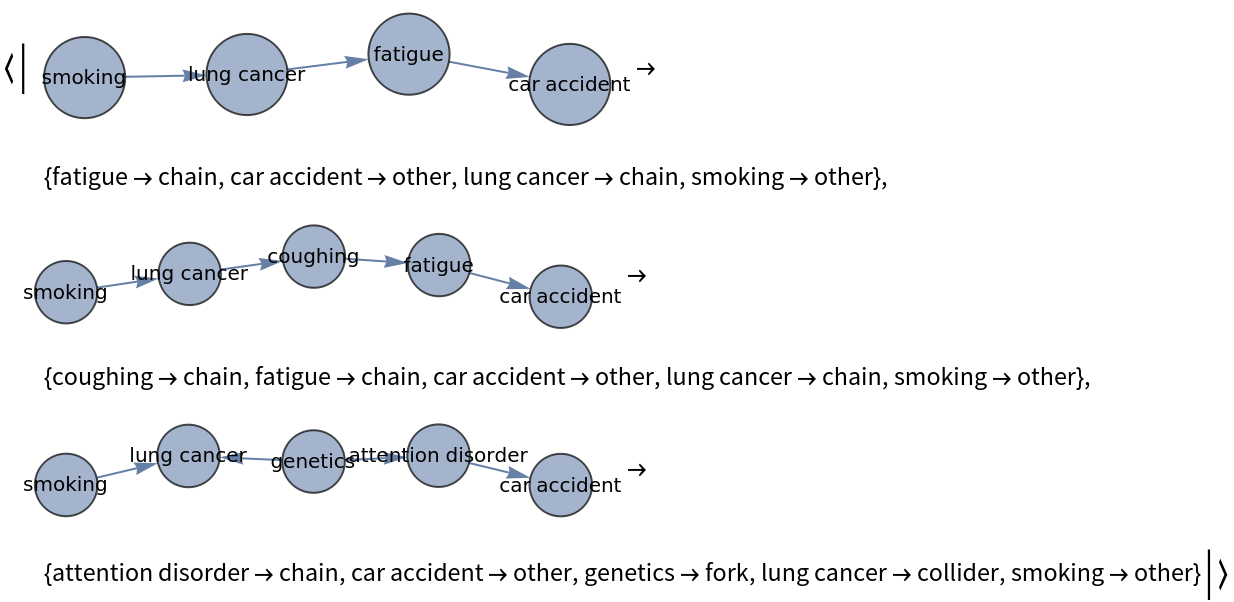
Characterize all the "triples" on direction tolerant paths between two vertices as "chains," "forks" or "colliders":
Neat Examples (1)
Determine whether two nodes of a graph are "d-separated" from each other by seeing if there are colliders on all the weak paths between two vertices:

![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, {Null,
SparseArray[
Automatic, {12, 12}, 0, {1, {{0, 2, 5, 7, 10, 14, 17, 20, 24, 27, 29, 32, 34}, {{
2}, {4}, {1}, {3}, {5}, {2}, {6}, {1}, {5}, {7}, {2}, {
4}, {6}, {8}, {3}, {5}, {9}, {4}, {8}, {10}, {5}, {7}, {
9}, {11}, {6}, {8}, {12}, {7}, {11}, {8}, {10}, {12}, {
9}, {11}}}, Pattern}]}, {GraphLayout -> {"GridEmbedding", "Dimension" -> {3, 4}}, VertexShapeFunction -> {2 -> "Name", 7 -> "Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$10", Automatic, Center]}, {
DynamicLocation[
"VertexID$8", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}, {
DynamicLocation[
"VertexID$8", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}, {
DynamicLocation[
"VertexID$9", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}, {
DynamicLocation[
"VertexID$10", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}, {
DynamicLocation[
"VertexID$11", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{1., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{2., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{2., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{2., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["7", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {3., 1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{3., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$8"],
TagBox[
DiskBox[{3., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$9"],
TagBox[
DiskBox[{4., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$10"],
TagBox[
DiskBox[{4., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$11"],
TagBox[
DiskBox[{4., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$12"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-1., 89.24835191419872}, {-35.275820010886434`, 32.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None]\), 2, 7, ImageSize -> 100, VertexLabels -> "Name"]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/13d027f8ed4a00b1.png)
![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, {Null,
SparseArray[
Automatic, {12, 12}, 0, {1, {{0, 2, 5, 7, 10, 14, 17, 20, 24, 27, 29, 32, 34}, {{
2}, {4}, {1}, {3}, {5}, {2}, {6}, {1}, {5}, {7}, {2}, {
4}, {6}, {8}, {3}, {5}, {9}, {4}, {8}, {10}, {5}, {7}, {
9}, {11}, {6}, {8}, {12}, {7}, {11}, {8}, {10}, {12}, {
9}, {11}}}, Pattern}]}, {GraphLayout -> {"GridEmbedding", "Dimension" -> {3, 4}}, VertexShapeFunction -> {2 -> "Name", 7 -> "Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
LineBox[{{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}, {
DynamicLocation[
"VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}, {
DynamicLocation[
"VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}, {
DynamicLocation[
"VertexID$4", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}, {
DynamicLocation[
"VertexID$5", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$6", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}, {
DynamicLocation[
"VertexID$7", Automatic, Center],
DynamicLocation["VertexID$10", Automatic, Center]}, {
DynamicLocation[
"VertexID$8", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}, {
DynamicLocation[
"VertexID$8", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}, {
DynamicLocation[
"VertexID$9", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}, {
DynamicLocation[
"VertexID$10", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}, {
DynamicLocation[
"VertexID$11", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{1., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{2., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{2., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{2., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["7", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {3., 1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{3., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$8"],
TagBox[
DiskBox[{3., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$9"],
TagBox[
DiskBox[{4., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$10"],
TagBox[
DiskBox[{4., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$11"],
TagBox[
DiskBox[{4., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$12"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-1., 89.24835191419872}, {-35.275820010886434`, 32.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None]\), 2, 7, ImageSize -> 100, VertexLabels -> "Name", GraphLayout -> "SpringEmbedding", "Disinherit" -> VertexShapeFunction]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/7c47f88781c4b253.png)

![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, {
SparseArray[
Automatic, {12, 12}, 0, {1, {{0, 2, 4, 5, 7, 9, 10, 12, 14, 15, 16, 17, 17}, {{
2}, {4}, {3}, {5}, {6}, {5}, {7}, {6}, {8}, {9}, {8}, {
10}, {9}, {11}, {12}, {11}, {12}}}, Pattern}], Null}, {EdgeStyle -> {
Arrowheads[0.08]}, GraphLayout -> {"GridEmbedding", "Dimension" -> {3, 4}}, VertexShapeFunction -> {2 -> "Name", 12 -> "Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.028937842778793414`],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$6", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$10", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$9", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$10", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False],
StyleBox[
ArrowBox[
LineBox[{
DynamicLocation["VertexID$11", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}]],
Arrowheads[0.08], StripOnInput -> False]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
DiskBox[{1., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{2., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{2., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{2., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
DiskBox[{3., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{3., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$8"],
TagBox[
DiskBox[{3., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$9"],
TagBox[
DiskBox[{4., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$10"],
TagBox[
DiskBox[{4., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$11"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["12", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {4., 3.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$12"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-1.015368312707917, 91.01536831270788}, {-35.1958952588157, 28.44432240452428}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None]\), 2, 12, {1, 6}, 5, ImageSize -> 200, VertexSize -> 0.7, VertexLabels -> Placed[Automatic, Center], "Disinherit" -> VertexShapeFunction]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/56b69c12e62664e8.png)
![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, {Null, {{1, 2}, {1, 4}, {2, 3}, {2, 5}, {3, 6}, {4, 5}, {
4, 7}, {5, 6}, {5, 8}, {6, 9}, {7, 8}, {7, 10}, {8, 9}, {8, 11}, {9, 12}, {10, 11}, {11, 12}, {5, 8}}}, {PerformanceGoal -> "Q", VertexCoordinates -> {{1., 1.}, {1., 2.}, {1., 3.}, {2., 1.}, {2., 2.}, {2., 3.}, {3., 1.}, {3., 2.}, {3., 3.}, {4., 1.}, {4., 2.}, {4., 3.}}, VertexShapeFunction -> {2 -> "Name", 7 -> "Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]], FontFamily -> "Arial",
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$5", Automatic, Center], {
2.5000000000000004`, 2.1378065801163424`},
DynamicLocation["VertexID$8", Automatic, Center]}],
BezierCurveBox[{
DynamicLocation["VertexID$5", Automatic, Center], {
2.5000000000000004`, 1.862193419883658},
DynamicLocation["VertexID$8", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$6", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$10", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$9", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$10", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$11", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]], FontFamily -> "Arial",
TagBox[
DiskBox[{1., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{2., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{2., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{2., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["7", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {3., 1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{3., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$8"],
TagBox[
DiskBox[{3., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$9"],
TagBox[
DiskBox[{4., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$10"],
TagBox[
DiskBox[{4., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$11"],
TagBox[
DiskBox[{4., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$12"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-1., 89.24835191419872}, {-35.275820010886434`, 32.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
BaseStyle->(FontFamily -> "Arial"),
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]],
LabelStyle->{FontFamily -> "Arial"}]\), 2, 7, {3, 4}, 2, VertexSize -> 0.5, VertexLabels -> Placed[Automatic, Center], "Disinherit" -> VertexShapeFunction]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/56bd15b34ea25832.png)
![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, {{{5, 8}}, {{1, 2}, {1, 4}, {2, 3}, {2, 5}, {3, 6}, {4, 5}, {4, 7}, {5, 6}, {6, 9}, {7, 8}, {7, 10}, {8, 9}, {8, 11}, {9, 12}, {10, 11}, {11, 12}}}, {EdgeStyle -> {
Arrowheads[0.08]}, PerformanceGoal -> "Q", VertexCoordinates -> {{1., 1.}, {1., 2.}, {1., 3.}, {2., 1.}, {2., 2.}, {2., 3.}, {3., 1.}, {3., 2.}, {3., 3.}, {4., 1.}, {4., 2.}, {4., 3.}}, VertexShapeFunction -> {2 -> "Name", 7 -> "Name"}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Arrowheads[0.028937842778793414`],
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]], FontFamily -> "Arial",
Arrowheads[0.08],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$5", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$4", Automatic, Center],
DynamicLocation["VertexID$7", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$6", Automatic, Center]}],
ArrowBox[{
DynamicLocation["VertexID$5", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$6", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$8", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$7", Automatic, Center],
DynamicLocation["VertexID$10", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$9", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$8", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$9", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$10", Automatic, Center],
DynamicLocation["VertexID$11", Automatic, Center]}],
LineBox[{
DynamicLocation["VertexID$11", Automatic, Center],
DynamicLocation["VertexID$12", Automatic, Center]}]}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]], FontFamily -> "Arial",
TagBox[
DiskBox[{1., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1., 2.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
DiskBox[{1., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
DiskBox[{2., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$4"],
TagBox[
DiskBox[{2., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$5"],
TagBox[
DiskBox[{2., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$6"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["7", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {3., 1.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$7"],
TagBox[
DiskBox[{3., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$8"],
TagBox[
DiskBox[{3., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$9"],
TagBox[
DiskBox[{4., 1.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$10"],
TagBox[
DiskBox[{4., 2.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$11"],
TagBox[
DiskBox[{4., 3.}, 0.030239520958083826`], "DynamicName", BoxID -> "VertexID$12"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{-1., 89.24835191419872}, {-35.275820010886434`, 32.}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
BaseStyle->(FontFamily -> "Arial"),
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]],
LabelStyle->{FontFamily -> "Arial"}]\), 2, 7, {1, \[Infinity]}, 1, VertexSize -> 0.5, VertexLabels -> Placed[Automatic, Center]]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/370ddfb4ef25fdc4.png)
![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4}, {Null,
SparseArray[
Automatic, {4, 4}, 0, {1, {{0, 3, 5, 8, 10}, {{2}, {3}, {4}, {1}, {3}, {1}, {
2}, {4}, {1}, {3}}}, Pattern}]}, {EdgeLabels -> {"EdgeWeight"}, VertexShapeFunction -> {"Name"}, EdgeWeight -> {0.5, 1.2, 0.2, 0.9, 0.62}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]], {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$1"],
InsetBox[
FormBox["\"0.5\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$1", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$2"],
InsetBox[
FormBox["\"1.2\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$2", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$3"],
InsetBox[
FormBox["\"0.2\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$3", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$4"],
InsetBox[
FormBox["\"0.9\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$4", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$5"],
InsetBox[
FormBox["\"0.62\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$5", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9329038775049628, 0.868997056961016}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 0.4347904415891483}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9339517502051011, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.8680693714551628`, 0.43527754789663736`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{12.122578125, 124.00632812500001`}, {-35.932423961161355`, 30.462325}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImagePadding->15,
ImageSize->{136.12890625, Automatic}]\), 2, 4]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/1efbda7e31fc3a14.png)
![ResourceFunction["WeakPathGraphs"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4}, {Null,
SparseArray[
Automatic, {4, 4}, 0, {1, {{0, 3, 5, 8, 10}, {{2}, {3}, {4}, {1}, {3}, {1}, {
2}, {4}, {1}, {3}}}, Pattern}]}, {EdgeLabels -> {"EdgeWeight"}, VertexShapeFunction -> {"Name"}, EdgeWeight -> {0.5, 1.2, 0.2, 0.9, 0.62}}]], Typeset`boxes, Typeset`boxes$s2d = GraphicsGroupBox[{{
Directive[
Opacity[0.7],
Hue[0.6, 0.7, 0.5]], {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$2", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$1"],
InsetBox[
FormBox["\"0.5\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$1", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$2"],
InsetBox[
FormBox["\"1.2\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$2", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$1", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$3"],
InsetBox[
FormBox["\"0.2\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$3", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$2", Automatic, Center],
DynamicLocation["VertexID$3", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$4"],
InsetBox[
FormBox["\"0.9\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$4", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}, {
TagBox[
LineBox[{
DynamicLocation["VertexID$3", Automatic, Center],
DynamicLocation["VertexID$4", Automatic, Center]}], "DynamicName", BoxID -> "EdgeLabelID$5"],
InsetBox[
FormBox["\"0.62\"", TraditionalForm],
Offset[{0, 2},
DynamicLocation["EdgeLabelID$5", Automatic,
Scaled[0.5]]], {0, -1}, BaseStyle -> "Graphics"]}}, {
Directive[
Hue[0.6, 0.2, 0.8],
EdgeForm[
Directive[
GrayLevel[0],
Opacity[0.7]]]],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["1", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9329038775049628, 0.868997056961016}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$1"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["2", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0., 0.4347904415891483}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$2"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["3", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {0.9339517502051011, 0.}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$3"],
TagBox[
InsetBox[
BoxData[
FormBox[
PaneBox["4", Alignment -> Center, ImageMargins -> 2], TraditionalForm]], {1.8680693714551628`, 0.43527754789663736`}, BaseStyle -> "Graphics"], "DynamicName", BoxID -> "VertexID$4"]}}], $CellContext`flag},
TagBox[
DynamicBox[GraphComputation`NetworkGraphicsBox[
3, Typeset`graph, Typeset`boxes, $CellContext`flag], {CachedValue :> Typeset`boxes, SingleEvaluation -> True, SynchronousUpdating -> False, TrackedSymbols :> {$CellContext`flag}},
ImageSizeCache->{{12.122578125, 124.00632812500001`}, {-35.932423961161355`, 30.462325}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False,
UnsavedVariables:>{$CellContext`flag}]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
ImagePadding->15,
ImageSize->{136.12890625, Automatic}]\), 2, 4, "Disinherit" -> {EdgeWeight}]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/601294792e677e62.png)
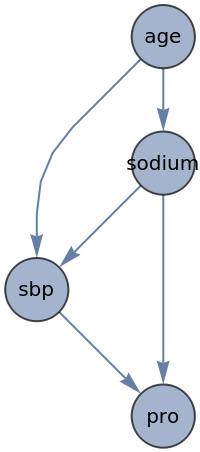
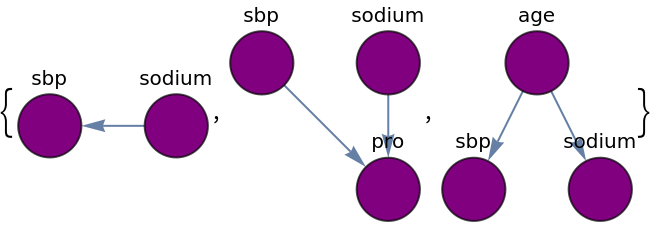
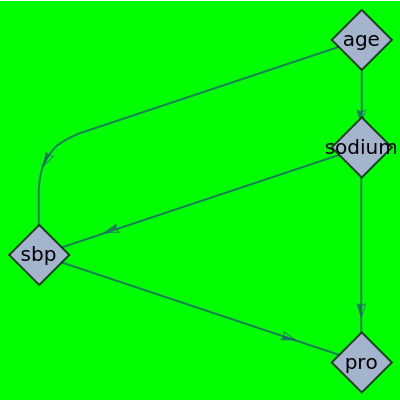
![gr = Graph[{"sodium" -> "sbp", "age" -> "sodium", "age" -> "sbp", "sodium" -> "pro", "sbp" -> "pro"}, VertexLabels -> Placed["Name", Center], EdgeShapeFunction -> "CarvedArrow", VertexSize -> 0.5, VertexShapeFunction -> "Diamond", ImageSize -> 200, Background -> Green, AspectRatio -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/749cb265ec890c1f.png)
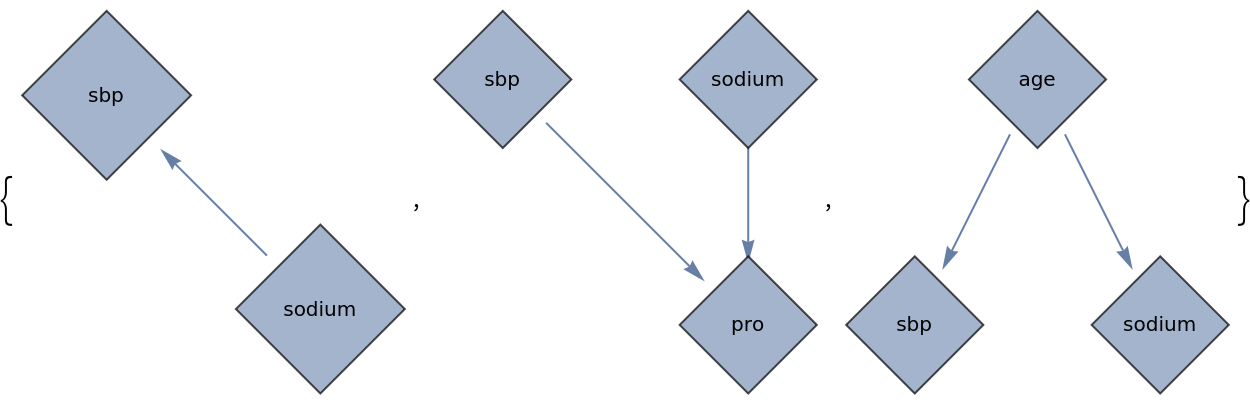
![With[{g = Graph[{"sodium" -> "sbp", "age" -> "sodium", "age" -> "sbp", "sodium" -> "pro", "sbp" -> "pro"}, VertexLabels -> Placed["Name", Center], VertexSize -> 0.5, ImageSize -> 100]}, Map[HighlightGraph[g, #] &, ResourceFunction["WeakPathGraphs"][g, "sodium", "sbp", {1, \[Infinity]}, All]]]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/406571c37a531466.png)
![ResourceFunction[
"WeakPathGraphs"][blogs, "talkingpointsmemo.com", "realclearpolitics.com", {1, 3}, 1, VertexLabels -> Placed["Name", Center], VertexLabelStyle -> Directive[Red, Italic, 8], GraphLayout -> "SpringEmbedding", ImageSize -> 600]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/0472f7d242c6a472.png)

![cancerGraph = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"anxiety", "smoking", "peer pressure", "yellow fingers", "lung cancer", "genetics", "attention disorder", "fatigue", "coughing", "allergy", "car accident", "born on an even day"}, {{{1, 2}, {3, 2}, {2, 4}, {2, 5}, {
6, 5}, {6, 7}, {5, 8}, {5, 9}, {10, 9}, {8, 11}, {7, 11}, {
9, 8}}, Null}, {GraphLayout -> "LayeredDigraphEmbedding", VertexLabels -> {"Name"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{0.5000100000000001, -0.5000099999999996}, {
1.50001, -1.5000099999999996`}}, 0.043048128342245986`], ArrowBox[{{1.50001, -1.5000099999999996`}, {
1.50001, -2.5000099999999996`}}, 0.043048128342245986`], ArrowBox[{{1.50001, -1.5000099999999996`}, {
2.50001, -2.5000099999999996`}}, 0.043048128342245986`], ArrowBox[{{1.50001, -0.5000099999999996}, {
1.50001, -1.5000099999999996`}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQbZmka8fKwOJgAaEPQGmHJ5NCKiQTWA7A5DskRY55
nWI5YAXlK33LVp9pxwqX36QRM4dlLytc3nrjE5VeVza4/O5+1oNGNxB8wyP7
Cr6WsMP58/0ETK5Kc8D5LPq/uC6d4YC7J8VqQ/bdJk64/DHXtDMvLLjg9qkH
yuh+eccFl2+PudT7fwk3XP5Fesc7rmgeuLxXsZ2/mCAvnL+q7st6xeMIPnfX
KgHdWj44P3tqQqGFMT/cPedLvTxMn/DD5eUZzrV2uQrA7Yueteru68kCcPnZ
nLtX291FyN/z/f++SVEQLq+RXr5qRwKCXxKqfPv+LAT/mARz04/zCL7MRrH5
TAxCBwA3bIq1
"]], 0.043048128342245986`], ArrowBox[{{2.50001, -2.5000099999999996`}, {
1.50001, -3.5000099999999996`}}, 0.043048128342245986`], ArrowBox[{{3.50001, -1.5000099999999996`}, {
2.50001, -2.5000099999999996`}}, 0.043048128342245986`], ArrowBox[{{3.50001, -1.5000099999999996`}, {
3.50001, -2.5000099999999996`}}, 0.043048128342245986`], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQbZmka8fKwONgAaZZDlhA+U8mhVRIJiD4HZIix7xO
sRyAqVf6lq0+044VLr9JI2YOy17WA1ZQvvXGJyq9rmxw+d39rAeNbrDB9Rse
2VfwtYQdzp/vJ2ByVZoDzmfR/8V16QwHXH+K1Ybsu02ccP4x17QzLyy44OrV
A2V0v7zjgsu3x1zq/b+EG+6eF+kd77iieeDyXsV2/mKCvHD9q+q+rFc8juBz
d60S0K3lg/ObxGtZM9ME4PoNZW9szTuI4D9WMk4rkRGEq5+i0SdWVS4Il3fR
e3ms/pIg3D1fjF3KW3WF4PJLLeerd3cIwfWH2v+6PuExgs/qGtoxzU4Yzt/m
tcFizkxhuP4XVqpLpD4h+AoM51q7XEXg6mNmrbr7erIIXH4W5+7VdndF4O65
5/v/fZOiKFxeI7181Y4EUbj+klDl2/dnIfjHJJibfpxH8GU2is1nYhA7AACW
DLgP
"]], 0.043048128342245986`], ArrowBox[{{2.50001, -4.50001}, {3.50001, -5.50001}}, 0.043048128342245986`], ArrowBox[{{1.50001, -3.5000099999999996`}, {
2.50001, -4.50001}}, 0.043048128342245986`], ArrowBox[{{0.5000100000000001, -2.5000099999999996`}, {
1.50001, -3.5000099999999996`}}, 0.043048128342245986`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{0.5000100000000001, -0.5000099999999996}, 0.043048128342245986], InsetBox["\<\"anxiety\"\>", Offset[{0, 2}, {0.5000100000000001, -0.45696187165775365}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.50001, -1.5000099999999996}, 0.043048128342245986], InsetBox["\<\"smoking\"\>", Offset[{0, 2}, {1.50001, -1.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.50001, -0.5000099999999996}, 0.043048128342245986], InsetBox["\<\"peer pressure\"\>", Offset[{0, 2}, {1.50001, -0.45696187165775365}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.50001, -2.5000099999999996}, 0.043048128342245986], InsetBox["\<\"yellow fingers\"\>", Offset[{0, -2}, {1.50001, -2.5430581283422455}], ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.50001, -2.5000099999999996}, 0.043048128342245986], InsetBox["\<\"lung cancer\"\>", Offset[{0, 2}, {2.50001, -2.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.50001, -1.5000099999999996}, 0.043048128342245986], InsetBox["\<\"genetics\"\>", Offset[{0, 2}, {3.50001, -1.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.50001, -2.5000099999999996}, 0.043048128342245986], InsetBox["\<\"attention disorder\"\>", Offset[{0, 2}, {3.50001, -2.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.50001, -4.50001}, 0.043048128342245986], InsetBox["\<\"fatigue\"\>", Offset[{0, 2}, {2.50001, -4.456961871657754}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.50001, -3.5000099999999996}, 0.043048128342245986], InsetBox["\<\"coughing\"\>", Offset[{0, 2}, {1.50001, -3.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.5000100000000001, -2.5000099999999996}, 0.043048128342245986], InsetBox["\<\"allergy\"\>", Offset[{0, 2}, {0.5000100000000001, -2.4569618716577537}], ImageScaled[{0.5, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{3.50001, -5.50001}, 0.043048128342245986], InsetBox["\<\"car accident\"\>", Offset[{0, -2}, {3.50001, -5.5430581283422455}], ImageScaled[{0.5, 1}],
BaseStyle->"Graphics"]}, {
DiskBox[{4.500030000000001, -0.50001}, 0.043048128342245986], InsetBox["\<\"born on an even day\"\>", Offset[{2, 2}, {4.543078128342247, -0.456961871657754}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{672.59375, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/6f98e4a64282b1e2.png)
![ResourceFunction["WeakPathGraphs"][cancerGraph, "lung cancer", "car accident", VertexLabels -> Placed["Name", Center], GraphLayout -> "SpringEmbedding", ImageSize -> 300, VertexSize -> 0.5] // Column](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/7028bd4e6b260e25.png)
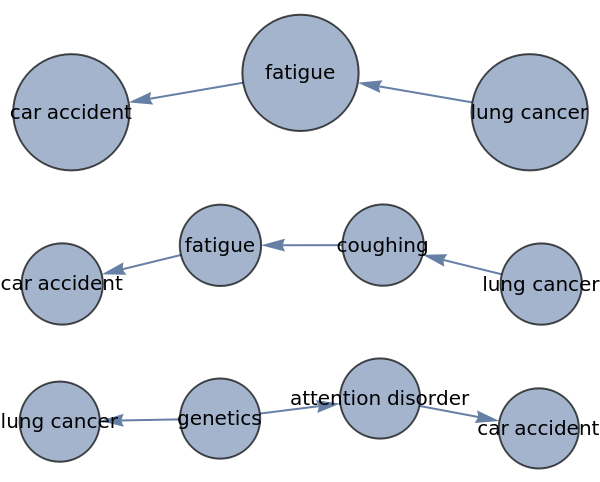
![ResourceFunction["WeakPathGraphs"][
EdgeDelete[
cancerGraph, _ \[DirectedEdge] "attention disorder"], "lung cancer", "car accident", VertexLabels -> Placed["Name", Center], GraphLayout -> "SpringEmbedding", ImageSize -> 300, VertexSize -> 0.5]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/48908e4896fa131a.png)

![tripleType[gr_Graph] := Map[#[[1]] -> Switch[Rest[#], {1, 1}, "chain", {0, 2}, "fork", {2, 0}, "collider", _, "other"] &, Thread[List[VertexList[gr], VertexInDegree[gr], VertexOutDegree[gr]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/76816e1906b2ef82.png)
![AssociationMap[tripleType, ResourceFunction["WeakPathGraphs"][cancerGraph, "smoking", "car accident", VertexLabels -> Placed["Name", Center], GraphLayout -> "SpringEmbedding", ImageSize -> 300, VertexSize -> 0.5]]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/4ab6565fde3174aa.png)
![cancerGraph = Graph[{"anxiety", "smoking", "peer pressure", "yellow fingers", "lung cancer", "genetics", "attention disorder", "fatigue", "coughing", "allergy", "car accident", "born on an even day"}, {"anxiety" \[DirectedEdge] "smoking", "peer pressure" \[DirectedEdge] "smoking", "smoking" \[DirectedEdge] "yellow fingers", "smoking" \[DirectedEdge] "lung cancer", "genetics" \[DirectedEdge] "lung cancer", "genetics" \[DirectedEdge] "attention disorder", "lung cancer" \[DirectedEdge] "fatigue", "lung cancer" \[DirectedEdge] "coughing", "allergy" \[DirectedEdge] "coughing", "fatigue" \[DirectedEdge] "car accident", "attention disorder" \[DirectedEdge] "car accident", "coughing" \[DirectedEdge] "fatigue"}, VertexLabels -> "Name", GraphLayout -> "LayeredDigraphEmbedding", ImageSize -> 500]](https://www.wolframcloud.com/obj/resourcesystem/images/120/1206d30b-3007-45d2-bb72-c368c6c86548/757d52915a5889c3.png)