Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VoronoiCellTours

Source Notebook

Compute shortest tours visiting all lattice points within each Voronoi cell in a region

Contributed by: Shiv Kampani

ResourceFunction["VoronoiCellTours"][pts, reg]

computes shortest tours starting from each point in pts within each Voronoi cell of the Voronoi diagram from pts within the region reg.

Details

A Voronoi diagram is generated within reg from pts such that each Voronoi cell contains exactly one point from pts. The shortest tour visiting all lattice points within a given Voronoi cell is computed for all Voronoi cells in the generated Voronoi diagram.
Points in pts are considered starting points for each of the shortest tours computed. Shortest tours start and end at the same point.
Lattice points that lie on the edges of a Voronoi cell are also considered to be within that cell and are included in the shortest tour.
ResourceFunction["VoronoiCellTours"] is similar to the procedure used in this Wolfram Community post. The tours computed by ResourceFunction["VoronoiCellTours"] are shorter and more efficient than the paths computed in that post. This is because ResourceFunction["VoronoiCellTours"] takes the region as a parameter whereas the Community post does not.
The method used in this Wolfram Community post represents the optimum method of exploring an unknown region and ResourceFunction["VoronoiCellTours"] represents the optimum method of exploring a known region.

Examples

Basic Examples (1) 

Compute shortest tours starting at three random starting points within a rectangle:

In[1]:=
SeedRandom[50]; pts = RandomInteger[{-8, 8}, {3, 2}]; reg = Rectangle[{-10, -10}, {10, 10}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; ListLinePlot[tours, ImageSize -> Medium]
Out[5]=

Scope (2) 

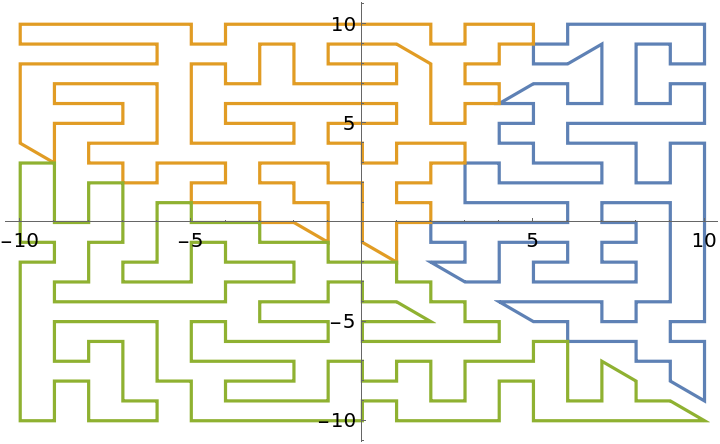Compute the shortest tour from a single point within a rectangle:

In[6]:=
pts = {{0, 0}}; reg = Rectangle[{-10, -10}, {10, 10}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; ListLinePlot[tours, ImageSize -> Medium]
Out[9]=

Compute shortest tours within Voronoi cells from five random points within a random convex polygon:

In[10]:=
SeedRandom[50]; pts = RandomInteger[{-10, 10}, {5, 2}]; reg = RandomPolygon["Convex", DataRange -> {{-20, 20}, {-20, 20}}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; ListLinePlot[tours, ImageSize -> Medium]
Out[14]=

Applications (1) 

Use the resource function LloydAlgorithm with VoronoiCellTours for shortest tours within Voronoi cells of similar areas:

In[15]:=
SeedRandom[50]; pts = RandomInteger[{-10, 10}, {5, 2}]; reg = RandomPolygon["Convex", DataRange -> {{-20, 20}, {-20, 20}}]; lloydPts = ResourceFunction["LloydAlgorithm"][pts, reg, 100]; tours = ResourceFunction["VoronoiCellTours"][lloydPts, reg]; ListLinePlot[tours, ImageSize -> Medium]
Out[20]=

Possible Issues (2) 

If a point does not lie within the region, a shortest tour is not computed within the point's Voronoi cell:

In[21]:=
pts = {{0, 0}, {11, 11}}; reg = Rectangle[{-10, -10}, {10, 10}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; ListLinePlot[tours, ImageSize -> Medium]
Out[24]=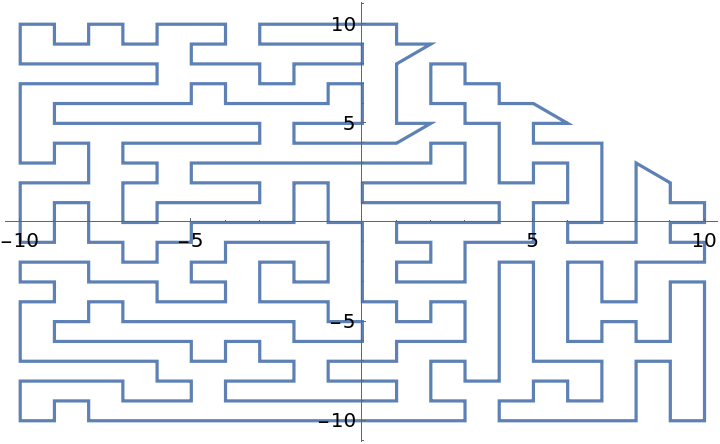

VoronoiCellTours is not able to correctly compute shortest tours for some concave regions:

In[25]:=
SeedRandom[50]; pts = {{-5, 0}, {5, 0}, {0, -5}}; reg = RandomPolygon["Simple", DataRange -> {{-20, 20}, {-20, 20}}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; Show[ListLinePlot[tours, AspectRatio -> 1], Graphics[{FaceForm[], EdgeForm[Black], reg}], PlotRange -> All, ImageSize -> Medium]
Out[29]=

Neat Examples (2) 

Compute shortest tours within Voronoi cells from eight random points within a convex polygon:

In[30]:=
SeedRandom[50]; pts = RandomInteger[{-20, 20}, {8, 2}]; reg = RandomPolygon["Convex", DataRange -> {{-50, 50}, {-50, 50}}]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; Show[ListLinePlot[tours, AspectRatio -> 1], Graphics[{FaceForm[], EdgeForm[Black], reg}], PlotRange -> All, ImageSize -> Large]
Out[34]=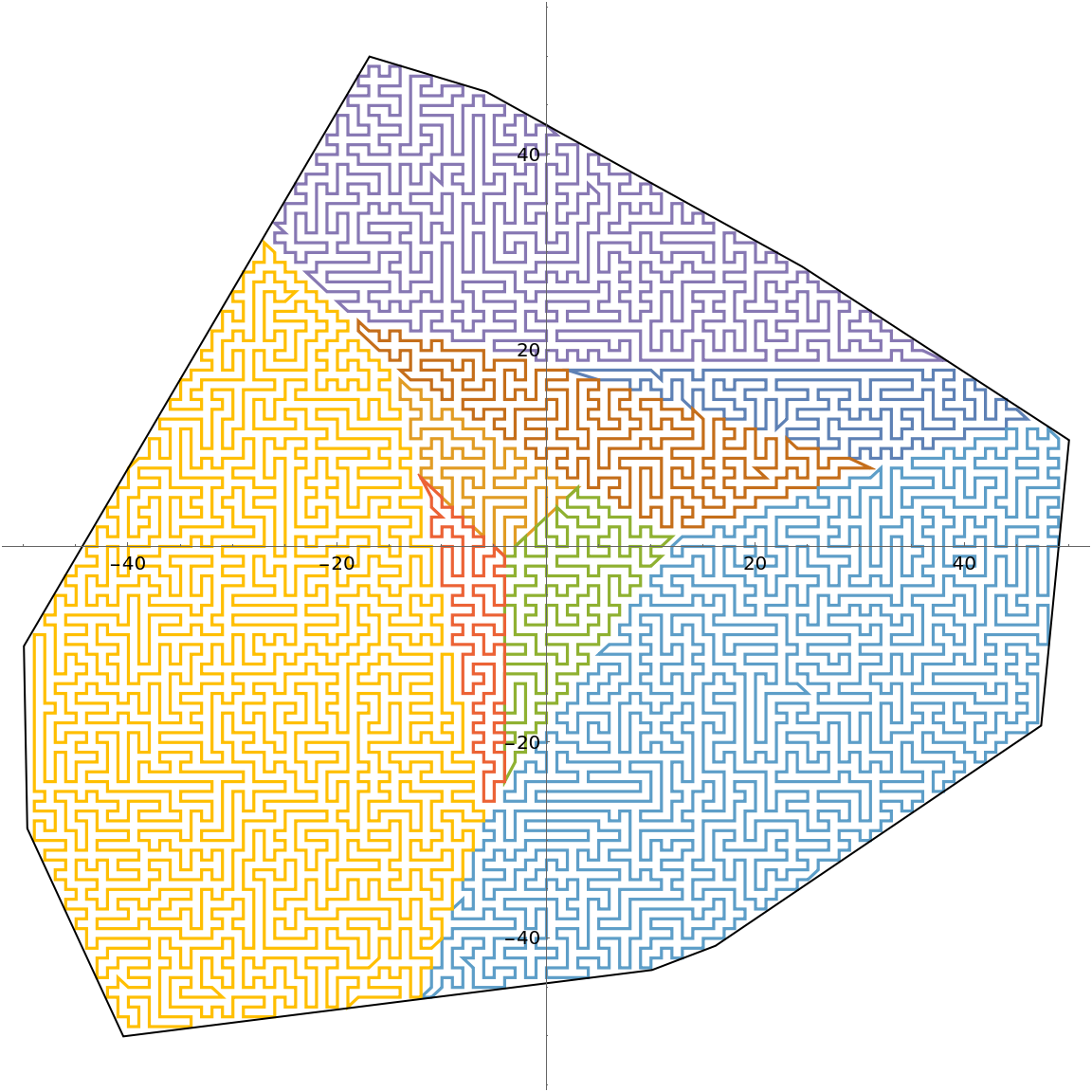

Compute shortest tours within Voronoi cells from 10 random points within a large disk region:

In[35]:=
SeedRandom[50]; pts = RandomInteger[{-40, 40}, {10, 2}]; reg = Disk[{0, 0}, 50]; tours = ResourceFunction["VoronoiCellTours"][pts, reg]; Show[ListLinePlot[tours, AspectRatio -> 1], Graphics[{FaceForm[], EdgeForm[Black], reg}], PlotRange -> All, ImageSize -> Large]
Out[39]=

Publisher

Shiv Kampani

Version History

  • 1.0.0 – 23 August 2021

Related Resources

License Information