Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VisualizeDigitPath

Source Notebook

Get a graph of the sequential digit path of a number

Contributed by: Jordan Hasler, Nicholas Brunk and the Wolfram|Alpha Math Team

ResourceFunction["VisualizeDigitPath"][n,len]

yields a graph of the sequential digit path of the number n including exactly len digits.

ResourceFunction["VisualizeDigitPath"][{n,b},len]

yields a graph of the sequential digit path in base b.

ResourceFunction["VisualizeDigitPath"][{n,base},len,type]

returns the resulting visualization specified by type.

Details

The edge weight is displayed in the tooltip upon Mouseover.
The option type defaults to "Multigraph". Specified types can also include "WeightedGraph" or "MatrixPlot".

Examples

Basic Examples (2) 

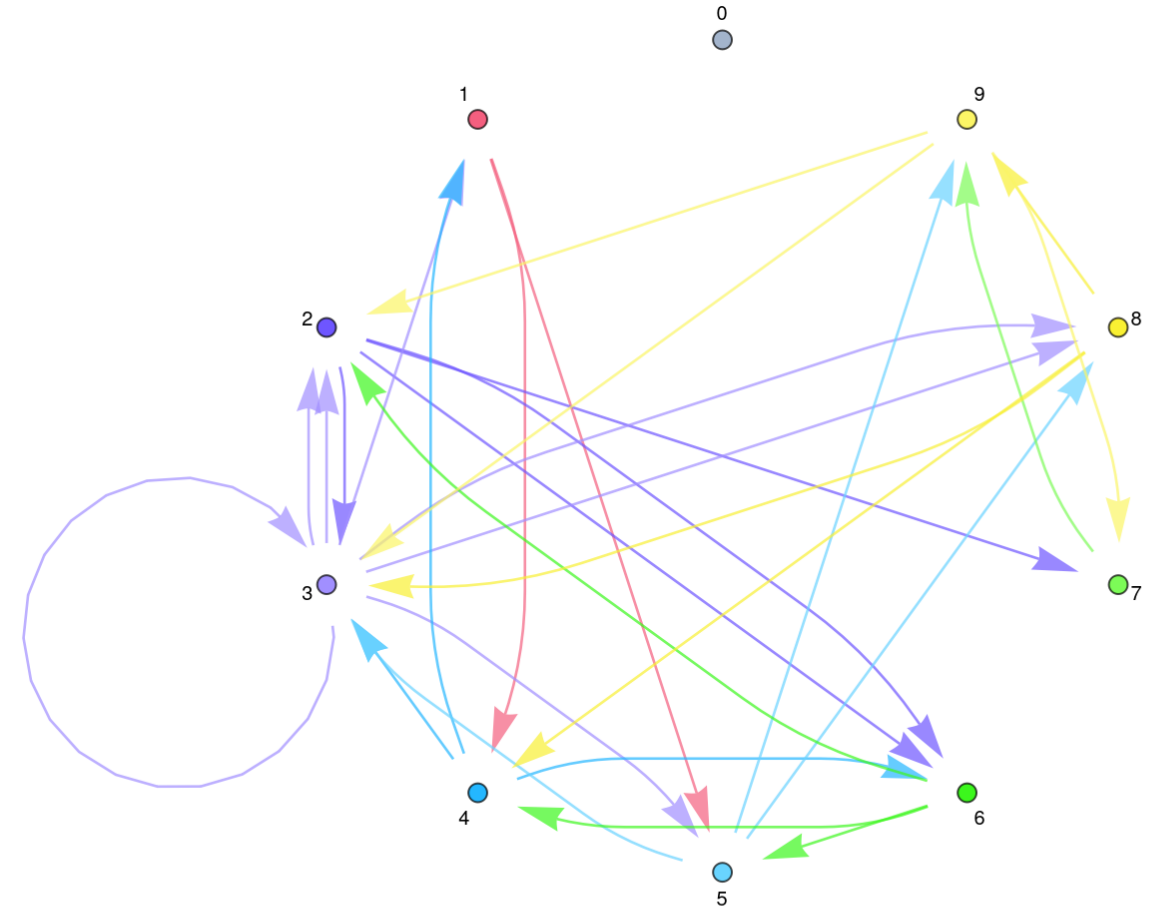
Return a Graph of the digits of Pi up to the first 30 digits:

In[1]:=
ResourceFunction["VisualizeDigitPath"][Pi, 30]
Out[1]=

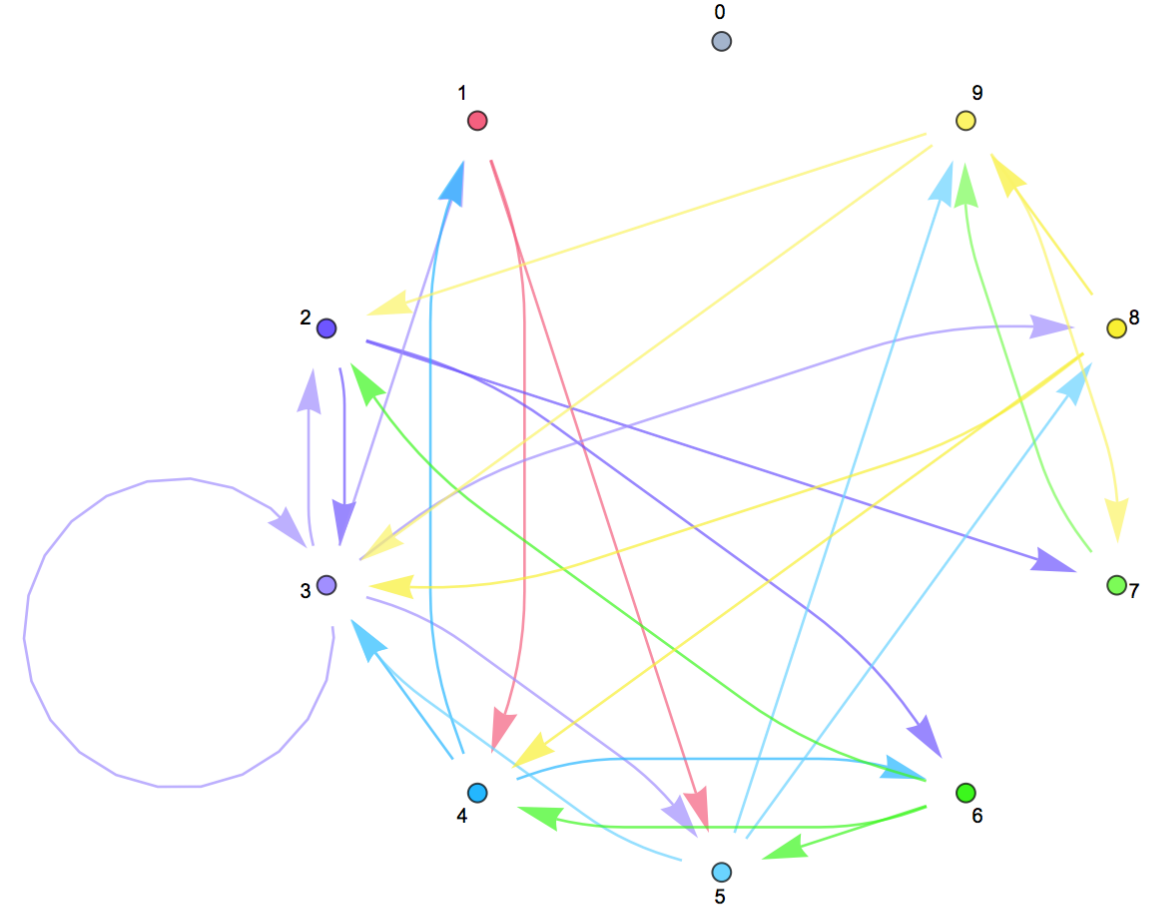
Return a weighted Graph of the digits of Pi up to the first 30 digits:

In[2]:=
ResourceFunction["VisualizeDigitPath"][Pi, 30, "WeightedGraph"]
Out[2]=

Scope (2) 

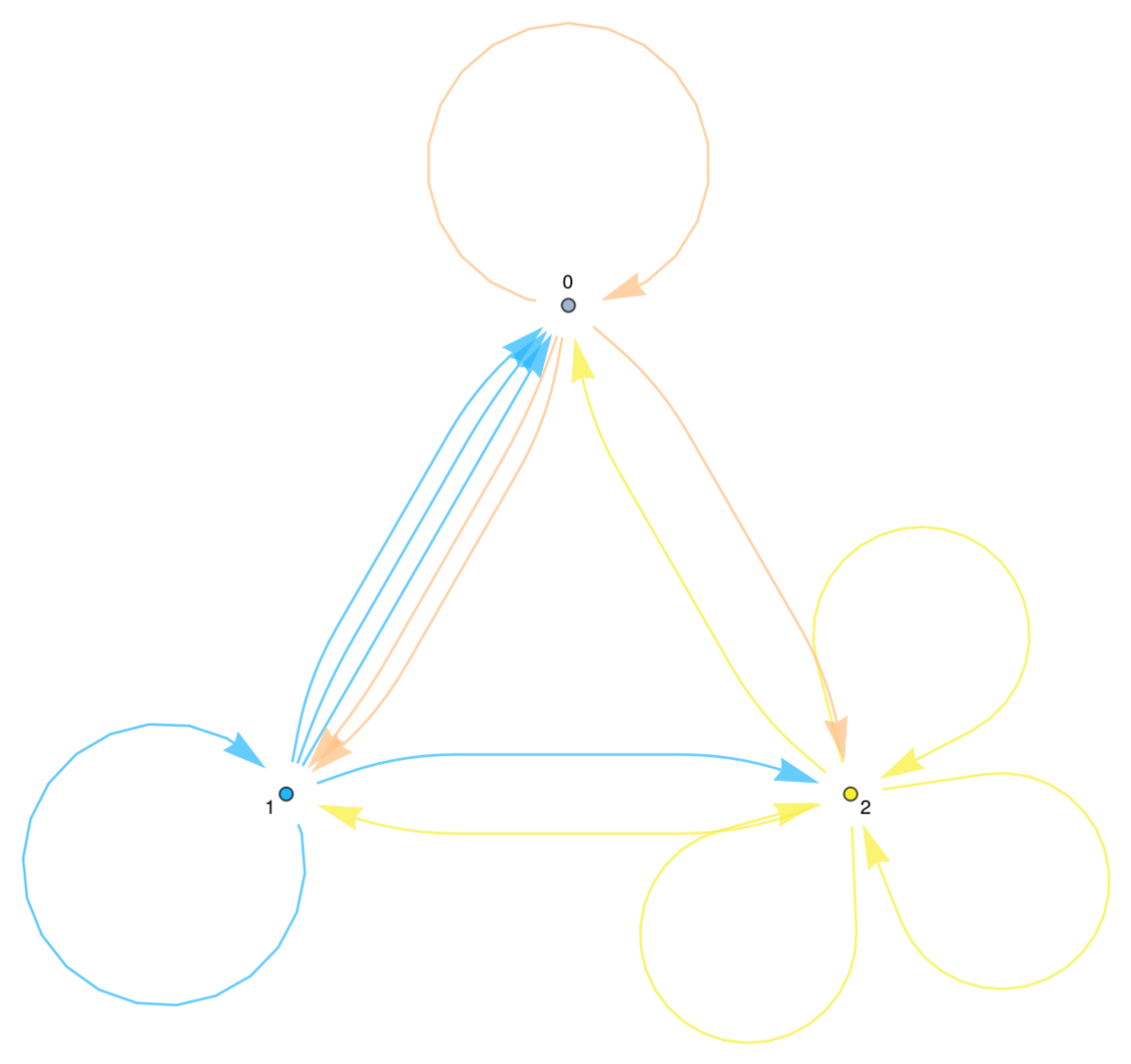
Return a Graph of the digits of Pi in base 3 up to the first 15 digits:

In[3]:=
ResourceFunction["VisualizeDigitPath"][{Pi, 3}, 15]
Out[3]=

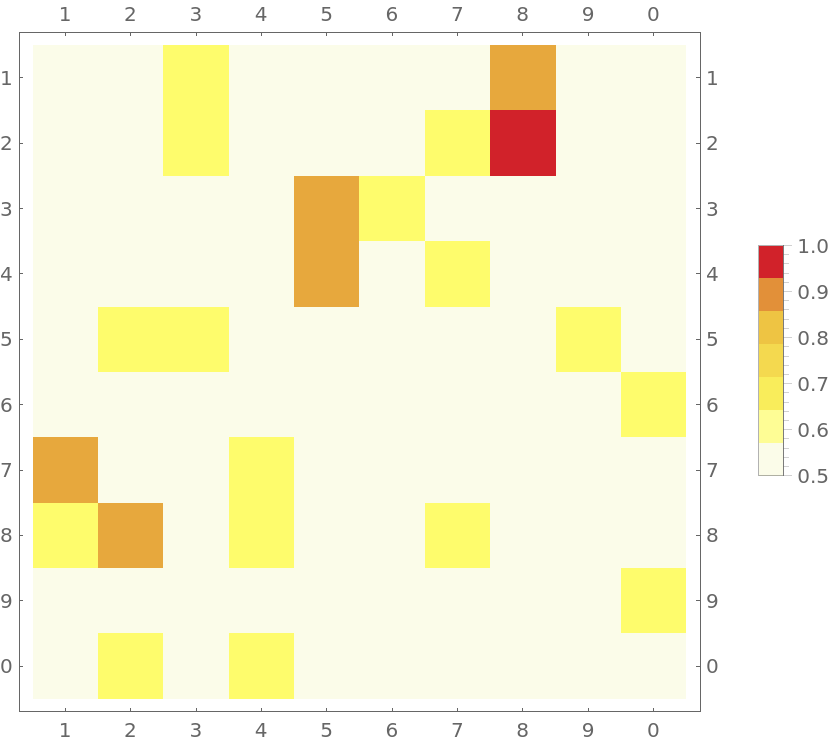
Return a MatrixPlot of the digits of E up to the first 30 digits, displaying the relative frequencies of the transitions:

In[4]:=
ResourceFunction["VisualizeDigitPath"][E, 30, "MatrixPlot"]
Out[4]=

Neat Examples (1) 

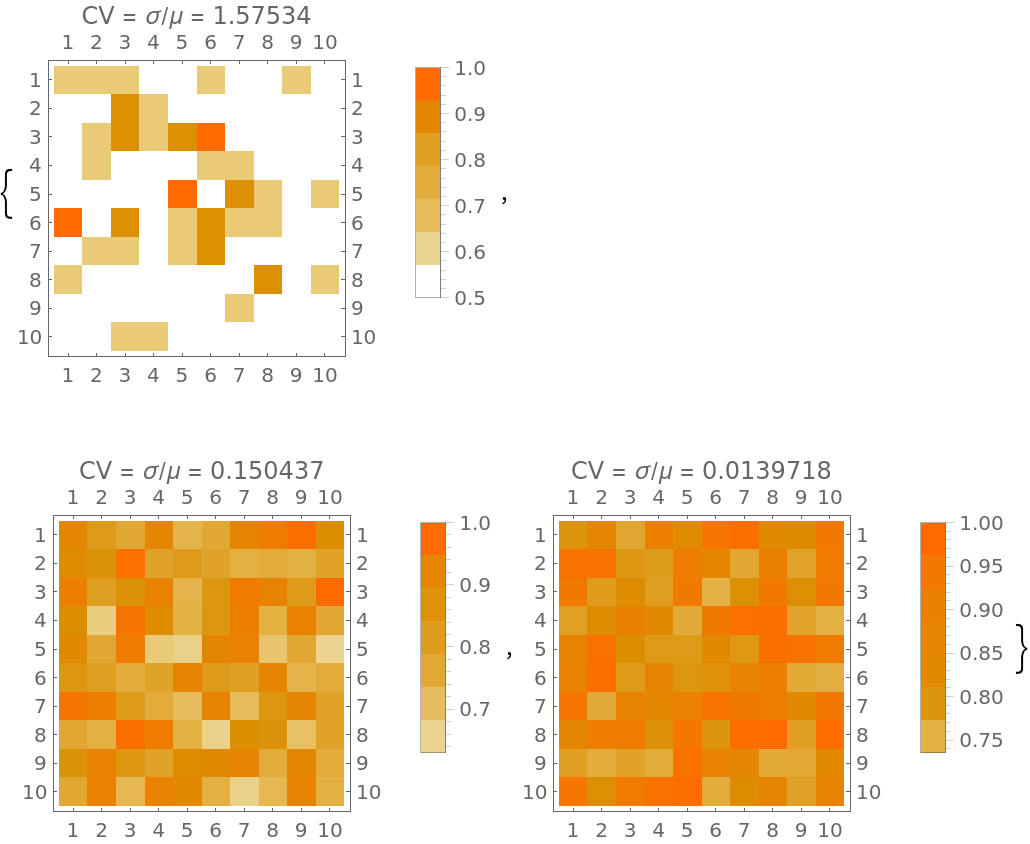
For a pseudorandom number, as you acquire more samples, the coefficient of variation scales to zero as , implying that the number is normal:

In[5]:=
Table[With[{g = WeightedAdjacencyMatrix[ ResourceFunction["VisualizeDigitPath"][ RandomReal[1, "WorkingPrecision" -> n], n]]}, MatrixPlot[g/Total[g, -1], "ColorFunctionScaling" -> True, PlotLegends -> BarLegend[Automatic, 5], PlotLabel -> "CV = \[Sigma]/\[Mu] = " <> ToString[ N@StandardDeviation[Flatten@g]/Mean[Flatten@g]]]], {n, { 50, 5000, 500000}}]
Out[5]=

Publisher

Wolfram|Alpha Math Team

Version History

  • 2.0.0 – 23 March 2023
  • 1.0.0 – 01 March 2021

Related Resources

Author Notes

To view the full source code for VisualizeDigitPath, evaluate the following:

In[1]:=
SystemOpen[ FileNameJoin[{DirectoryName[FindFile["ResourceFunctionHelpers`"]], "VisualizeDigitPath.wl"}]]

License Information