Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VertexStratify

Source Notebook

Partition the vertices of a directed acyclic graph into time-ordered level sets

Contributed by: Bradley Klee

ResourceFunction["VertexStratify"][g]

returns a minimal, time-ordered partitioning of the vertices of a directed acyclic graph g.

ResourceFunction["VertexStratify"][g,n]

returns a comprehensive set of stratifications, with at most n additional levels per stratification.

ResourceFunction["VertexStratify"][g,n,max]

introduces a cutoff max, which terminates the enumeration of stratifications.

Details

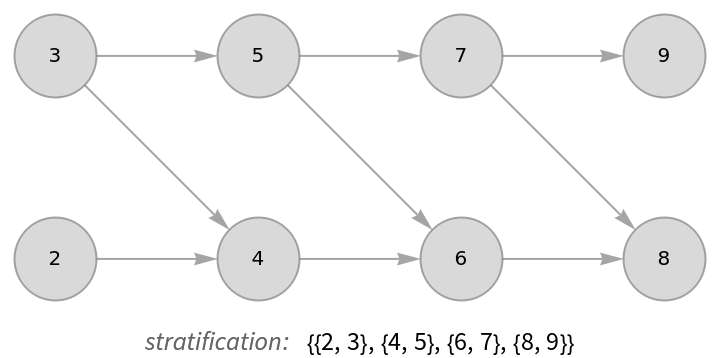
A partitioning is minimal provided each vertex appears in the level immediately after the one with its last appearing component.
Every directed acyclic graph (DAG) has a set of vertices with VertexInDegree equal to zero, called "sources"; the sources of the DAG are listed in the base level (or stratum) of the minimal stratification.
Subsequent vertices are listed in the next stratum as soon as all of their inputs are included in preceding strata. Consequently, directed edges always point from an earlier stratum to a later one.
There is an equally minimal reverse stratification obtained by applying time reversal to the input graph. Vertices with VertexOutDegree equal zero (called “sinks”) then form the base stratum. Subsequent strata membership is determined treating sinks as sources and moving reversely along directed edges.
If the forward and reverse stratifications are identical, the graph is said to be stratification-rigid.
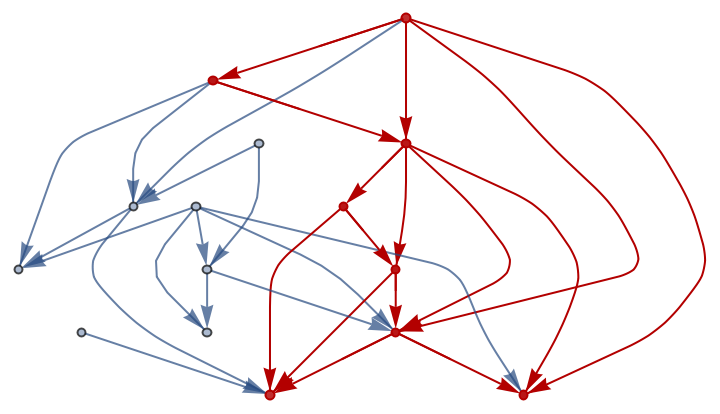
Every graph contains a stratification-rigid subgraph, which determines a stratification axis and a minimal length thereof.
If the graph is not entirely stratification-rigid, alternative stratifications can be obtained by perturbing "loose" vertices forward along the stratification axis.
Since the stratification axis has a fixed length, the number of possible stratifications must be finite.
The optional parameter n effectively lengthens the stratification axis, thus allowing enumeration of additional "extra-loose" stratifications.
Depending how large the non-stratification-rigid subgraph is, it may be necessary to introduce a cutoff max to force halting in reasonable time.

Examples

Basic Examples (3) 

Create a randomly-labeled path graph:

In[1]:=
pg = PathGraph[SeedRandom[123]; RandomSample@Range[10], DirectedEdges -> True, VertexLabels -> "Name"]
Out[1]=

Find the order of vertices:

In[2]:=
ResourceFunction["VertexStratify"][pg]
Out[2]=

Stratify vertices in a two-dimensional graph:

In[3]:=
With[{g0 = VertexDelete[DirectedGraph[GridGraph[{2, 5}], "Acyclic"], {1, 10}]}, Labeled[ Graph[g0, VertexLabels -> (x_ :> Placed[x, Center]), VertexSize -> Large, VertexStyle -> Directive[LightGray, EdgeForm[Gray]], EdgeStyle -> Gray], Row[{Style["stratification: ", GrayLevel[.4], Italic], ResourceFunction["VertexStratify"][g0]}, Spacer[2]]]]
Out[3]=

For a three-dimensional grid graph, count the number of vertices per level:

In[4]:=
With[{g0 = GridGraph[{5, 5, 5}]}, Length /@ ResourceFunction["VertexStratify"][DirectedGraph[g0, "Acyclic"]]]
Out[4]=

Scope (6) 

Plot a binary tree by using the stratification to determine vertex coordinates:

In[5]:=
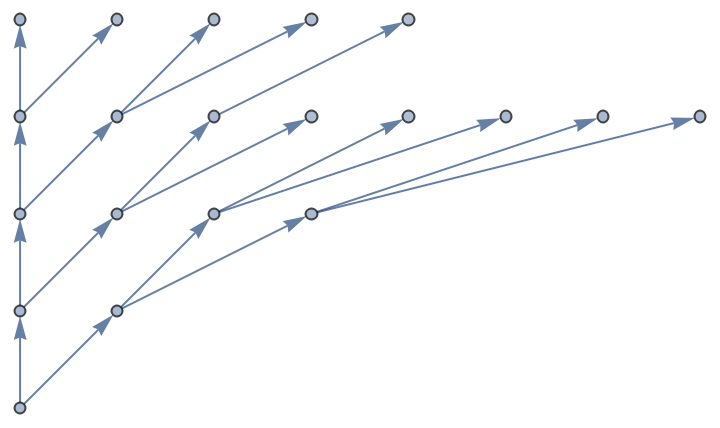
With[{g0 = KaryTree[20, 2, DirectedEdges -> True]}, Graph[EdgeList@g0, VertexCoordinates -> Flatten[ MapIndexed[#1 -> Reverse[#2] &, ResourceFunction["VertexStratify"][g0], {2}]]]]
Out[5]=

Arrange vertices of a RandomGraph along a horizontal time axis:

In[6]:=
With[{g0 = (SeedRandom["GraphTest"]; DirectedGraph[RandomGraph[{10, 15}], "Acyclic"])}, Graph[EdgeList@g0, VertexCoordinates -> Flatten[ MapIndexed[#1 -> (#2 + {0, RandomReal[.75]}) &, ResourceFunction["VertexStratify"][g0], {2}]]]]
Out[6]=

Color nodes of a grid graph according to their distance from a corner:

In[7]:=
With[{strat = ResourceFunction["VertexStratify"][ GridGraph[{10, 10}, DirectedEdges -> True]]}, GridGraph[{10, 10}, DirectedEdges -> True, VertexSize -> 1/3, EdgeStyle -> Directive[Gray, Arrowheads[0.03]], VertexStyle -> (Flatten[MapIndexed[Function[{verts, ind}, # -> Hue[ind[[1]]/20] & /@ verts], strat]])]]
Out[7]=

Plot a tree graph according to different vertex stratifications:

In[8]:=
With[{strat = ResourceFunction["VertexStratify"][ KaryTree[20, 2, DirectedEdges -> True], 0]}, Row[Function[{graphs}, Join[ graphs[[1 ;; 2]], {Style[ "... " <> ToString[Length[strat] - 3] <> " ... ", Gray], graphs[[3]]}] ][Graph[EdgeList@KaryTree[20, 2, DirectedEdges -> True], VertexCoordinates -> Flatten[ MapIndexed[#1 -> Plus[Reverse[#2], {RandomReal[0.5], 0}] &, #, {2}]], ImageSize -> {Automatic, 100} ] & /@ RandomSample[strat, 3]], ", "] ]
Out[8]=

The output of GridGraph is rigid in the sense of having only one stratification of minimal length:

In[9]:=
Length@ResourceFunction["VertexStratify"][ GridGraph[{2, 2}, DirectedEdges -> True], 0]
Out[9]=

If the time axis is extended, more foliations can be obtained (cf. oeis.org/A002415):

In[10]:=
Length@ResourceFunction["VertexStratify"][ GridGraph[{2, 2}, DirectedEdges -> True], #] & /@ Range[0, 8]
Out[10]=

If a graph is extremely non-rigid, a cutoff can be given to limit the number of results returned:

In[11]:=
With[{g0 = (SeedRandom["GraphTest"]; DirectedGraph[RandomGraph[{1000, 1000}], "Acyclic"])}, Length@ResourceFunction["VertexStratify"][g0, 0, 2]]
Out[11]=

Possible Issues (1) 

VertexStratify does not accept undirected graphs as inputs:

In[12]:=
ResourceFunction["VertexStratify"][GridGraph[{3, 3}]]
Out[12]=

Neat Examples (1) 

Highlight the stratification-rigid subgraph of a random graph:

In[13]:=
With[{g0 = (SeedRandom["RigidTest"]; DirectedGraph[RandomGraph[{15, 30}], "Acyclic"])}, HighlightGraph[g0, Subgraph[g0, Flatten[Intersection @@@ Transpose[ ResourceFunction["VertexStratify"][g0, 0]]]]]]
Out[13]=

Publisher

Brad Klee

Version History

  • 1.1.0 – 07 November 2022
  • 1.0.0 – 17 June 2022

Related Resources

License Information