Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VertexSizeScaledGraph

Source Notebook

Visualize a graph with scaled vertex size based on custom graph related measures

Contributed by: Soutick Saha

ResourceFunction["VertexSizeScaledGraph"][graph]

visualize a graph with scaled VertexSize based on on custom graph related measures.

Details and Options

GraphPlot is used by default when total EdgeCount is more than 10000.
By default the size of the vertices is scaled based on its VertexDegree.
"MaxVertexSize" in Options is the maximum possible size of a vertex.
"VertexSizeScalingFunction" is a pure function that can act on reals and integers.
VertexSizeScaledGraph can take all options of Graph and GraphPlot and the following Options:
"MaxVertexSize"1maximum size of a vertex
"VertexSizeScalingFunction"Automatichow VertexSize is scaled
"VertexSizeFunction"(VertexDegree[#] &)function to scale the VertexSize
"VertexColoringFunction"Automaticfunction to color the vertices
ColorFunction"Rainbow"ways to color vertices
"VertexSizeFunction" accepts a function whose input is a graph and the output is a list of desired scaled values, such as: VertexDegree, BetweennessCentrality or LocalClusteringCoefficient.
The Option ColorFunction can be used when "VertexColoringFunction" is a pure function that can act on a Graph and return numerical values corresponding to each Vertex.

Examples

Basic Examples (4) 

Visualize the VertexSizeScaledGraph of the Golomb graph:

In[1]:=
ResourceFunction["VertexSizeScaledGraph"][GraphData["GolombGraph"]]
Out[1]=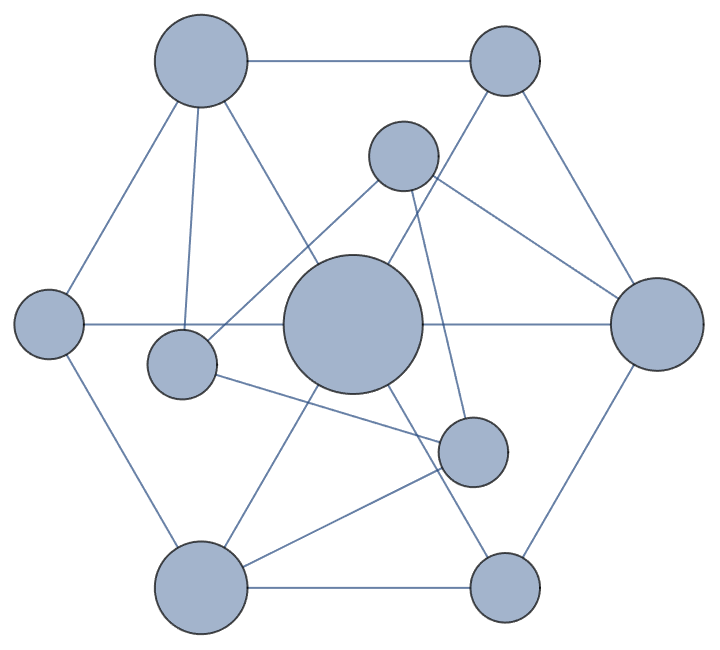

Limit the maximum vertex size with various graphs:

In[2]:=
ResourceFunction["VertexSizeScaledGraph"][GraphData[#], "MaxVertexSize" -> 0.4] & /@ {"BislitCube", "PetersenGraph", "SoiferGraph", "TilleyGraph", "FritschGraph", "HerschelGraph"}
Out[2]=

Visualize VertexSizeScaledGraph of a RandomGraph:

In[3]:=
n = 50; m = 6*n; ResourceFunction["VertexSizeScaledGraph"][RandomGraph[{n, m}]]
Out[5]=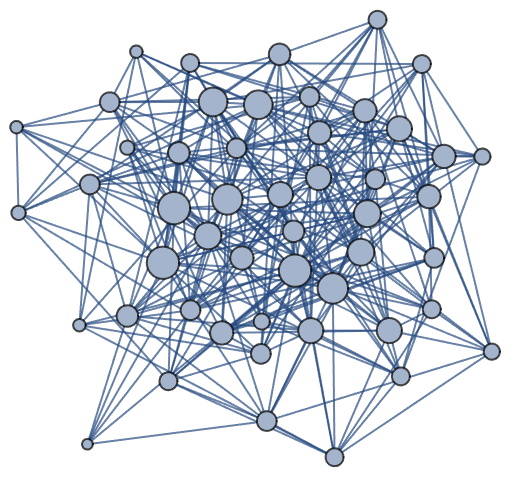

Also works on directed graphs:

In[6]:=
ResourceFunction["VertexSizeScaledGraph"][ Graph[DirectedEdge @@@ RandomSample[Subsets[Range[8], {2}], 20]], "MaxVertexSize" -> 0.3]
Out[6]=

Options (7) 

MaxVertexSize (1) 

Set the maximum VertexSize of a Graph:

In[7]:=
ResourceFunction["VertexSizeScaledGraph"][ ResourceData["Bipartite Diseasome Network"], "MaxVertexSize" -> 50, VertexStyle -> RGBColor[0.68, 0.68, 0], EdgeStyle -> RGBColor[0., 0.061999999999999944`, 0.06799999999999995] ]
Out[7]=

VertexSizeFunction (1) 

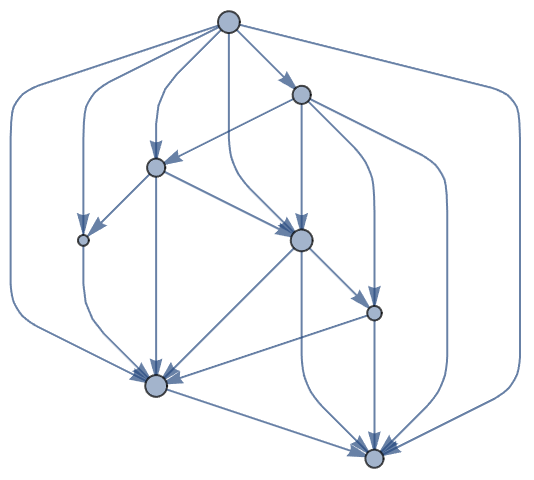VertexSizeScaledGraph of SoiferGraph where the VertexSize is scaled by different measures:

In[8]:=
Map[ResourceFunction["VertexSizeScaledGraph"][ GraphData["SoiferGraph"], "VertexSizeFunction" -> #] &, {(VertexDegree[#] &), (BetweennessCentrality[#] &), (LocalClusteringCoefficient[#] &), (EigenvectorCentrality[#] &)}]
Out[8]=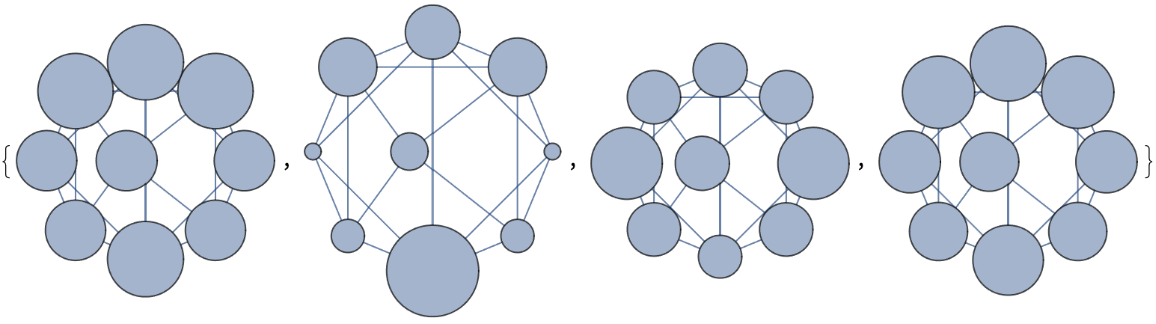

VertexSizeScalingFunction (2) 

VertexSizeScaledGraph of the Actinobacillus Actinomycetemcomitans Metabolic Network scaled in two different ways:

In[9]:=
ResourceFunction["VertexSizeScaledGraph"][ ResourceData[ "Actinobacillus Actinomycetemcomitans Metabolic Network"], "VertexSizeScalingFunction" -> (Log2[#] &), "MaxVertexSize" -> 30, VertexStyle -> RGBColor[0.91, 0.68, 0], EdgeStyle -> RGBColor[0, 0.58, 0.61]]
Out[9]=
In[10]:=
ResourceFunction["VertexSizeScaledGraph"][ ResourceData[ "Actinobacillus Actinomycetemcomitans Metabolic Network"], "VertexSizeScalingFunction" -> (#^0.5 &), "MaxVertexSize" -> 40, VertexStyle -> RGBColor[0.91, 0.68, 0], EdgeStyle -> RGBColor[0, 0.58, 0.61]]
Out[10]=

VertexColoringFunction (1) 

VertexSizeScaledGraph of the GolombGraph with vertices colored by different measures:

In[11]:=
Map[ResourceFunction["VertexSizeScaledGraph"][ GraphData["GolombGraph"], "VertexColoringFunction" -> #] &, {(VertexDegree[#] &), (BetweennessCentrality[#] &), (LocalClusteringCoefficient[#] &), (ClosenessCentrality[#1] &)}]
Out[11]=

ColorFunction (2) 

VertexSizeScaledGraph of the GolombGraph with vertices colored by different measures and custom ColorFunction:

In[12]:=
Map[ResourceFunction["VertexSizeScaledGraph"][ GraphData["GolombGraph"], "VertexColoringFunction" -> #, ColorFunction -> "DeepSeaColors"] &, {(VertexDegree[#] &), (BetweennessCentrality[#] &), (LocalClusteringCoefficient[#] &), (ClosenessCentrality[#1] &)}]
Out[12]=
In[13]:=
bc = BetweennessCentrality[GraphData["GolombGraph"]]; cF = (Blend[{{Min@bc, RGBColor[0, 0, 1]}, {Mean[{Min@bc, Max@bc}], GrayLevel[1]}, {Max@bc, RGBColor[1, 0, 0]}}, #] &); ResourceFunction["VertexSizeScaledGraph"][GraphData["GolombGraph"], "VertexColoringFunction" -> (BetweennessCentrality[#] &), ColorFunction -> cF]
Out[14]=

Neat Examples (3) 

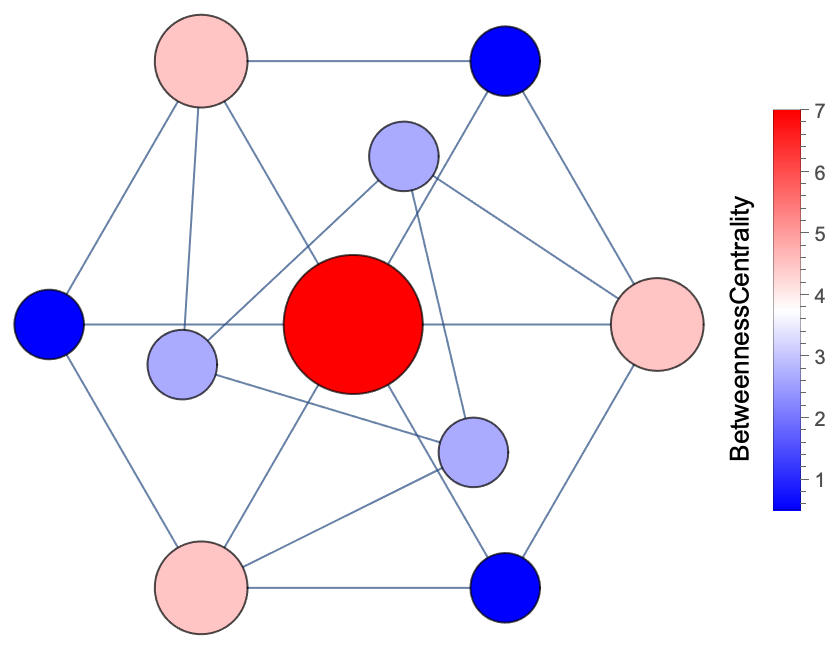VertexSizeScaledGraph of a Disease Gene Network:

In[15]:=
ResourceFunction["VertexSizeScaledGraph"][ ResourceData["Disease Gene Network"], VertexStyle -> RGBColor[0.6, 0.68, 0], EdgeStyle -> RGBColor[0, 0, 0.61], "MaxVertexSize" -> 100]
Out[15]=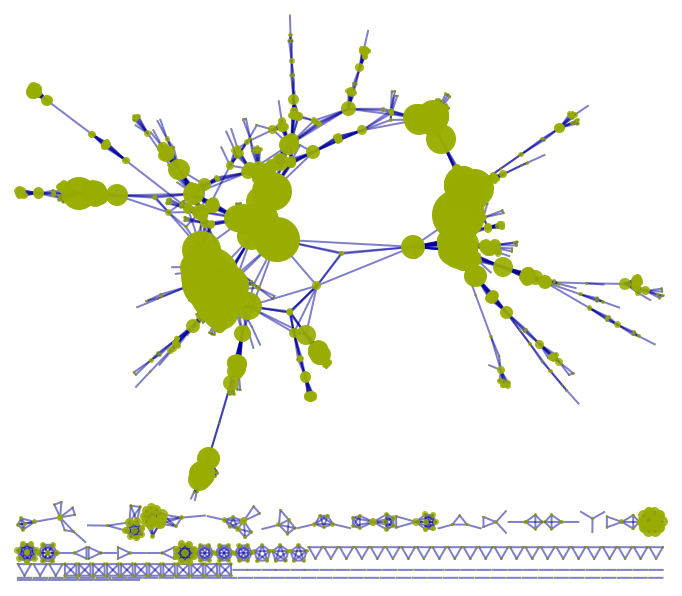

VertexSizeScaledGraph of a Disease Gene Network where the vertices are color-coded by its BetweennessCentrality:

In[16]:=
ResourceFunction["VertexSizeScaledGraph"][ ResourceData["Disease Gene Network"], EdgeStyle -> RGBColor[0, 0, 0.61], "VertexColoringFunction" -> (BetweennessCentrality[#] &), ColorFunction -> "DeepSeaColors", "MaxVertexSize" -> 100]
Out[16]=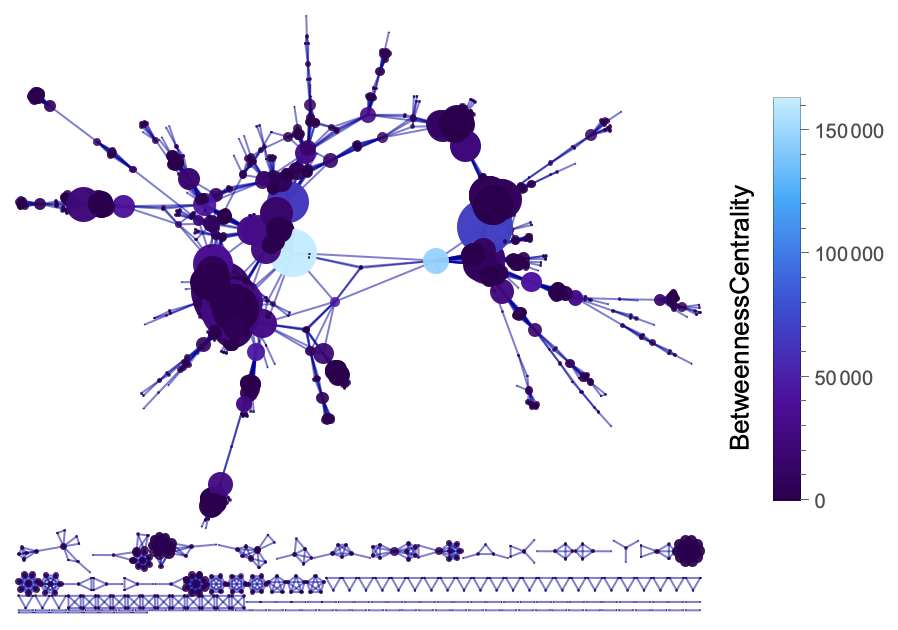

VertexSizeScaledGraph containing randomly chosen genes from the co-expression network in human tissues:

In[17]:=
(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/f0a04af6-5d61-4a45-a535-4eb5b41c8975"]
Out[11]=

Publisher

WolframChemistry

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.1.0 – 01 November 2024
  • 1.0.0 – 25 October 2024

Source Metadata

  • Citation:
    • Barabási, Albert-László, and Réka Albert. "Emergence of scaling in random networks." science 286.5439 (1999): 509-512.

Related Resources

License Information