Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Assign colors to vertices of a graph so that no edge connects vertices of the same color
ResourceFunction["VertexColoring"][g] gives a vertex coloring of graph g. |
| "Brelaz" | Brelaz’s heuristics |
| "Optimum" | exhaustive search for an optimum coloring |
Group vertices of a graph so that no group contains adjacent vertices:
| In[1]:= |
| Out[1]= | 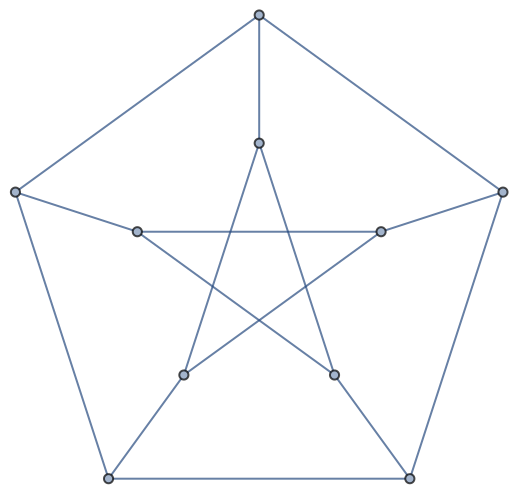 |
| In[2]:= |
| Out[2]= |
Highlight vertices of the same groups:
| In[3]:= |
| Out[3]= | 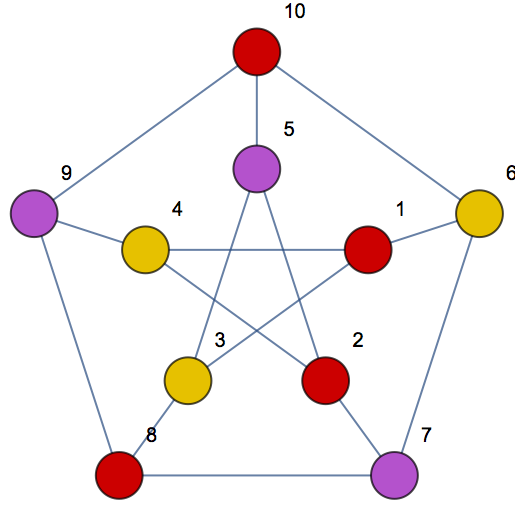 |
Use the specified set of colors:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= | 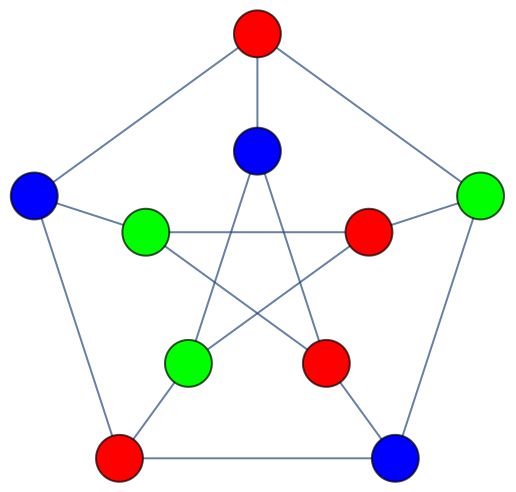 |
VertexColoring works with undirected graphs:
| In[6]:= |
| Out[6]= | 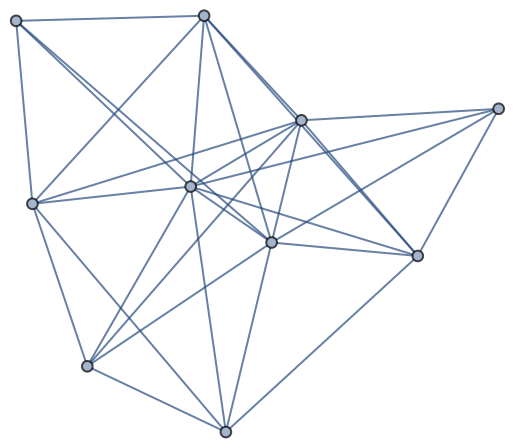 |
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= | 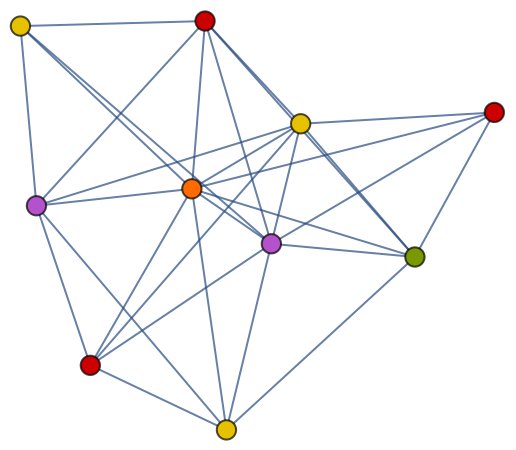 |
Directed graphs:
| In[9]:= |
| Out[9]= | 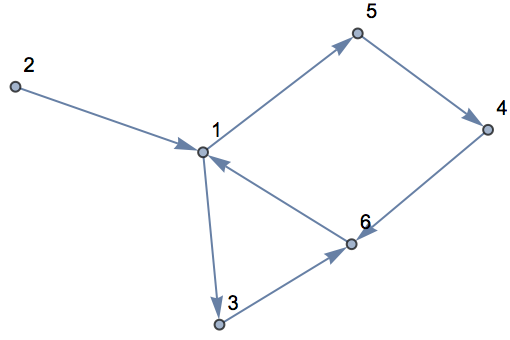 |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= | 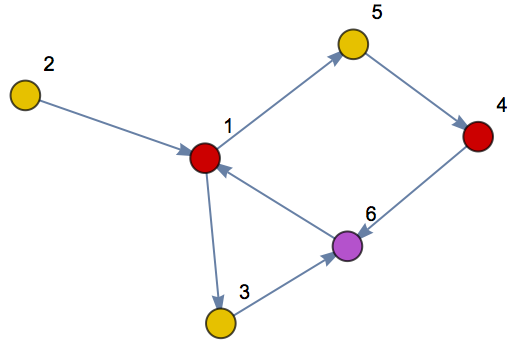 |
Multigraphs:
| In[12]:= | ![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {2, 3}, {3, 1}, {3, 4}, {4, 5}, {5, 3}}, Null}, {EdgeStyle -> {
Arrowheads[Automatic]}, FormatType -> TraditionalForm, GraphLayout -> {"Dimension" -> 2}, GridLinesStyle -> Directive[
GrayLevel[0.5, 0.4]], VertexLabels -> {"Name"}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Automatic], ArrowBox[{{2.017540424146274, 0.00044208442469451104`}, {
2.017313638325164, 0.8021720910704471}}, 0.022753627728707843`], ArrowBox[BezierCurveBox[{{2.017313638325164, 0.8021720910704471}, {1.5786497609293124`, 0.4357165494909167}, {1.008104154360962, 0.40117133112610454`}}], 0.022753627728707843`], ArrowBox[BezierCurveBox[{{2.017313638325164, 0.8021720910704471}, {1.4467680317568175`, 0.7676268727056339}, {1.008104154360962, 0.40117133112610454`}}], 0.022753627728707843`], ArrowBox[{{1.008104154360962, 0.40117133112610454`}, {
2.017540424146274, 0.00044208442469451104`}}, 0.022753627728707843`], ArrowBox[{{1.008104154360962, 0.40117133112610454`}, {0., 0.}}, 0.022753627728707843`], ArrowBox[{{0., 0.}, {0.00022442750785334198`, 0.8026134080747779}}, 0.022753627728707843`], ArrowBox[{{0.00022442750785334198`, 0.8026134080747779}, {
1.008104154360962, 0.40117133112610454`}}, 0.022753627728707843`]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{2.017540424146274, 0.00044208442469451104}, 0.022753627728707843], InsetBox["1", Offset[{2, 2}, {2.040294051874982, 0.023195712153402354}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{2.017313638325164, 0.8021720910704471}, 0.022753627728707843], InsetBox["2", Offset[{2, 2}, {2.040067266053872, 0.8249257187991549}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{1.008104154360962, 0.40117133112610454}, 0.022753627728707843], InsetBox["3", Offset[{2, 2}, {1.0308577820896698, 0.4239249588548124}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.022753627728707843], InsetBox["4", Offset[{2, 2}, {0.022753627728707843, 0.022753627728707843}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {
DiskBox[{0.00022442750785334198, 0.8026134080747779}, 0.022753627728707843], InsetBox["5", Offset[{2, 2}, {0.022978055236561185, 0.8253670358034857}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]]]\);](https://www.wolframcloud.com/obj/resourcesystem/images/999/99917a65-d19a-4547-8c1c-f64279a7ee49/139636da128a61b8.png) |
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= | 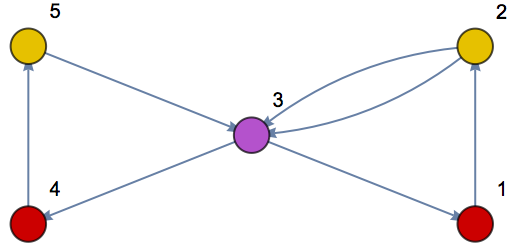 |
Mixed graphs:
| In[15]:= |
| Out[15]= |  |
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= |  |
Graphs with symbolically defined vertices:
| In[18]:= |
| Out[18]= | 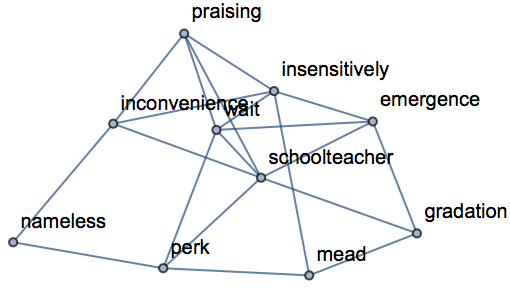 |
| In[19]:= |
| Out[19]= |
| In[20]:= |
| Out[20]= | 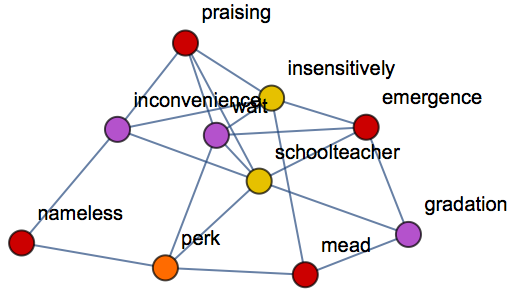 |
By default, VertexColoring uses Brelaz’s heuristics, which does not necessarily give minimum coloring:
| In[21]:= |
| Out[21]= | 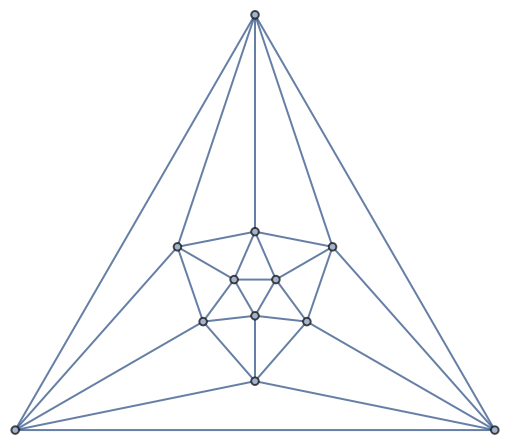 |
| In[22]:= |
| Out[22]= |
In this case, a 5-coloring is produced:
| In[23]:= |
| Out[23]= |
| In[24]:= |
| Out[24]= | 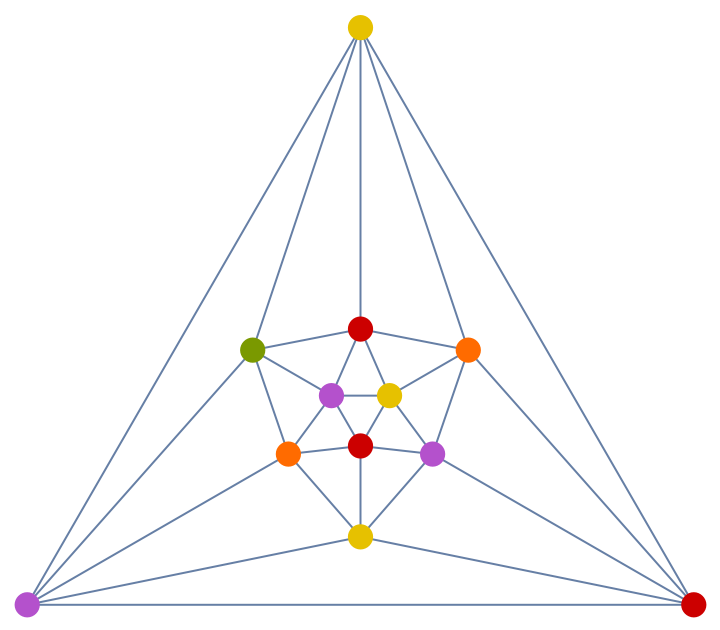 |
However, the minimum coloring should use only four colors, as given by the chromatic number of the graph:
| In[25]:= |
| Out[25]= |
Obtain minimum coloring using Method→"Optimum":
| In[26]:= |
| Out[26]= |
| In[27]:= |
| Out[27]= |
| In[28]:= |
| Out[28]= | 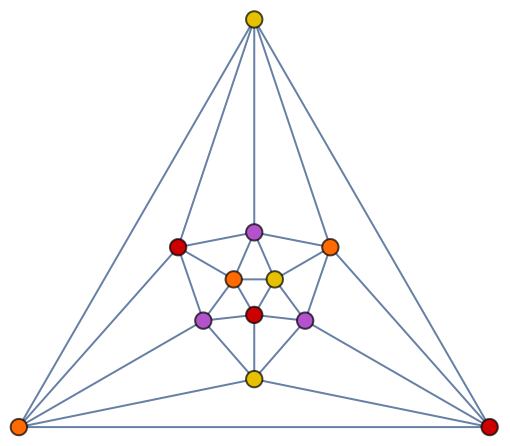 |
The default Brelaz’s heuristic can produce minimum coloring for some graphs:
| In[29]:= |
| Out[29]= | 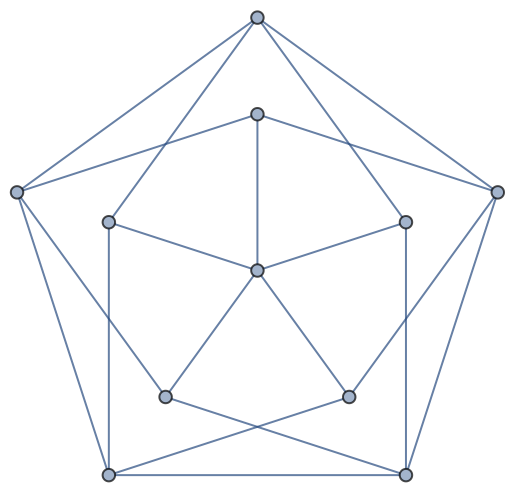 |
| In[30]:= |
| Out[30]= |
| In[31]:= |
| Out[31]= |
| In[32]:= |
| Out[32]= | 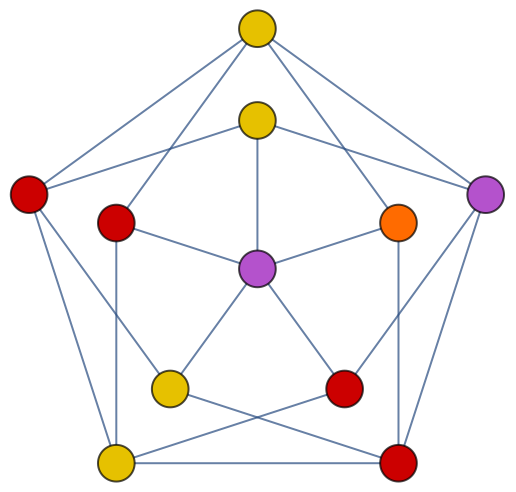 |
The Brelaz heuristic is optimal for trees:
| In[33]:= |
| Out[33]= | 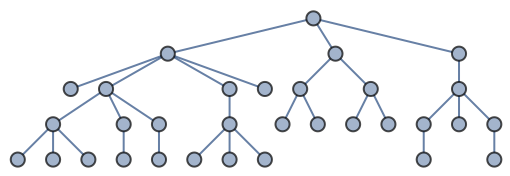 |
| In[34]:= |
| Out[34]= |
| In[35]:= |
| Out[35]= | 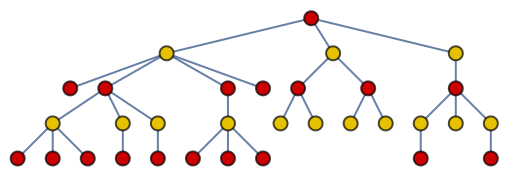 |
The Brelaz heuristic is also optimal for complete graphs, which, by definition, are n-colorable:
| In[36]:= |
| Out[36]= | 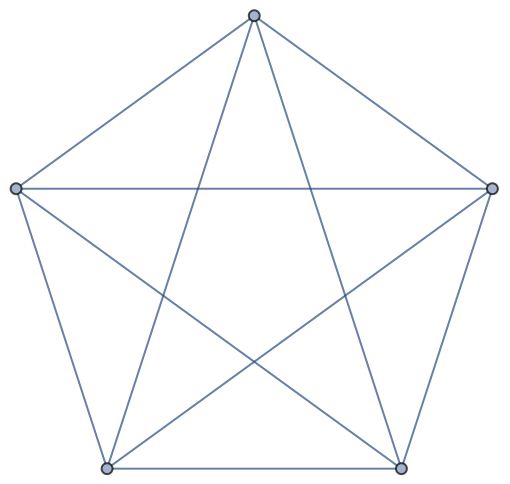 |
| In[37]:= |
| Out[37]= |
Likewise, the Brelaz heuristic is optimal for complete k-partite graphs that are k-colorable:
| In[38]:= |
| Out[38]= |  |
| In[39]:= |
| Out[39]= |
| In[40]:= |
| Out[40]= | 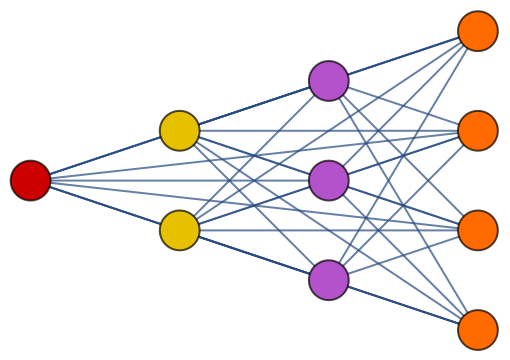 |
Grid graphs are bipartite, for the vertices can be partitioned like the squares on a chessboard:
| In[41]:= |
| Out[41]= | 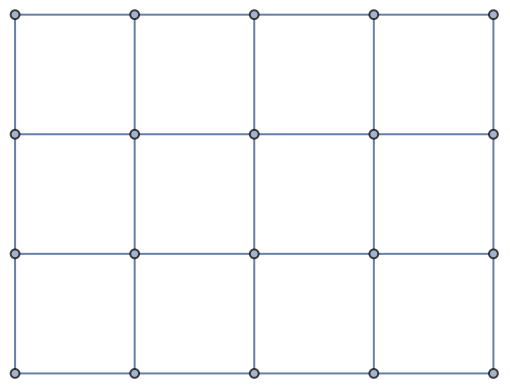 |
| In[42]:= |
| Out[42]= |
| In[43]:= |
| Out[43]= | 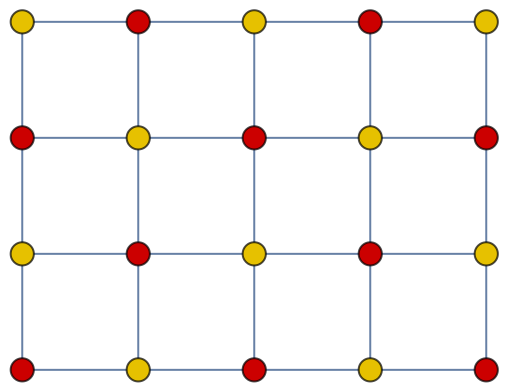 |
ChromaticPolynomial can be used to find the chromatic number of a graph:
| In[44]:= |
| Out[44]= | 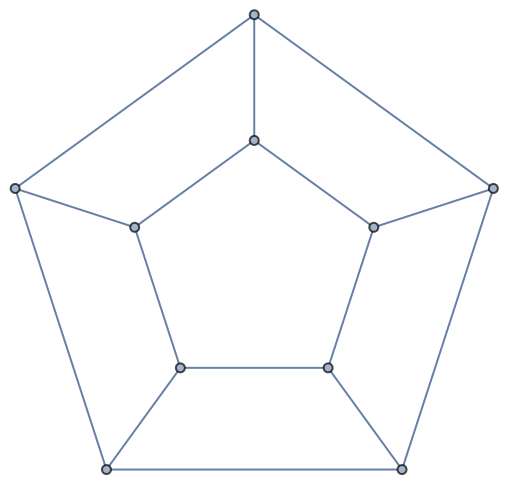 |
| In[45]:= |
| Out[45]= |
| In[46]:= |
| Out[46]= |
The coloring corresponding the this chromatic number:
| In[47]:= |
| Out[47]= |
| In[48]:= |
| Out[48]= | 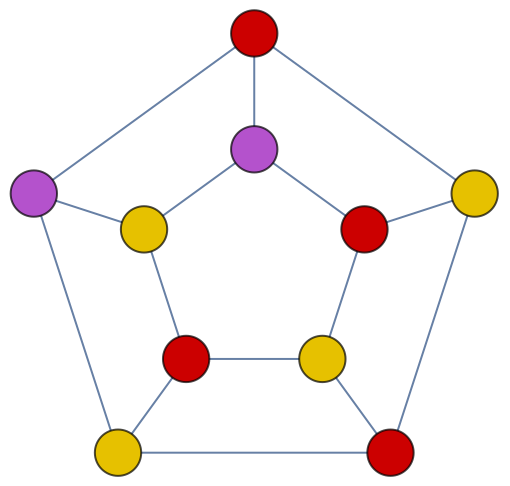 |
This work is licensed under a Creative Commons Attribution 4.0 International License