Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 VertexArc

Source Notebook

Graphics primitive for the arc of a polygon vertex

Contributed by: Ed Pegg Jr and Eric Weisstein

ResourceFunction["VertexArc"][{q1,p,q2},rad]

constructs a circular arc centered at p with radius rad from vertex points p,q1 and q2.

Examples

Basic Examples (2) 

Form a vertex arc:

In[1]:=
pythag = {{5, 0}, {0, 0}, {3, 4}}; ResourceFunction["VertexArc"][pythag, 1]
Out[2]=

Show the arc and vertex:

In[3]:=
Graphics[{Line[pythag], Blue, ResourceFunction["VertexArc"][pythag, 1]}, ImageSize -> Small]
Out[3]=

Scope (3) 

Four non-congruent triangles with three shared angles and various shared sides:

In[4]:=
pts = {{0, Root[-1 - #^2 + #^4& , 2, 0]}, {0, 0}, {1, 0}, {(1/2) (1 + Sqrt[5]), Root[-1 - #^2 + #^4& , 2, 0]}, {(1/2) (1 + Sqrt[5]), Root[-1 + #^2 + #^4& , 2, 0]}, {1, Root[-1 + #^2 + #^4& , 2, 0]}, {(1/2) (1 + Sqrt[5]), 0}}; Graphics[{Thick, Line[pts[[{5, 6}]]], Red, Line[pts[[{4, 1, 3}]]], Magenta, Line[pts[[{2, 3, 5}]]], Darker[Yellow], Line[pts[[{1, 2, 6}]]], Brown, Line[pts[[{4, 6, 3}]]], Blue, ResourceFunction["VertexArc"][pts[[#]], 0.15] & /@ {{1, 2, 3}, {4, 1, 2}, {3, 6, 5}, {2, 3, 6}}, Green, ResourceFunction["VertexArc"][pts[[#]], 0.22] & /@ {{2, 3, 1}, {1, 2, 4}, {6, 5, 3}, {3, 6, 2}}, Cyan, ResourceFunction["VertexArc"][pts[[#]], 0.2] & /@ {{3, 1, 2}, {2, 4, 1}, {5, 3, 6}, {6, 2, 3}}}]
Out[5]=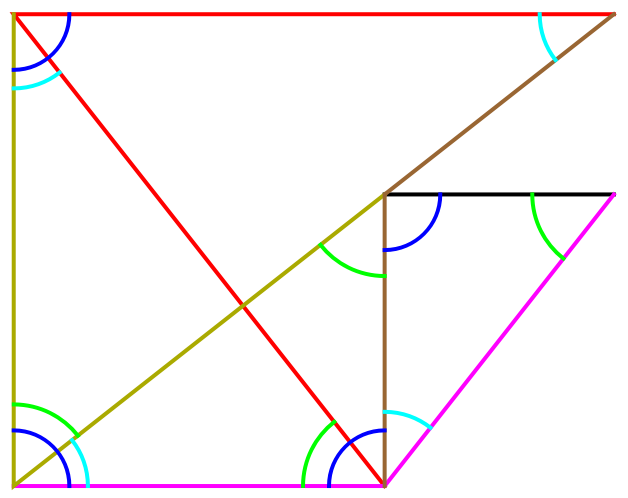

A rectangle dissected into seven similar triangles:

In[6]:=
psi = RootReduce[Sqrt[ Root[-1 - #^2 + #^3& , 1, 0]]]; p5 = {{0, 0}, {psi^3, 0}, {0, psi^5}, {psi^3, psi^5}, { Root[-1 + 4 #^2 - 3 #^4 + #^6& , 2, 0], Root[-1 + 3 #^2 - 4 #^4 + #^6& , 2, 0]}, {0, psi^7}, {psi^9, 0}, {psi^9, psi^7}, { Root[-1 + 7 #^2 - 15 #^4 + #^6& , 2, 0], Root[-1 - #^4 + #^6& , 2, 0]}}; tri = {{3, 5, 4}, {6, 3, 4}, {4, 5, 2}, {2, 1, 3}, {7, 9, 8}, {4, 2, 7}, {8, 9, 6}}; Graphics[{EdgeForm[{Black}], White, Polygon[p5[[#]]] & /@ tri, Red, ResourceFunction["VertexArc"][p5[[#]], 0.5] & /@ tri, Blue, ResourceFunction["VertexArc"][RotateRight[p5[[#]]], 0.5] & /@ tri, Green, ResourceFunction["VertexArc"][RotateLeft[p5[[#]]], 0.5] & /@ tri}]
Out[8]=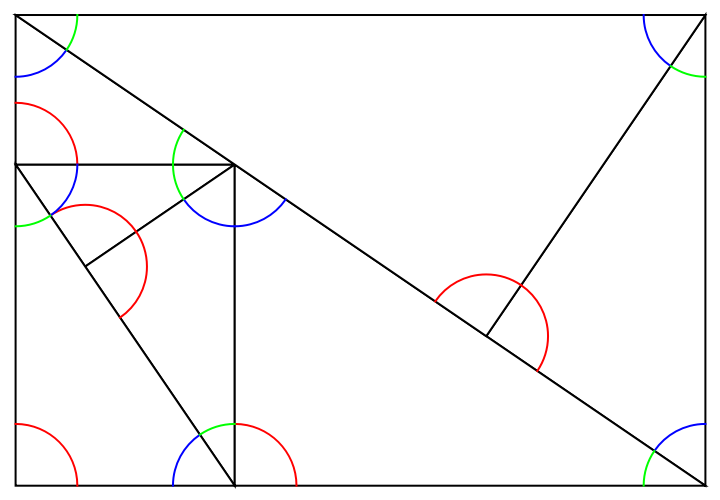

Depict the angles of an arrowhead quadrilateral:

In[9]:=
pts = {{1, 1}, {0, 0}, {-1, 1}, {0, -2}}; Graphics[{{FaceForm[White], EdgeForm[Black], Polygon[pts]}, MapIndexed[{ColorData[41] @@ #2, ResourceFunction["VertexArc"][#, 0.5]} &, Partition[pts, 3, 1, 1]]}]
Out[10]=

Possible Issues (1) 

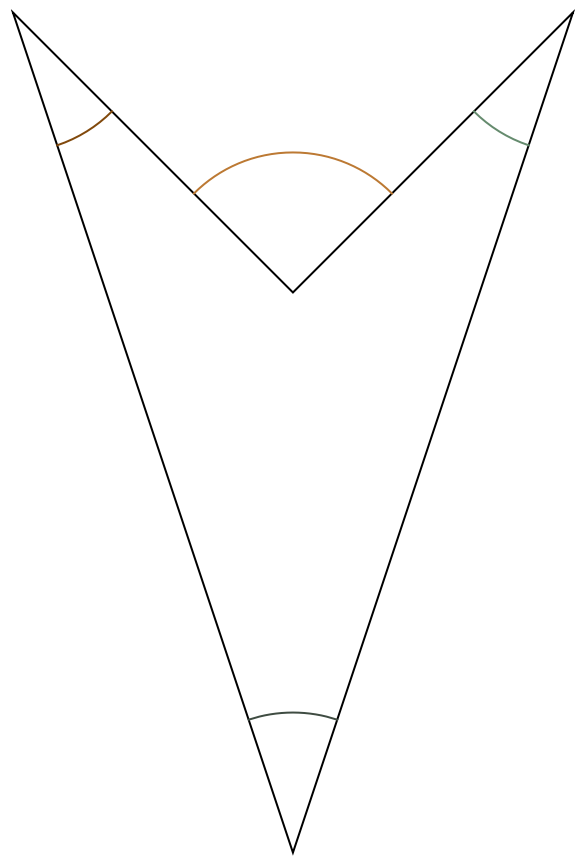For a 180°, the resulting arc is arbitrarily oriented:

In[11]:=
{Graphics[ResourceFunction["VertexArc"][{{1, 0}, {0, 0}, {-1, 0}}]], Graphics[ResourceFunction["VertexArc"][{{-1, 0}, {0, 0}, {1, 0}}]]}
Out[11]=

Neat Examples (1) 

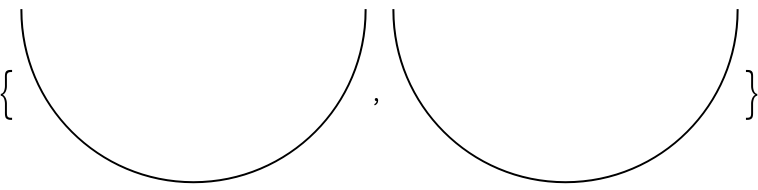In the psi-quad substitution tiling, :

In[12]:=
psI = \[Psi] /. Solve[\[Psi]^3 == \[Psi]^2 + 1][[3]]; pts = RootReduce[ReIm[Join[ \!\(\*SuperscriptBox[\(psI\), \({0, 1, 2, 3, 4}\)]\), {-psI^2}]]]; polys = {{1, 2, 3, 4}, {2, 3, 4, 5}, {5, 4, 1, 6}}; Graphics[{EdgeForm[Black], White, Opacity[.5], Polygon[pts[[#]]] & /@ polys, Opacity[1], Red, ResourceFunction["VertexArc"][pts[[#[[{2, 3, 4}]]]], 0.21] & /@ polys, Blue, ResourceFunction["VertexArc"][pts[[#[[{1, 2, 3}]]]], 0.19] & /@ polys, Green, ResourceFunction["VertexArc"][pts[[#[[{3, 4, 1}]]]], 0.15] & /@ polys }]
Out[13]=

Version History

  • 1.0.0 – 03 May 2022

Related Resources

License Information