Function Repository Resource:

VerifyMTP

Prove or disprove a closed first-order formula in the theory of univariate mixed trigonometric polynomials

Contributed by: Rizeng Chen (xiaxueqaq)

ResourceFunction["VerifyMTP"][formula]

returns the truth value of a mixed trigonometric polynomial represented by formula.

Details

A mixed trigonometric polynomial expression is often referred to as an MTP.

The input formula must be a closed (i.e. fully quantified) formula in the first order theory of univariate mixed trigonometric polynomials. Since there is only one variable in this theory, a legal input should be a ForAll or Exists quantified expression.

Only univariate mixed trigonometric polynomials with rational and/or integer coefficients are allowed in formula, and all denominators should be cleared. That is to say, the input should a polynomial in the variable itself or sines and/or cosines of the variable.

When the input is a ForAll expression, the result can be True or {False,point}. In the latter case, point comprises a counterexample.

Similarly, when the input is an Exists expression, the result can be {True,point} or False. The former case gives an instance.

Examples

Basic Examples (1)

Prove that if x is a positive solution to x²=tanx, then x>1:

In[1]:=

$ResourceFunction["VerifyMTP"][ ForAll[x, x^2 Cos[x] - Sin[x] == 0 && x > 0 \[Implies] -1 + x > 0]]$

Out[1]=

Scope (2)

Verify a formula in the first order theory of MTPs:

In[2]:=

$ResourceFunction["VerifyMTP"][ ForAll[x, -2 + x > 0 && -16 - x^4 + (-16 + x^4) Cos[x] + 2 x (4 + x^2) Sin[x] > 0 \[Implies] 2 - x + (2 + x) Cos[x] > 0]]$

Out[2]=

Verify a complicated example:

In[3]:=

$ResourceFunction["VerifyMTP"][ ForAll[x, Sin[x] != 0 \[Implies] -x^4 (25 + x^2)^2 Sin[x]^2 + x^4 (25 + x^2)^2 Cos[x]^2 Sin[x]^2 + x^8 Sin[x]^4 != 0]]$

Out[3]=

Applications (2)

Prove MTP inequalities:

In[4]:=

Out[4]=

Show that is a point on the curve given by x=sin t, y=sin 2t by finding an explicit value for t:

In[5]:=

ResourceFunction["VerifyMTP"][
Exists[t, -(15/16) + Sin[t]^2 == 0 && -(15/64) + TrigExpand[Sin[2 t]^2] == 0 && Sin[t] > 0 && TrigExpand[Sin[2 t]] > 0]]

Out[5]=

Properties and Relations (3)

When x is bounded, Reduce can be used:

In[6]:=

$Reduce[ForAll[x, 0 < x < 1, ((Sin[x] - x + x^2 > 0) \[And] (Sin[x] - x < 0))], x]$

Out[6]=

In[7]:=

$ResourceFunction["VerifyMTP"][ ForAll[x, ((x > 0) \[And] (x - 1 < 0)) \[Implies] ((Sin[x] - x + x^2 > 0) \[And] (Sin[x] - x < 0))]]$

Out[7]=

When x is unbounded, Reduce is not able to give a result:

In[8]:=

Out[8]=

VerifyMTP handles this input however:

In[9]:=

Out[9]=

Neat Examples (2)

Show that the circle 25x²+25(y-3)²=36 is disjoint from the parametric curve x=tcos²t, y=t sin t:

In[10]:=

Out[10]=

Note that it is very hard to tell from a plot if the two curves are disjoint:

In[11]:=

$Show[ParametricPlot[{t Cos[t]^2, t Sin[t]}, {t, -4 Pi, 4 Pi}, Frame -> True, Axes -> False, PlotTheme -> "Web"], ContourPlot[25 x^2 + 25 (y - 3)^2 == 36, {x, -2, 2}, {y, 1, 5}]]$

Out[11]=

Publisher

Rizeng Chen

Requirements

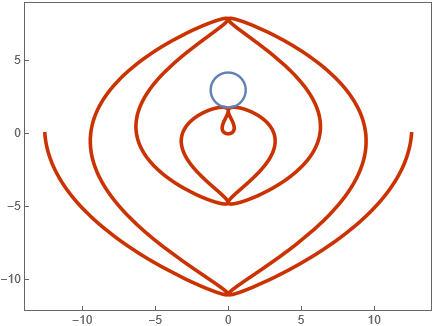Wolfram Language 13.0 (December 2021) or above

Version History

1.0.0 – 15 December 2023

Source Metadata

Citation:
- Chen, Rizeng, and Bican Xia. "Deciding first-order formulas involving univariate mixed trigonometric-polynomials." Proceedings of the 2023 International Symposium on Symbolic and Algebraic Computation. 2023.
- Rizeng Chen, Haokun Li, Bican Xia, Tianqi Zhao, Tao Zheng. Isolating all the real roots of a mixed trigonometric-polynomial. Journal of Symbolic Computation, Volume 121, 2024. DOI: 10.1016/j.jsc.2023.102250.

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

VerifyMTP

Details