Function Repository Resource:

UpToBinaryCompositions

List all possible unary and binary combinations for a chosen set of functions and symbols

Contributed by: Bradley Klee

ResourceFunction["UpToBinaryCompositions"][leafn,sym,unaries,binaries]

returns all possible compositions of symbols listed in sym by unary and binary functions listed in unaries and binaries, whose proper leaf count (terminal nodes only) equals leafn.

Details

Arguments unaries and binaries are lists, which should contain unary and binary functions, respectively.

Exactly one unary function from unaries is applied around each leaf and around each branch point, including the root, so unaries must usually contain Identity.

Binary functions are applied similarly to Groupings, but to all possible orderings of atomistic symbols listed in sym.

Examples

Basic Examples (1)

Mimic the functionality of the resource function BinaryCompositions:

In[1]:=

$TableForm[ ResourceFunction[ "UpToBinaryCompositions"][#, {\[FormalA], \[FormalB]}, {Identity}, {SmallCircle}] & /@ {1, 2, 3}]$

Out[1]=

Properties and Relations (2)

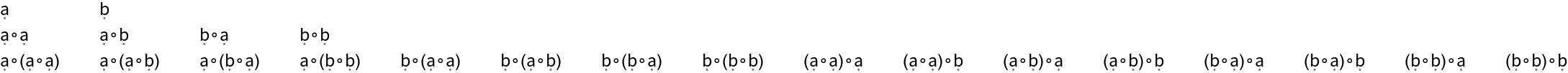Compare UpToBinaryCompositions with Groupings by treating outputs as sets (A and B respectively):

In[2]:=

$With[{setsData = { ResourceFunction["UpToBinaryCompositions"][ 2, {\[FormalA]}, {Identity, Square}, {Wedge, Vee}], Groupings[{\[FormalA], \[FormalA]}, {Identity -> 1, Square -> 1, Wedge -> 2, Vee -> 2}]}}, Grid[MapThread[{#1, Row[#2, ", "]} &, { {"A∩B", "A\[Backslash]B", "B\[Backslash]A"}, {Intersection @@ #, Complement @@ #, Complement @@ Reverse[#]} &@ setsData}], Frame -> All, FrameStyle -> LightGray, Spacings -> {1, 1}] ]$

Out[2]=

Test the Catalan counting property:

In[3]:=

$Table[Length[ ResourceFunction["UpToBinaryCompositions"][ k, {\[FormalA], \[FormalB]}, {Identity, Square}, {Wedge, Vee, SmallCircle}]]/(2 2)^k/(2 3)^(k - 1), {k, 5}]$

Out[3]=

In[4]:=

Out[4]=

Possible Issues (1)

Without specifying at least one unary operator, no combinations are possible:

In[5]:=

$ResourceFunction[ "UpToBinaryCompositions"][#, {\[FormalA], \[FormalB]}, {}, {SmallCircle}] & /@ {1, 2, 3}$

Out[5]=

Neat Examples (2)

Count Boolean tautologies out of a finite set of compositions:

In[6]:=

$Count[TautologyQ /@ ResourceFunction["UpToBinaryCompositions"][ 2, {\[FormalA], \[FormalB]}, {Identity, Not}, {And, Or, Equivalent}], True]$

Out[6]=

Generate a complicated polynomial data structure:

In[7]:=

$SortedPolynomialData = Map[Function[{row}, SortBy[Tally[row], -#[[1]] &]], MapIndexed[CoefficientList[#, \[FormalA], #2[[1]]] &, ResourceFunction["UpToBinaryCompositions"][#, {1}, {# &}, {(#1 + #2) \[FormalA] &}] & /@ Range[1, 12], {2}]];$

Count degeneracies and put them in a table:

In[8]:=

$TableForm[ SortedPolynomialData[[1 ;; 8]] /. {{x_List, y_Integer} :> y}]$

Out[8]=

Compare row lengths with OEIS core sequence A002572:

In[9]:=

Out[9]=

Compare last term of each row with relatively new OEIS sequence A345135:

In[10]:=

$Part[SortedPolynomialData /. {{x_List, y_Integer} :> y}, All, -1]$

Out[10]=

Compare row weights with OEIS core sequence A000984:

In[11]:=

$Total /@ (SortedPolynomialData /. {{x_List, y_Integer} :> Total[x]*y})$

Out[11]=

Explore the effects of perturbing the unary function away from identity:

In[12]:=

$With[{SortedPolynomialData = Map[Function[{row}, SortBy[Tally[row], -#[[1]] &]], MapIndexed[CoefficientList[#, \[FormalA], #2[[1]]] &, ResourceFunction["UpToBinaryCompositions"][#, {1}, {# + \[FormalA] &}, {(#1 + #2) \[FormalA] &}] & /@ Range[1, 12], {2}]]}, Column[{Length /@ #, Part[# /. {{x_List, y_Integer} :> y}, All, -1], Total /@ (# /. {{x_List, y_Integer} :> Total[x]*y}) } &[SortedPolynomialData]]]$