Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the unwinding number
ResourceFunction["UnwindingNumber"][z] gives the unwinding number 𝒰(z). |
Evaluate numerically:
| In[1]:= |
| Out[1]= |
Plot of the unwinding number in the complex plane:
| In[2]:= | ![ComplexPlot3D[ResourceFunction["UnwindingNumber"][z], {z, 4 \[Pi]}, ColorFunction -> {ColorData[97, 2] &, None}, Mesh -> True, MeshFunctions -> {Re[#1] &, Im[#1] &}]](https://www.wolframcloud.com/obj/resourcesystem/images/15c/15c2cef8-906f-4434-961c-ee4283f69515/678ab1e35925abd3.png) |
| Out[2]= | 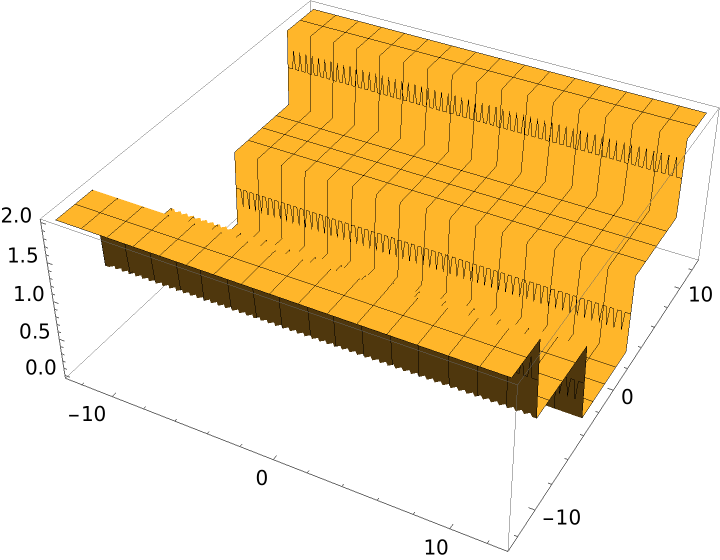 |
Evaluate the unwinding number of a Root object:
| In[3]:= |
| Out[3]= |
Evaluate the unwinding number of a machine precision number:
| In[4]:= |
| Out[4]= |
Evaluate the unwinding number of an arbitrary precision number:
| In[5]:= |
| Out[5]= |
UnwindingNumber threads elementwise over lists:
| In[6]:= |
| Out[6]= |
The identity ![]() does not generally hold for complex z and w:
does not generally hold for complex z and w:
| In[7]:= |
| Out[7]= |
Use the unwinding number to construct a formula that is valid in the entire complex plane:
| In[8]:= |
| Out[8]= |
The identity ![]() does not generally hold for complex z and w:
does not generally hold for complex z and w:
| In[9]:= |
| Out[9]= |
Use the unwinding number to construct a formula that is valid in the entire complex plane:
| In[10]:= |
| Out[10]= |
A relationship between the inverse sine and the inverse tangent:
| In[11]:= | ![ArcSin[z] == ArcTan[z/Sqrt[
1 - z^2]] + \[Pi] (ResourceFunction[
"UnwindingNumber"][-Log[1 + z]] - ResourceFunction["UnwindingNumber"][-Log[1 - z]]) /. z -> -5.1](https://www.wolframcloud.com/obj/resourcesystem/images/15c/15c2cef8-906f-4434-961c-ee4283f69515/1f60813d694fb115.png) |
| Out[11]= |
The unwinding number is an integer:
| In[12]:= |
| Out[12]= |
Compare UnwindingNumber with one of its definitions:
| In[13]:= | ![ResourceFunction["UnwindingNumber"][z] == (z - Log[E^z])/(
2 \[Pi] I) /. z -> RandomComplex[5 \[Pi] (1 + I) {-1, 1}, WorkingPrecision -> $MachinePrecision] // FullSimplify](https://www.wolframcloud.com/obj/resourcesystem/images/15c/15c2cef8-906f-4434-961c-ee4283f69515/744f1d15f8a9489f.png) |
| Out[13]= |
Numerical decision procedures with default settings cannot automatically resolve this value:
| In[14]:= |
| Out[14]= |
Use Simplify to resolve:
| In[15]:= |
| Out[15]= |
Define the Wright omega function:
| In[16]:= |
Visualize the fringing fields of a semi-infinite parallel plate capacitor:
| In[17]:= |
| Out[17]= | 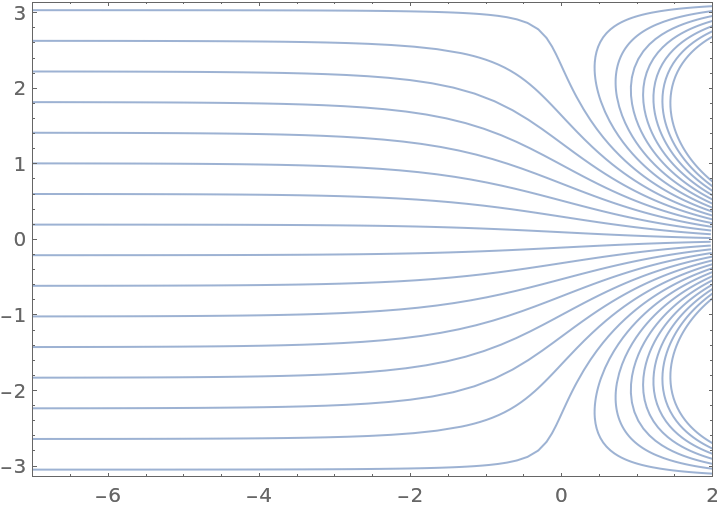 |
This work is licensed under a Creative Commons Attribution 4.0 International License