Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 UnitSystemTransform

Source Notebook

Transform a quantity into a different unit system

Contributed by: Peter Cullen Burbery

ResourceFunction["UnitSystemTransform"][quantity,unitsystem]

transforms quantity into a product of combinations of the basis quantities of unitsystem.

Details

The following unitsystems are currently supported:
"PlanckUnits"the Planck system without electrical units
"NaturalUnits"an extension to the Planck system that spans electrical units with the Von Klitzing constant
"SIDefiningConstants"the seven defining constants of the SI
{q1,q2,…}list of Quantity expressions with appropriate units
"StoneyUnits"the Stoney unit system, similar to the Planck unit system
The output of ResourceFunction["UnitSystemTransform"] is a list, as sometimes the basis will have multiple equivalent dimensional combinations. For example, if the basis quantities span the dimensions but aren’t linearly independent, there will be at least two possible combinations.

Examples

Basic Examples (6) 

Convert to the Planck unit system:

In[1]:=
ResourceFunction["UnitSystemTransform"][ Quantity[1, "Joules"], "PlanckUnits"]
Out[1]=
In[2]:=
ResourceFunction["UnitSystemTransform"][ Quantity[5, "Joules"], "PlanckUnits"]
Out[2]=

Convert to a set of natural units:

In[3]:=
ResourceFunction["UnitSystemTransform"][ Quantity[7, "Webers"], "NaturalUnits"]
Out[3]=

Convert to the SI-defining constants:

In[4]:=
ResourceFunction["UnitSystemTransform"][ Quantity[7, "Webers"], "SIDefiningConstants"]
Out[4]=

Convert to Stoney units:

In[5]:=
ResourceFunction["UnitSystemTransform"][ Quantity[1, "Pascals"] Quantity[1, "Joules"], "StoneyUnits"]
Out[5]=

Convert to a custom combination of quantities:

In[6]:=
ResourceFunction["UnitSystemTransform"][ Quantity[7, "Webers"], {Quantity[1, "GravitationalConstant"], Quantity[1, "ReducedPlanckConstant"], Quantity[1, "VonKlitzingConstant"], Quantity[1, "SpeedOfLight"], Quantity[1, "BoltzmannConstant"]}]
Out[6]=

Find multiple equivalent forms:

In[7]:=
ResourceFunction["UnitSystemTransform"][ Quantity[7, "Webers"], {Quantity[1, "GravitationalConstant"], Quantity[1, "ReducedPlanckConstant"], Quantity[1, "VonKlitzingConstant"], Quantity[1, "SpeedOfLight"], Quantity[1, "BoltzmannConstant"], Quantity[1, "JosephsonConstant"], Quantity[1, "RydbergConstant"]}]
Out[7]=

Possible Issues (1) 

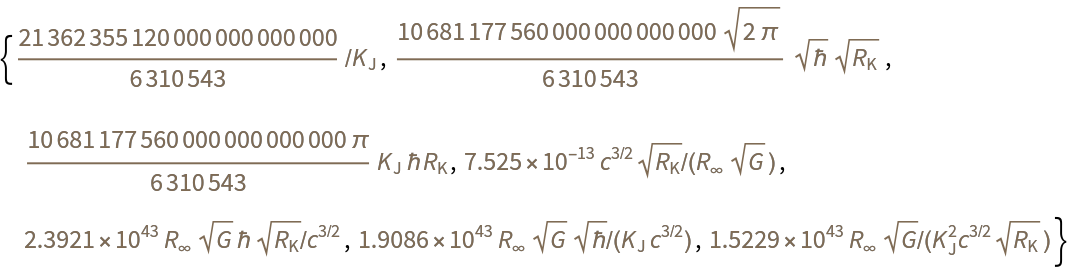If the basis doesn't span the dimensions of the input, the output will be an empty list:

In[8]:=
ResourceFunction["UnitSystemTransform"][ Quantity[1, "Farad"], "PlanckUnits"]
Out[8]=

Publisher

Peter Burbery

Version History

  • 1.0.0 – 07 June 2023

Related Resources

License Information