Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Starting with the third term, give the least integer expressible uniquely as the sum of two distinct earlier terms
ResourceFunction["UlamSequence"][n,{u,v}] gives the sequence starting with u,v, continuing up to at most n, where the general term is the least integer greater than the previous term that is expressible uniquely as the sum of two distinct earlier terms. |
Let u=1 and v=1. Call the sequence sn. Then s1=1 and s2=2 :
| In[1]:= |
| Out[1]= |
For term 3, there is only one sum, 3=1+2, so s3=3 :
| In[2]:= |
| Out[2]= |
For term 4, only the sum 1+3 gives 4, so s4=4. The sum 2+2 is not a sum of unique previous terms:
| In[3]:= |
| Out[3]= |
For term 5, the two sums 1+4 and 2+3 give 5, so s5≠ 5 . The sum 2+4 is 6; the sum 1+2+3=6 has more than one summand, so s5=6:
| In[4]:= |
| Out[4]= |
Here are the terms up to 1000:
| In[5]:= |
| Out[5]= |  |
The plot is wrinkly:
| In[6]:= |
| Out[6]= | 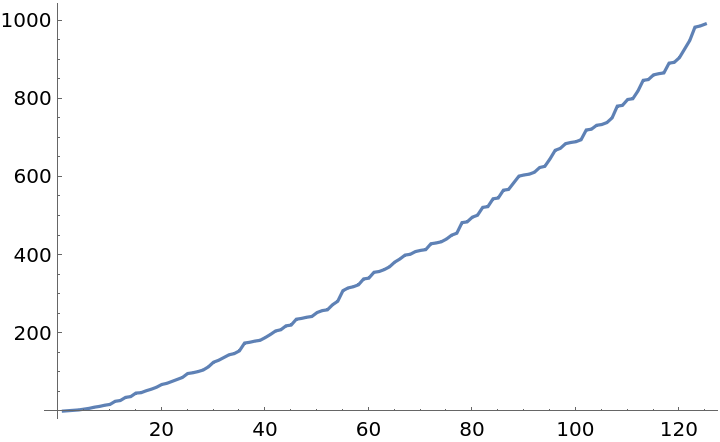 |
This sequence starts with 1, 3 instead of 1, 2:
| In[7]:= |
| Out[7]= |  |
More wrinkles:
| In[8]:= |
| Out[8]= | 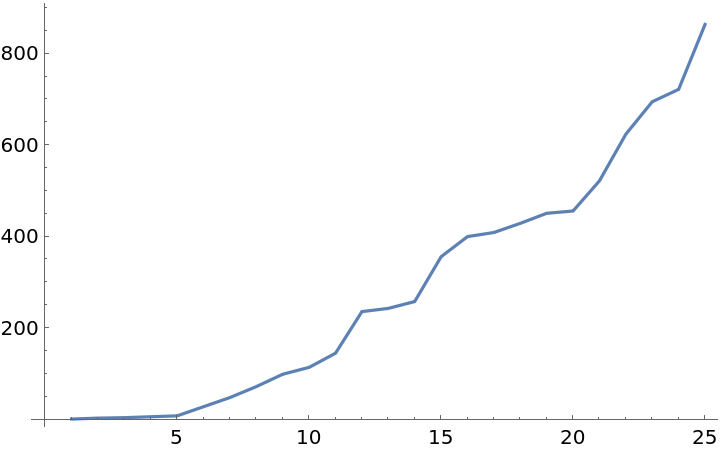 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License