Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a surface twisting a curve
ResourceFunction["TwistedSurface"][c,a,b,{u,v}] gives the parametric surface parameterized by variables u and v and generated by a generatrix curve c at a distance a from the origin, twisted b times. |
The Möbius strip is generated with a half twist:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 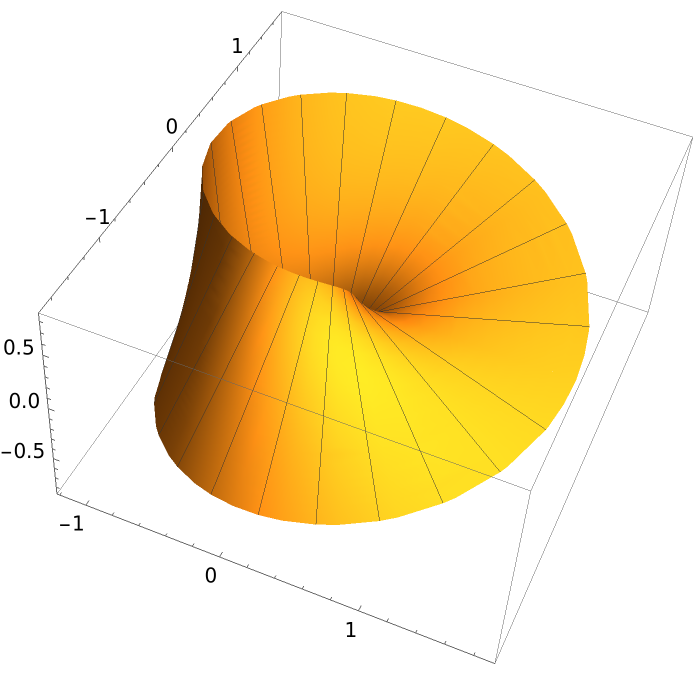 |
See how the surface is generated:
| In[3]:= | ![Manipulate[
ParametricPlot3D[
Evaluate[tms], {u, -2 \[Pi], uf}, {v, -\[Pi]/4, \[Pi]/4}, Mesh -> None, PlotRange -> {{-1.1, 1.8}, {-1.6, 1.6}, {-0.8, 0.8}}, PerformanceGoal -> "Quality"], {{uf, -\[Pi]}, -2 \[Pi] + .1, 0}]](https://www.wolframcloud.com/obj/resourcesystem/images/2d9/2d94dfcd-2b26-4d4d-94d5-98026067ce88/51dc7bdf61a8ed27.png) |
| Out[3]= |  |
Increase the distance from the origin:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= | 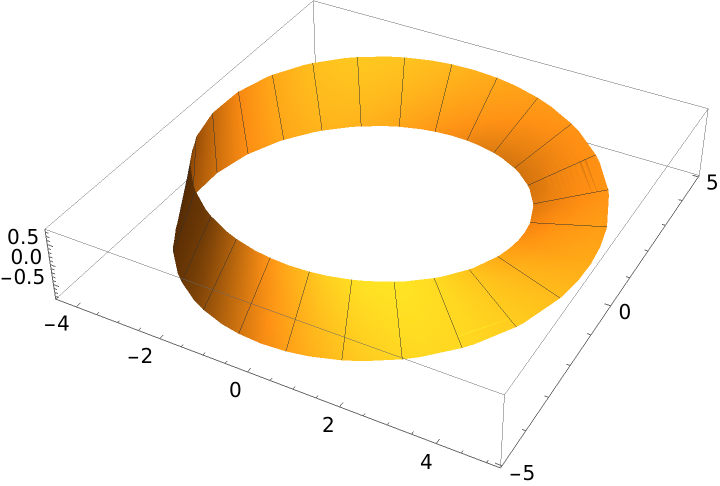 |
A complete twist:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= | 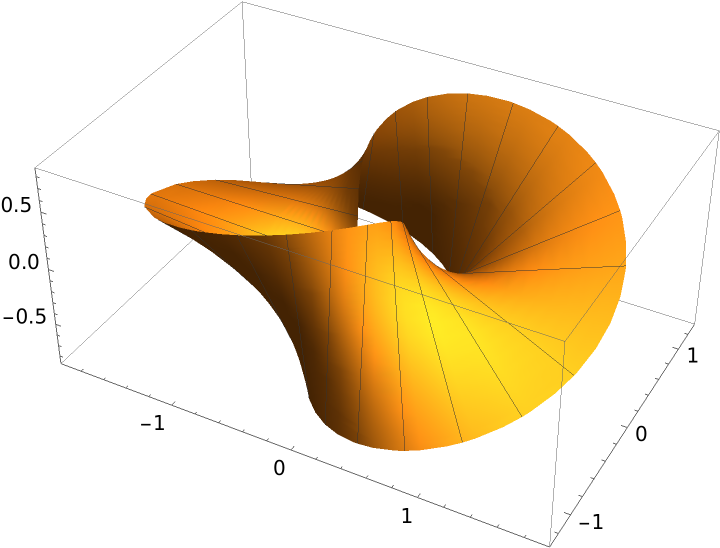 |
A lemniscate:
| In[8]:= |
| Out[8]= |
A twist of a lemniscate gives the figure–eight parametrization of a Klein bottle:
| In[9]:= | ![tlem = ResourceFunction["TwistedSurface"][
Entity["PlaneCurve", "Lemniscate"]["ParametricEquations"][1][u, v], 2, 1/2, {u, v}]](https://www.wolframcloud.com/obj/resourcesystem/images/2d9/2d94dfcd-2b26-4d4d-94d5-98026067ce88/53c31ea693ccda05.png) |
| Out[9]= | 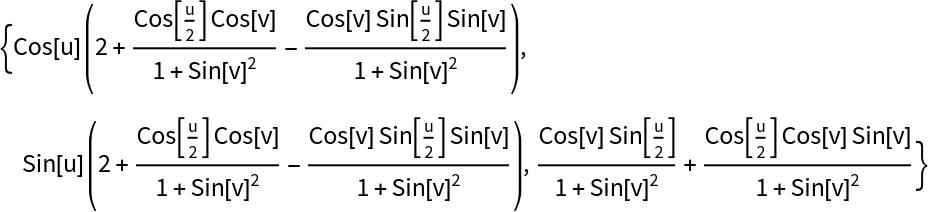 |
Plot the Klein bottle:
| In[10]:= |
| Out[10]= |  |
A Lissajous curve:
| In[11]:= |
A twist of the Lissajous curve:
| In[12]:= |
| Out[12]= | 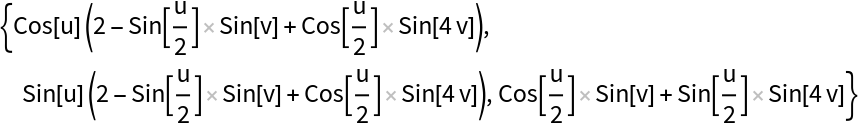 |
Plot the resulting surface:
| In[13]:= |
| Out[13]= | 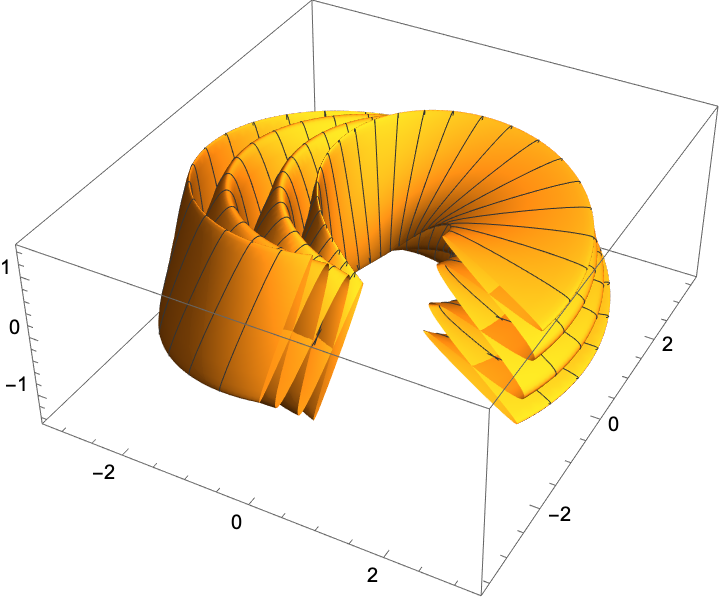 |
This work is licensed under a Creative Commons Attribution 4.0 International License