Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the turning number of a curve
ResourceFunction["TurningNumber"][c,{t,a,b}] computes the turning number of a curve c with parameter t running from a to b. |
The turning number changes its sign depending on whether the tangent vector moves clockwise or counterclockwise:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
Define a limaçon:
| In[3]:= |
| Out[3]= |
Here is a function for computing tangent vectors:
| In[4]:= | ![TangentVector[{f_, g_}, t_] := Module[{df = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]f\), dg = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]g\)}, {df, dg}/Sqrt[df^2 + dg^2]
]](https://www.wolframcloud.com/obj/resourcesystem/images/7c0/7c09efc1-e200-4570-baa9-d27261e5df60/60b4ef3bf2043686.png) |
Interactively plot the limaçon while tracking a tangent vector and its turning number. This shows that the turning number of a limaçon is 2:
| In[5]:= | ![Manipulate[
Show[ParametricPlot[limacon[3, 1][t], {t, 0, tf}, PlotRange -> {{-3, 5}, {-3, 3}}], Graphics[
Arrow[{limacon[3, 1][tf], limacon[3, 1][tf] + TangentVector[limacon[3, 1][t], t]}] /. t -> tf], PlotLabel -> ResourceFunction["TurningNumber"][
limacon[3, 1][t], {t, 0, tf}]], {{tf, \[Pi]}, .1, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/7c0/7c09efc1-e200-4570-baa9-d27261e5df60/4c15cf4249254bb6.png) |
| Out[5]= | 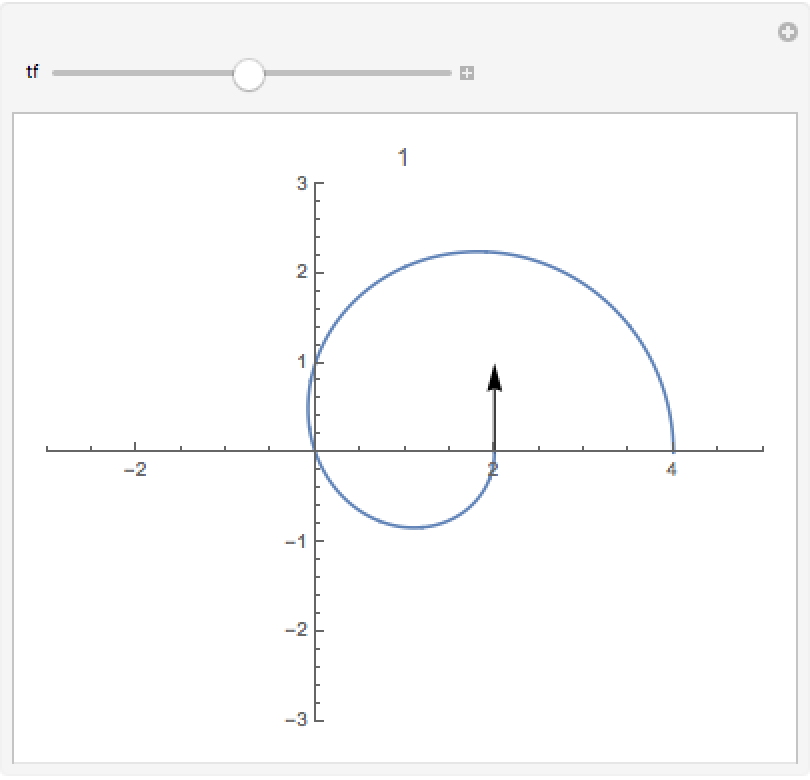 |
Define an eight curve:
| In[6]:= |
The turning number of an eight curve is first -1, then 1, giving a total of 0:
| In[7]:= | ![Manipulate[
Show[ParametricPlot[eight[t], {t, 0, tf}, PlotRange -> {{-1.1, 1.1}, {-1, 1}}], Graphics[
Arrow[{eight[tf], eight[tf] + .25 TangentVector[eight[t], t]}] /. t -> tf], PlotLabel -> ResourceFunction["TurningNumber"][
eight[t], {t, 0, tf}]], {{tf, \[Pi]}, .1, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/7c0/7c09efc1-e200-4570-baa9-d27261e5df60/14418b147daa278c.png) |
| Out[7]= | 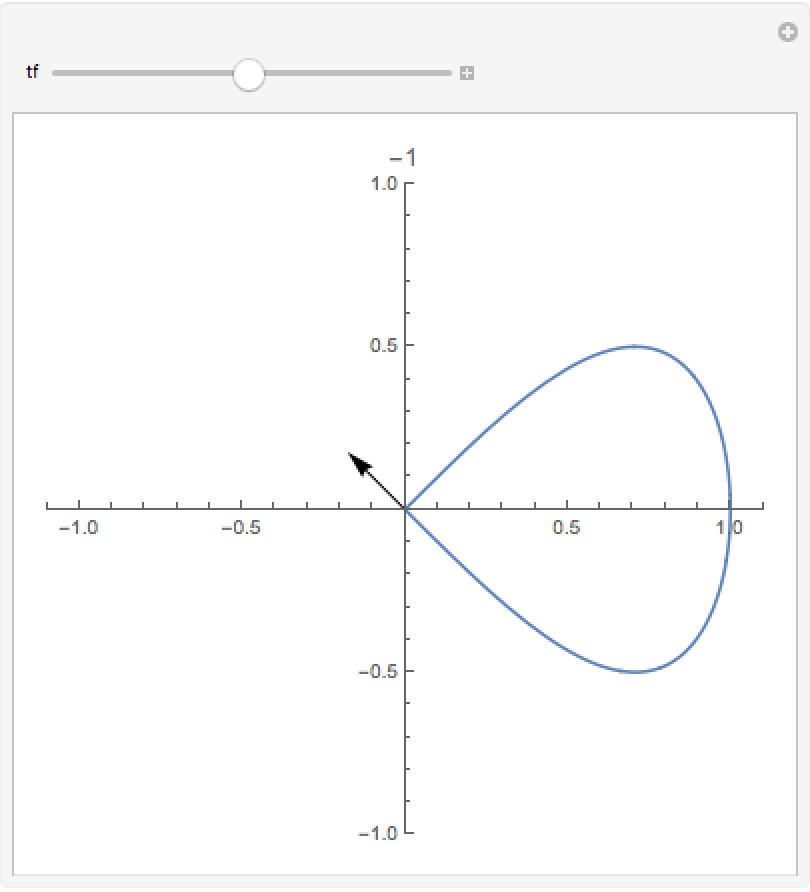 |
This work is licensed under a Creative Commons Attribution 4.0 International License