Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TuringMachineToNumber

Source Notebook

Convert an explicit list of rules into an enumerated Turing machine specification

Contributed by: Mano Namuduri

ResourceFunction["TuringMachineToNumber"][rules]

converts rules to an enumerated Turing machine specification containing the rule number, number of states and number of colors.

Details

The input rules should be a list of Rule or RuleDelayed elements of the form {si, ai} -> {sf, af, offset}, each of which contains Integer elements denoting the following:
siinitial state of the head
aiinitial value of the cell under the head
sffinal state of the head
affinal value of the cell under the head
offsetoffset by which the head moves
The output of ResourceFunction["TuringMachineToNumber"] is of the form {n, s, k}, with integer elements denoting the following:
nnumber encoding the given rules
snumber of states in the Turing machine
knumber of tape cell colors in the Turing machine
The number of possible Turing machine rules is as follows:
2-state, 2-color machines4096
s-state, k-color machines(2sk)^(sk)

Examples

Basic Examples (2) 

Convert a list of Turing machine rules into an enumerated specification:

In[1]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 1} -> {2, 0, -1}, {1, 0} -> {2, 1, 1}, {2, 1} -> {1, 0, 1}, {2, 0} -> {1, 1, -1}}]
Out[1]=

Show that the two specifications are equivalent:

In[2]:=
{RulePlot[ TuringMachine[{{1, 1} -> {2, 0, -1}, {1, 0} -> {2, 1, 1}, {2, 1} -> {1, 0, 1}, {2, 0} -> {1, 1, -1}}]], RulePlot[TuringMachine[{2506, 2, 2}]]}
Out[2]=

Scope (2) 

Generate all possible rules for a 1-state, 2-color Turing machine, ordered by rule number:

In[3]:=
rules = ResourceFunction["TuringMachineFromNumber"][#, 1, 2] & /@ Range[0, 15]
Out[3]=

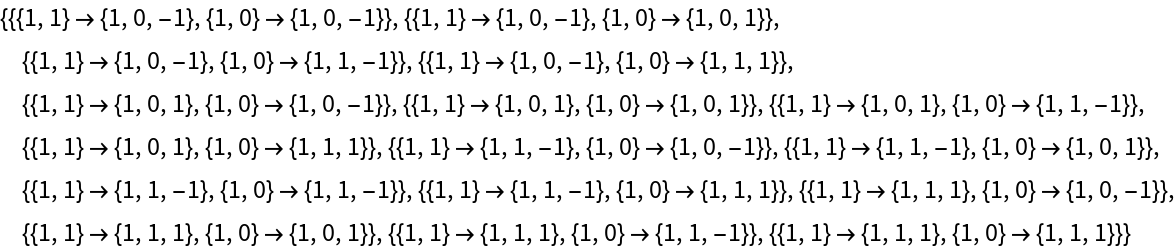
Convert the set of possible s = 1, k = 2 rules back to enumerated form:

In[4]:=
ResourceFunction["TuringMachineToNumber"] /@ rules
Out[4]=

Possible Issues (3) 

In a valid Turing machine specification, head states must be integers greater than 0:

In[5]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 0} -> {0, 0, -1}, {2, 0} -> {0, 0, -1}}]
Out[5]=

In a valid Turing machine specification, tape colors must be integers greater than or equal to 0:

In[6]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 0} -> {1, -1, -1}, {2, 0} -> {1, -1, -1}}]
Out[6]=

TuringMachineToNumber cannot accept offsets with the head List:

In[7]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 0} -> {1, 0, {-1, -1}}, {2, 0} -> {1, 0, {-1, -1}}}]
Out[7]=

TuringMachineToNumber cannot accept offsets that are not 1 or -1:

In[8]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 0} -> {1, 0, -2}, {2, 0} -> {1, 0, -2}}]
Out[8]=

Turing machines that have multiple transformations for a single input configuration cannot be enumerated:

In[9]:=
ResourceFunction[ "TuringMachineToNumber"][{{1, 0} -> {1, 0, -1}, {1, 0} -> {1, 0, -1}}]
Out[9]=

Turing machines that do not have a transformation for every possible input configuration cannot be enumerated:

In[10]:=
ResourceFunction["TuringMachineToNumber"][{{2, 0} -> {1, 0, -1}}]
Out[10]=

Version History

  • 1.0.0 – 12 April 2021

Related Resources

Author Notes

In the future, this function could be extended to accept non-unit offsets. In this case, it could return the rule format {n, s, k, {{off1}, {off2}, …}}, which explicitly gives the offset for each rule and is a format currently accepted by TuringMachine.

License Information