Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TsallisEntropy

Source Notebook

Compute the Tsallis entropy

Contributed by: Julián Laverde and Mads Bahrami

ResourceFunction["TsallisEntropy"][prob,q,k]

returns the Tsallis entropy for a list of discrete associated probablities prob of the possible configurations for the entropic index q and constant k.

ResourceFunction["TsallisEntropy"][dist,q,k]

returns the Tsallis entropy of the probability distribution dist, entropic index q and constant k.

ResourceFunction["TsallisEntropy"]["formula"]

returns the specified formula of the Tsallis entropy.

Details

Tsallis entropy is a generalization of the Boltzmann–Gibbs–Shannon entropy.
For a discrete set of probabilities {pi}, the Tsallis entropy is defined as .
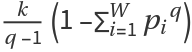
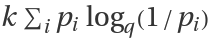
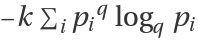
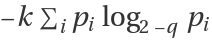
Tsallis entropy Sq can equivalently be written as , or , or , where the q-logarithm logqz is defined as logqz=(z1-q-1)/(1-q), with log1z= log z being the limiting value as q→1.
For a continuous probability distribution p(x), the Tsallis entropy is defined as .
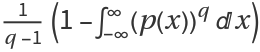
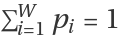
ResourceFunction["TsallisEntropy"][prob,q,k] computes the Tsallis entropy for a given discrete set of probabilities prob={pi} with the condition , where W=Length[prob] is the number of possible configurations. If prob is not normalized, it will be normalized first.
In the limit as q→1 for ResourceFunction["TsallisEntropy"][…], the Shannon differential entropy is recovered.
In ResourceFunction["TsallisEntropy"][prob,q,k], prob can be a list of real numbers. q and k can be real numbers.
In ResourceFunction["TsallisEntropy"][dist,q,k], dist can be any built-in continuous or discrete distribution in the Wolfram Language, or a mixture of them.
If not given, the default value of k is 1.
In ResourceFunction["TsallisEntropy"]["formula"], "formula" can be any of the following:
"DiscreteFormula"formula for Tsallis entropy for a discrete set of probabilities
"ContinuousFormula"formula for Tsallis entropy for a continuous probability distribution

Examples

Basic Examples (3) 

Compute the Tsallis entropy for a discrete set of probabilities from a list:

In[1]:=
ResourceFunction["TsallisEntropy"][{0.2, 0.3, 0.5}, 2, 1]
Out[1]=

The Tsallis entropy for a built-in discrete probability distribution:

In[2]:=
ResourceFunction["TsallisEntropy"][ZipfDistribution[1], 2, 1]
Out[2]=

The Tsallis entropy for a continuous probability distribution:

In[3]:=
ResourceFunction["TsallisEntropy"][ TsallisQGaussianDistribution[2, .5, 1.5], 2]
Out[3]=

Scope (2) 

The formula for the Tsallis entropy of a discrete set of probabilities:

In[4]:=
ResourceFunction["TsallisEntropy"]["DiscreteFormula"]
Out[4]=

The formula for the Tsallis entropy of a continuous probability distribution:

In[5]:=
ResourceFunction["TsallisEntropy"]["ContinuousFormula"]
Out[5]=

Possible Issues (1) 

In TsallisEntropy[prob,q,k], all elements of the list prob must be positive:

In[6]:=
ResourceFunction["TsallisEntropy"][{-0.2, 0.3, 0.5}, 2, 1]
Out[6]=

Neat Examples (4) 

Tsallis entropy is concave for q>0, and convex for q<0. Plot Sq/k versus p:

In[7]:=
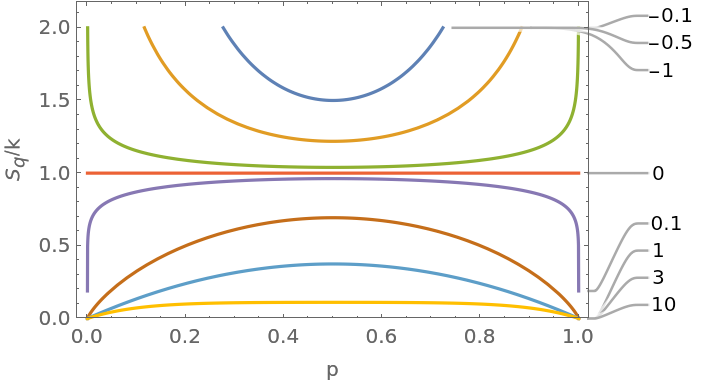
Sq[p_] := Table[ResourceFunction["TsallisEntropy"][{p, 1 - p}, q, 1], {q, values = {-1, -0.5, -.1, 0, 0.1, 1, 3, 10}}]; Plot[Evaluate@Sq[p], {p, 0, 1}, PlotRange -> {0, 2}, FrameLabel -> {"p", "\!\(\*SubscriptBox[\(S\), \(q\)]\)/k"}, Frame -> True, PlotLabels -> values]
Out[7]=

Plot the value of the Tsallis entropy at its extremum (equiprobability) for k=1 and typical values of q:

In[8]:=
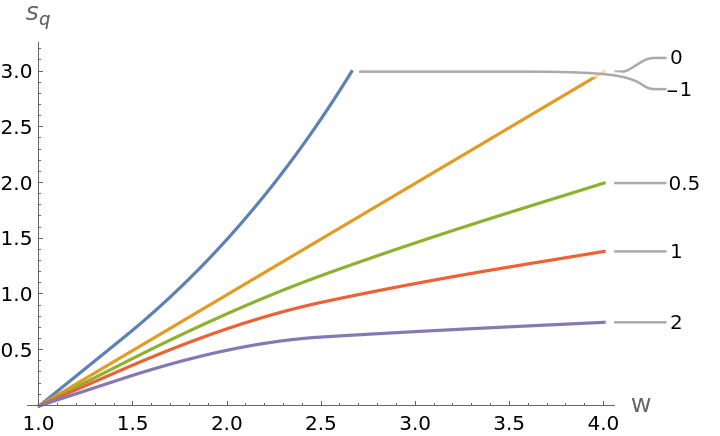
ListPlot[Table[ ResourceFunction["TsallisEntropy"][Table[1/W, {x, 1, W}], q, 1], {q, {-1, 0, 0.5, 1, 2}}, {W, 1, 4}], Joined -> True, AxesOrigin -> {1, 0}, PlotRange -> {0, 3}, PlotLabels -> {-1, 0, 0.5, 1, 2}, InterpolationOrder -> 2, AxesLabel -> {"W", "\!\(\*SubscriptBox[\(S\), \(q\)]\)"}]
Out[8]=

Show non-additivity Sq(A,B)=Sq(A)+Sq(B)+(1-q)Sq(A)Sq(B) for two independent systems A and B with discrete sets of probability:

In[9]:=
q = 2; p1 = {0.2, 0.3, 0.5}; p2 = {0.1, 0.6, 0.3}; ResourceFunction["TsallisEntropy"][Flatten@Outer[Times, p1, p2], q, 1] == ResourceFunction["TsallisEntropy"][p1, q, 1] + ResourceFunction["TsallisEntropy"][p2, q, 1] + (1 - q) ResourceFunction["TsallisEntropy"][p1, q, 1]* ResourceFunction["TsallisEntropy"][p2, q, 1]
Out[9]=

Show non-additivity Sq(A,B)=Sq(A)+Sq(B) with q=1 for two independent systems A and B with continuous probability distributions:

In[10]:=
q = 1; \[ScriptCapitalD]1 = NormalDistribution[0, 2]; \[ScriptCapitalD]2 = NormalDistribution[1/3, 1]; ResourceFunction["TsallisEntropy"][ ProductDistribution[\[ScriptCapitalD]1, \[ScriptCapitalD]2], q] == ResourceFunction["TsallisEntropy"][\[ScriptCapitalD]1, q] + ResourceFunction["TsallisEntropy"][\[ScriptCapitalD]2, q]
Out[10]=

Publisher

WolframSpecialProjects

Version History

  • 1.1.0 – 12 April 2021
  • 1.0.0 – 23 March 2021

Source Metadata

  • Citation:
    • Tsallis, C., "Possible generalization of Boltzmann-Gibbs statistics." Journal of Statistical Physics, vol. 52, nos. 1–2, 479–487, 1988. DOI: 10.1007/bf01016429

Related Resources

License Information