Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Generate a truth table for a Boolean expression
ResourceFunction["TruthTable"][expr,vars] creates a truth table for the logical expression expr with respect to vars. |
Produce a truth table for a simple logical expression:
| In[1]:= |
| Out[1]= | 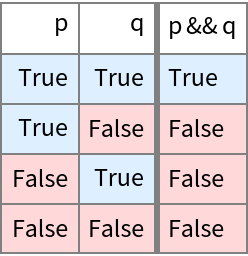 |
You can also build up larger expressions:
| In[2]:= |
| Out[2]= | 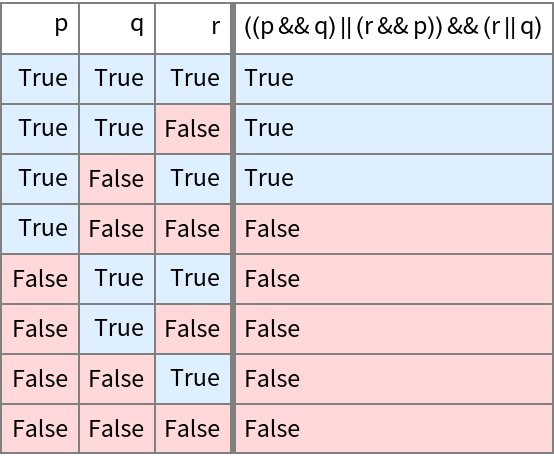 |
TruthTable also accepts raw BooleanFunction inputs and produces an explicit logical expression for the function:
| In[3]:= |
| Out[3]= |  |
Display the same result using the list format:
| In[4]:= |
| Out[4]= |
Show DeMorgan's law by comparing two logical expressions:
| In[5]:= |
| Out[5]= | 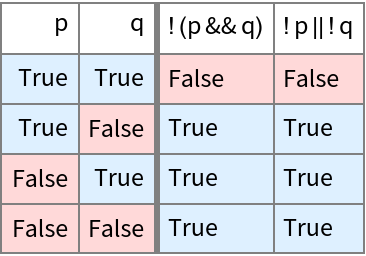 |
Show that Implies is not associative by comparing the truth tables of two expressions:
| In[6]:= |
| Out[6]= | 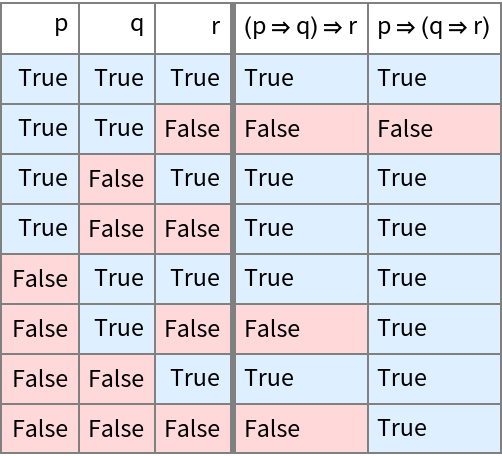 |
Use a truth table to easily determine if multiple logical expressions are equivalent:
| In[7]:= |
| Out[7]= | 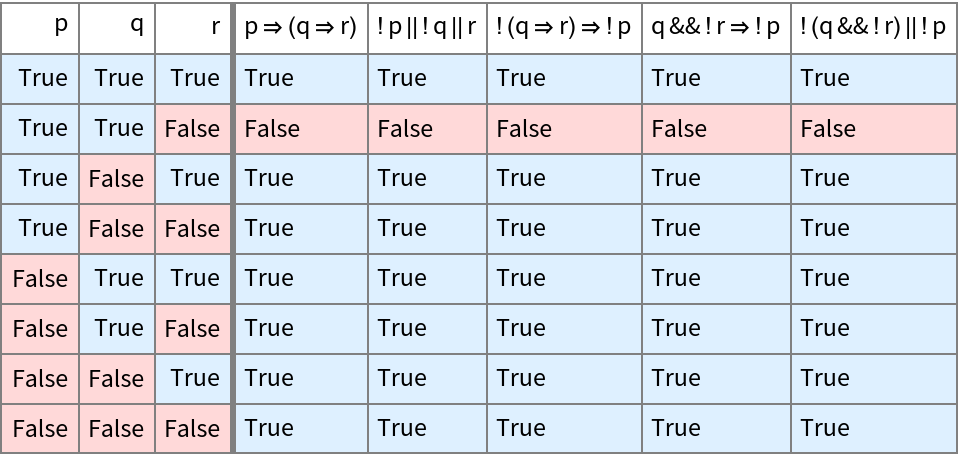 |
This work is licensed under a Creative Commons Attribution 4.0 International License