Basic Examples (1) 

Generate a dataset for the Sin function:

In[1]:=

Out[1]=

Scope (5) 

Generate some trigonometric data:

In[2]:=

Show all information for a specified row:

In[3]:=

Out[3]=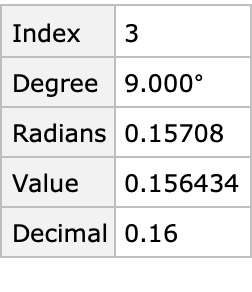

Select one of the columns in this row to show the result in standard closed form:

In[4]:=

Out[4]=

Show the entire row outside of the dataset with StandardForm:

In[5]:=

Out[5]=

The same thing can be gotten by applying Normal:

In[6]:=

Out[6]=

Options (5) 

With the "Digits" option, one can get any precision value for the results in the "Decimal" column:

In[7]:=

Out[7]=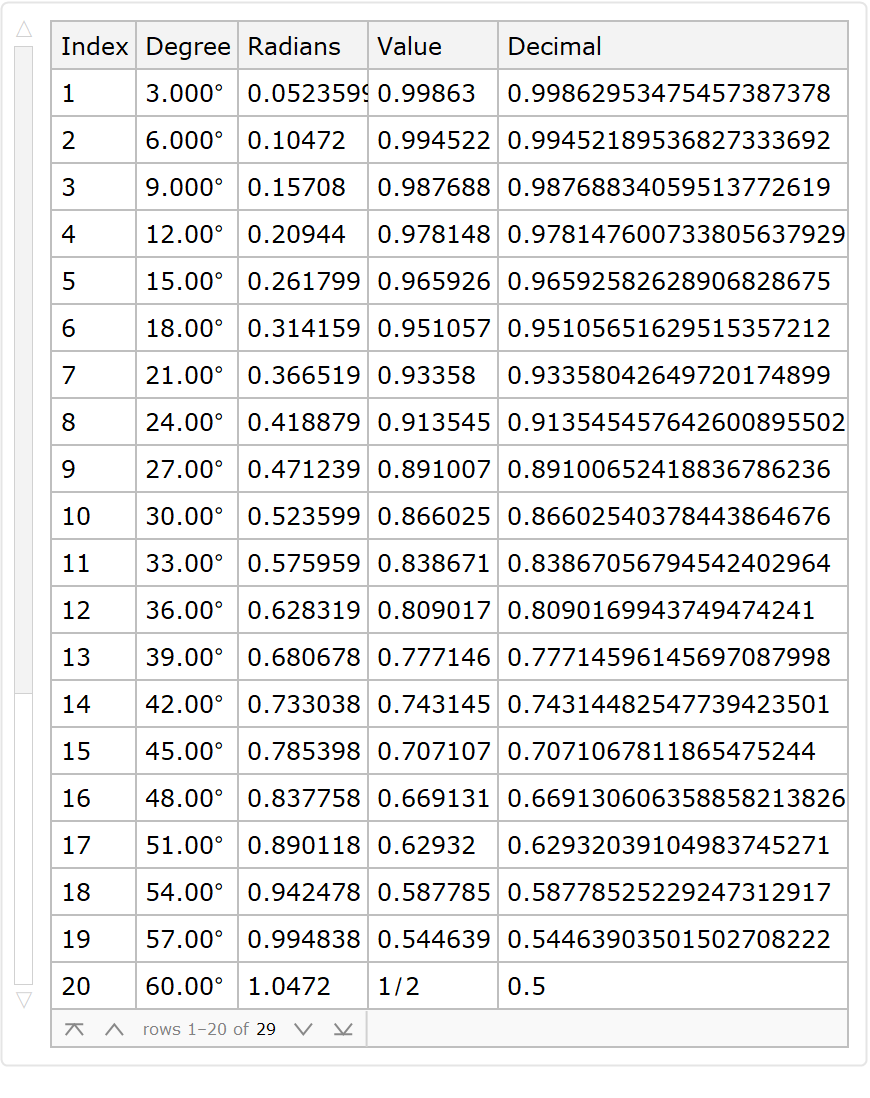

Use the option "DegreeStep" to specify the difference between the angle at successive rows in the results. Values which are multiples of 1/8 will give results in terms of radicals:

In[8]:=

Out[8]=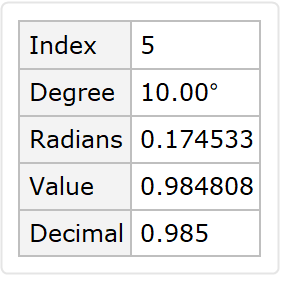

In[9]:=

Out[9]=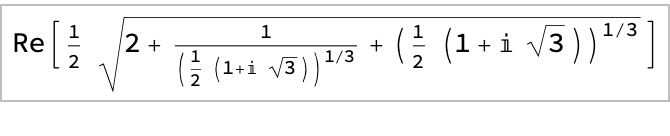

Use 12 degree steps:

In[10]:=

Out[10]=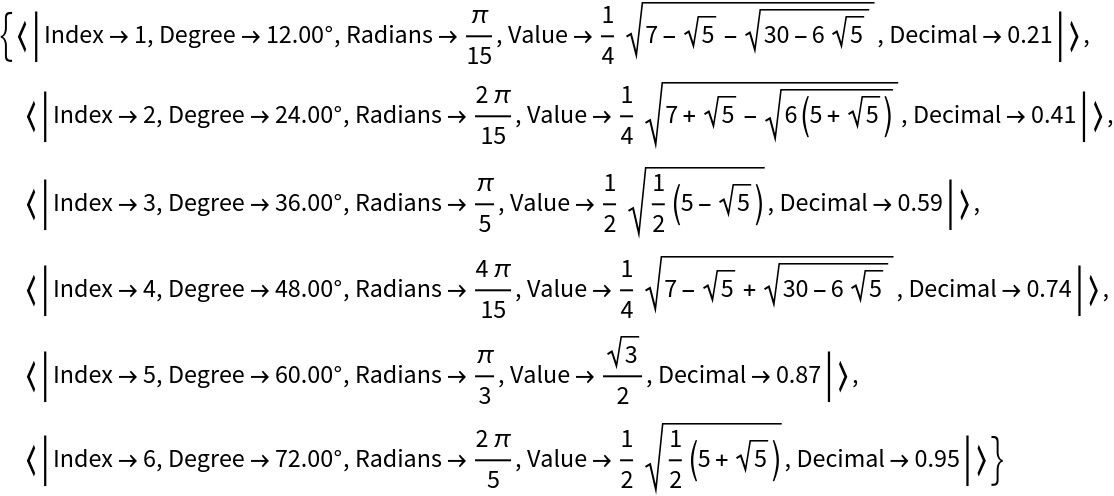

Show multiple results simultaneously:

In[11]:=

In[12]:=

Out[12]=

For many "DegreeStep" values, one can obtain a radical result using "Value":

In[13]:=

Out[13]=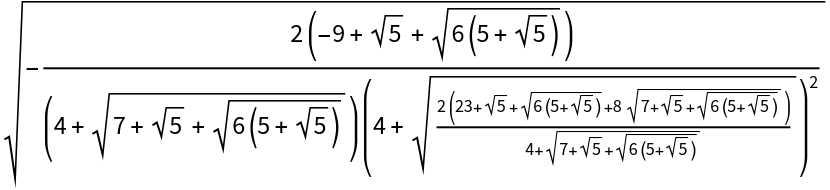

Use a Quantity for "DegreeStep" to specify radians:

In[14]:=

Out[14]=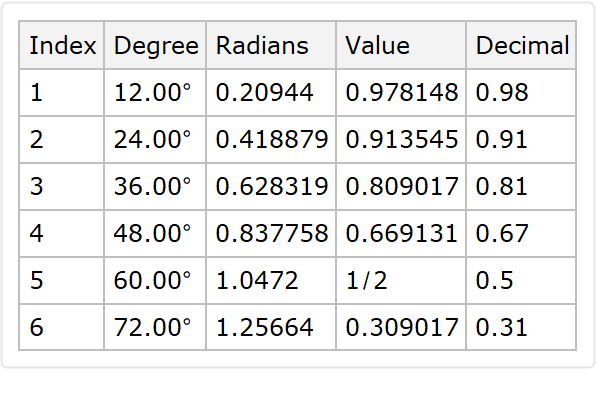

In[15]:=

Out[15]=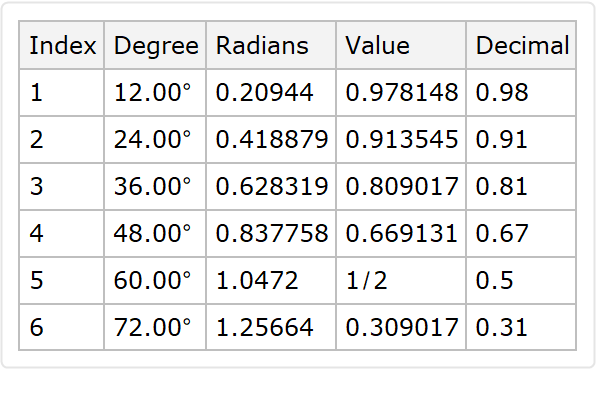

Possible Issues (2) 

Sometimes the result of the closed form appears inside the dataset, which is not very useful for copying the result:

In[16]:=

Out[17]=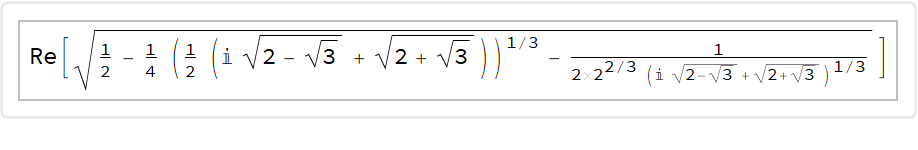

Retrieve the StandardForm:

In[18]:=

Out[18]=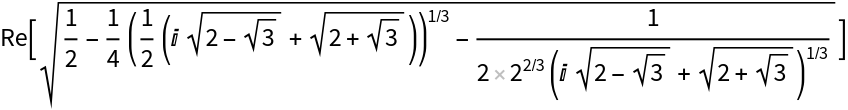

The smaller the "DegreeStep", the longer the time to evaluate. Tangent with step 1/2 takes about 10 minutes and step 3/8 takes about 20 minutes:

In[19]:=

Out[19]=

In[20]:=

Out[20]=