Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 Triangle3DTo2D

Source Notebook

Given a 3D triangle, return an equivalent 2D triangle along with a transformation function

Contributed by: Ed Pegg Jr

Triangle3Dto2D[triangle]

computes a two-dimensional triangle along with a rotation matrix and offset vector so that one can recover triangle given in three-dimensional space.

Triangle3Dto2D[triangle,"TransformationFunction"]

computes a two-dimensional triangle along with a TransformationFunction so that one can recover triangle given in three-dimensional space.

Examples

Basic Examples (2) 

Given a 3D triangle, generate a 2D triangle, a matrix and an offset:

In[1]:=
triangle3D = {{1, -1, 1}, {-2, 3, 0}, {1, -1, 2}}; {tri, mat, off} = ResourceFunction["Triangle3DTo2D"][triangle3D]
Out[1]=

Calculate some results in 2D, then return to 3D:

In[2]:=
results2D = Join[tri, {Circumsphere[tri][[1]], Mean[tri]}]; Simplify[# + off & /@ ((Append[#, 0] & /@ results2D) . mat)]
Out[2]=

Scope (2) 

Generate a 2D triangle and a transformation function from a 3D triangle:

In[3]:=
triangle3D = {{1, -1, 1}, {-2, 3, 0}, {1, -1, 2}}; {tri, tf} = ResourceFunction["Triangle3DTo2D"][triangle3D, "TransformationFunction"]
Out[3]=

Calculate some results in 2D, then return to 3D:

In[4]:=
results2D = Join[tri, {Circumsphere[tri][[1]], Mean[tri]}]; Simplify[ tf[Append[#, 0] & /@ results2D]]
Out[4]=

The matrix and offset can be discarded:

In[5]:=
triangle3D = RandomInteger[{-9, 9}, {3, 3}] triangle2D = ResourceFunction["Triangle3DTo2D"][triangle3D][[1]]
Out[5]=
Out[6]=

Show both triangles in a 3D graphic:

In[7]:=
Graphics3D[{Polygon[triangle3D], Polygon[Append[#, 0] & /@ triangle2D]}]
Out[7]=

Neat Examples (3) 

Find triangles of a polyhedron:

In[8]:=
polytris = First /@ PolyhedronData["TriakisTetrahedron", "Polygons"];

Look at the 2D triangle for one of them:

In[9]:=
RootReduce[ResourceFunction["Triangle3DTo2D"][polytris[[1]]][[1]]]
Out[9]=

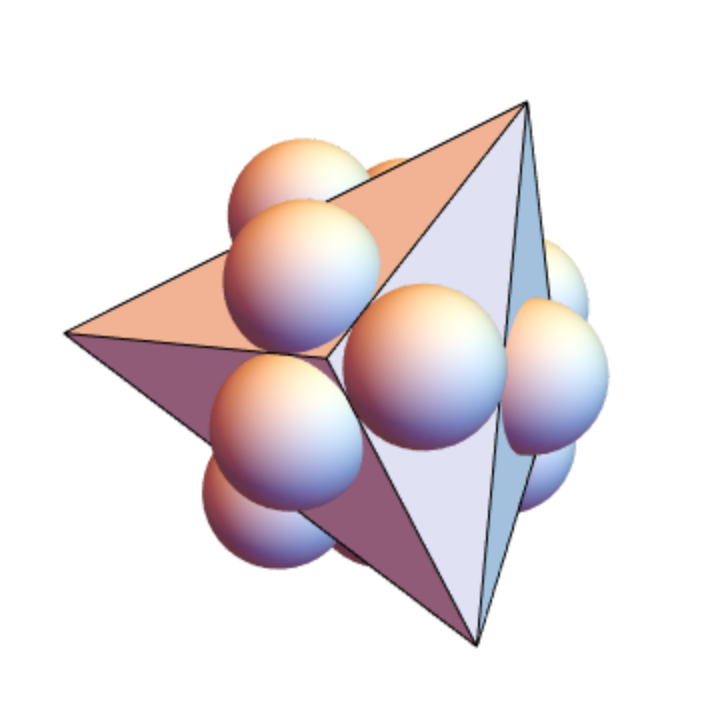
Draw tangent spheres on each triangle:

In[10]:=
centers = Table[{tri, tf} = ResourceFunction["Triangle3DTo2D"][polytris[[n]], "TransformationFunction"]; results2D = {Insphere[tri][[1]]}; Simplify[tf[PadRight[results2D, {Automatic, 3}]]], {n, 1, 12}]; Graphics3D[{Polygon[polytris], Sphere[Flatten[centers, 1], 5/(6 Sqrt[11])]}, Boxed -> False, SphericalRegion -> True, ViewAngle -> Pi/8]
Out[10]=

Version History

  • 1.1.0 – 14 June 2021
  • 1.0.0 – 21 October 2019

License Information