Function Repository Resource:

TransversalHypergraph

Compute the transversal hypergraph of a hypergraph defined by a list of hyperedges and isolated vertices

Contributed by: Daniel McDonald

ResourceFunction["TransversalHypergraph"][list]

computes the transversal hypergraph of list.

Details and Options

The hypergraph represented by {{v₁₁,v₁₂,…},{v₂₁,v₂₂,…},…,u₁,u₂,…} has vertices v₁₁,v₁₂,…,v₂₁,v₂₂,…,…,u₁,u₂,… and hyperedges {v₁₁,v₁₂,…},{v₂₁,v₂₂,…},….

Given a hypergraph H having sets V and E of vertices and hyperedges, a transversal T of H is a subset U of V that has a non-empty intersection with each hyperedge in E; a minimal transversal is a transversal containing no other transversal as a proper subset. The transversal hypergraph Tr(H) of H is the hypergraph whose hyperedges are the minimal transversals of H.

Examples

Basic Examples (1)

Compute the transversal hypergraph of the hypergraph having vertices a, b, c, d, e, f, g and hyperedges {a,b,c,d}, {b,c}, {c,d,e}:

In[1]:=

Out[1]=

Applications (4)

Define a random hypergraph having n vertices and m hyperedges:

In[2]:=

$RandomHypergraph[n_, m_] := With[{edges = Apply[Join, Map[Function[pos, Subsets[Range[n], {1, n}, {pos}]], RandomInteger[{1, 2^n - 1}, m]]]}, Join[edges, Complement[Range[n], Flatten[edges]]]] rh = RandomHypergraph[15, 3]$

Out[3]=

Plot the hypergraph:

In[4]:=

$HypergraphPlot[hyp_List] := CommunityGraphPlot[ Graph[DeleteDuplicates[Flatten[hyp, 1]], {}, VertexLabels -> "Name"], Select[hyp, ListQ], CommunityRegionStyle -> Apply[Function[{r, g, b}, RGBColor[r, g, b, .5]], Most[Tuples[{0, 1}, 3]], {1}]] HypergraphPlot[rh]$

Out[5]=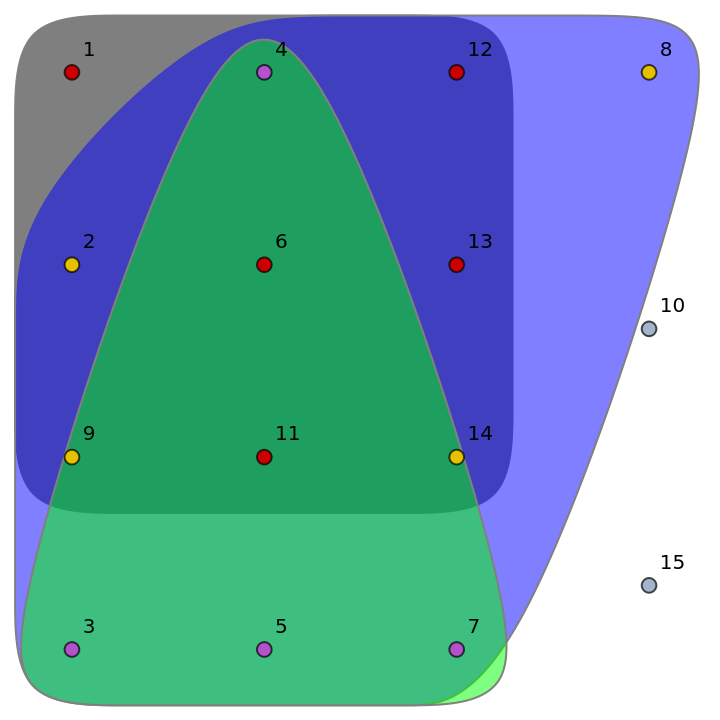

Find its transversal hypergraph:

In[6]:=

Out[6]=

Plot the transversal hypergraph:

In[7]:=

Out[7]=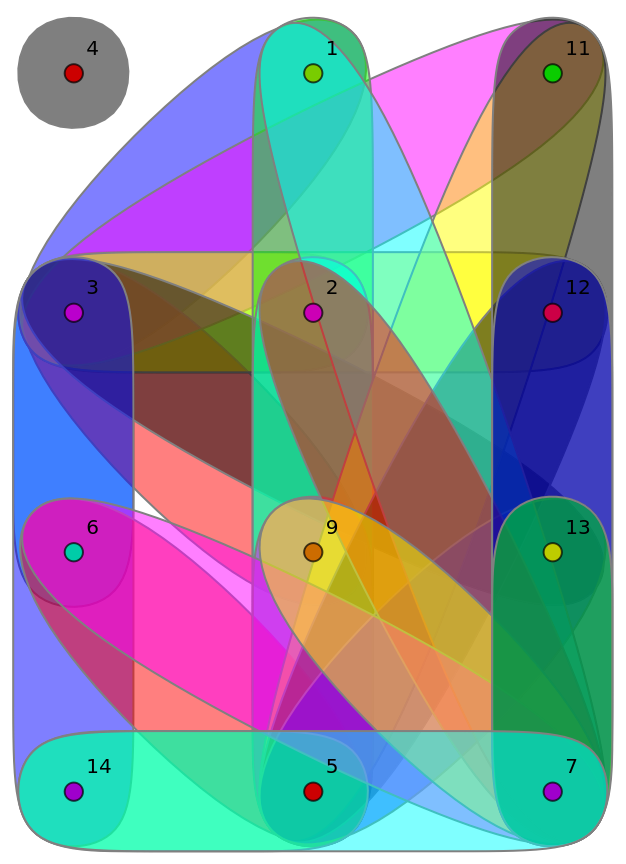

Publisher

Daniel McDonald

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

1.0.0 – 16 January 2019

Source Metadata

Citation:
- Kavvadias, D. J., Stavropoulos, E. C., "An Efficient Algorithm for the Transversal Hypergraph Generation." J. Graph Algorithms Appl., vol. 9, no. 2, 239-264, 2005. DOI: 10.7155/jgaa.00107. http://emis.muni.cz/journals/JGAA/accepted/2005/KavvadiasStavropoulos2005.9.2.pdf

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository