Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Transfinite interpolation of functions representing boundary curves of a surface
ResourceFunction["TransfiniteInterpolation"][{fs,fn},{fw,fe},{x,xmin,xmax},{y,ymin,ymax}] gives the transfinite interpolation of the functions fw and fe over x and the functions fs and fn over y. |
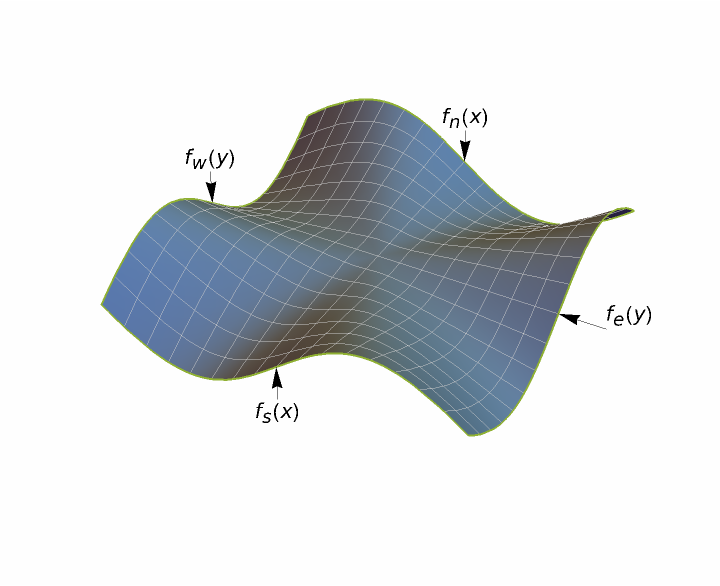
Build the transfinite interpolant of a given set of slice functions:
| In[1]:= |
| Out[1]= |
Plot the transfinite interpolant:
| In[2]:= |
| Out[2]= | 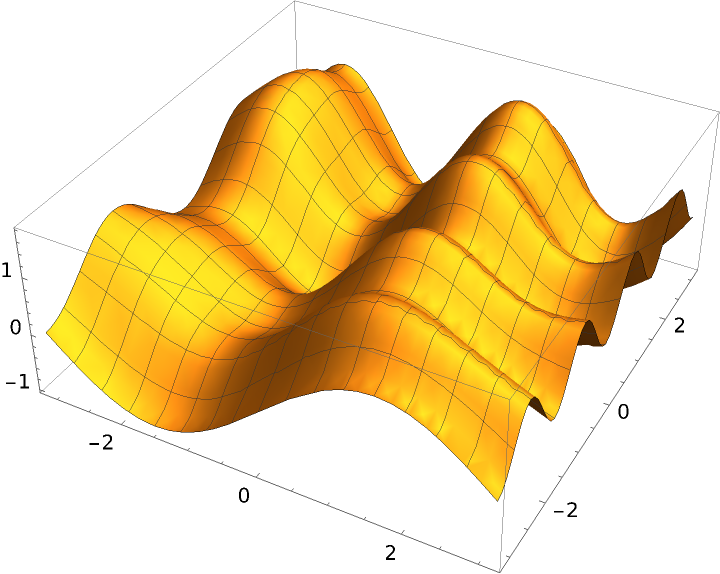 |
Construct a transfinite interpolant:
| In[3]:= |
| Out[3]= |
Construct another interpolant by solving a Laplace equation:
| In[4]:= |
| Out[4]= |
Compare the two interpolating functions:
| In[5]:= |
| Out[5]= | 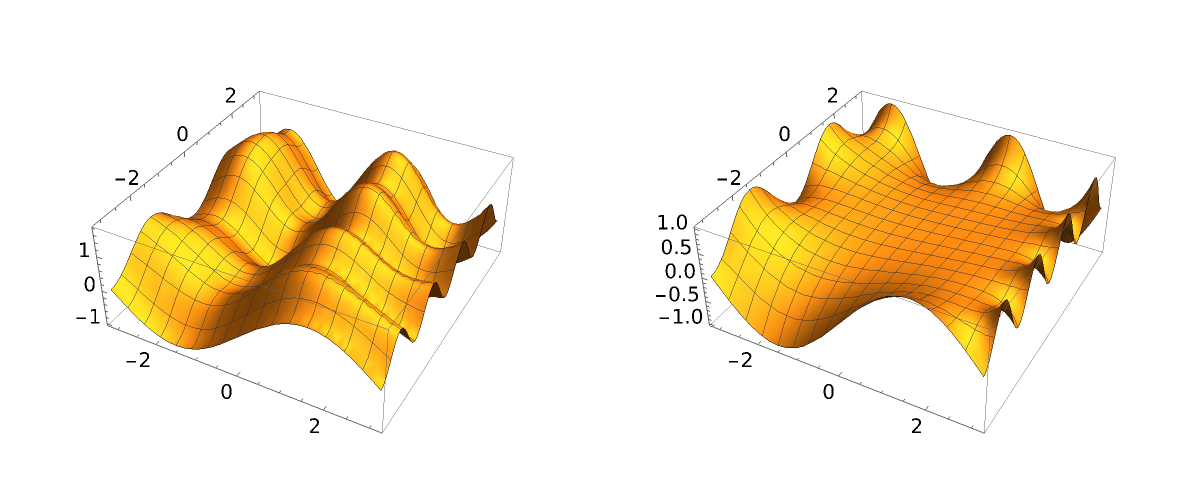 |
The two functions agree at the boundaries, but behave differently within them:
| In[6]:= |
| Out[6]= | 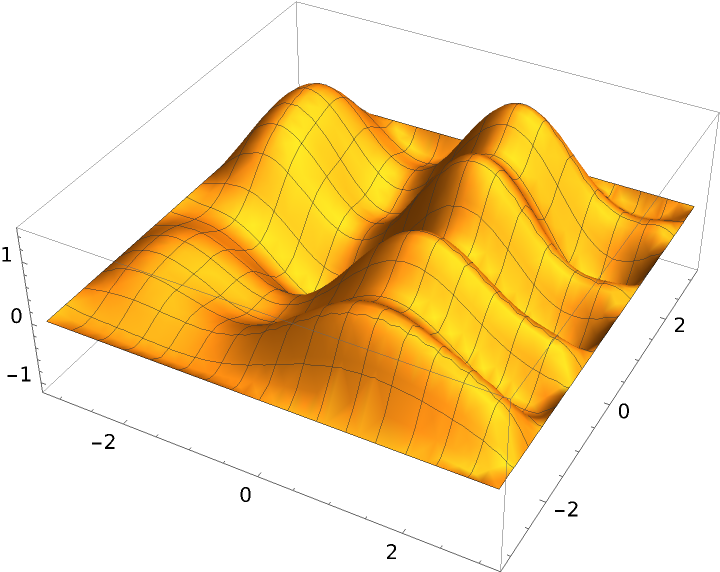 |
This work is licensed under a Creative Commons Attribution 4.0 International License