Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TracySinghProduct

Source Notebook

Calculate the Tracy–Singh product of two matrices

Contributed by: Jan Mangaldan

ResourceFunction["TracySinghProduct"][m1,m2,{r1,c1},{r2,c2}]

gives the Tracy-Singh product of m1 and m2, where the ri and ci are corresponding integer partitions of the dimensions of the mi.

Details

If m1 has dimensions p1×q1, then r1 and c1 must both be vectors with positive integer components that respectively sum top1 and q1, and similarly for m2.
ResourceFunction["TracySinghProduct"] can be used on SparseArray objects, returning a SparseArray object when possible.

Examples

Basic Examples (1) 

The Tracy-Singh product of two partitioned matrices:

In[1]:=
ResourceFunction["TracySinghProduct"][( { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} } ), \!\(\* TagBox[ RowBox[{"(", "", GridBox[{ {"1", "4", "7"}, {"2", "5", "8"}, {"3", "6", "9"} }, GridBoxAlignment->{"Columns" -> {{Center}}, "Rows" -> {{Baseline}}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\), {{2, 1}, {2, 1}}, {{1, 2}, {1, 2}}] // MatrixForm
Out[1]=

Scope (2) 

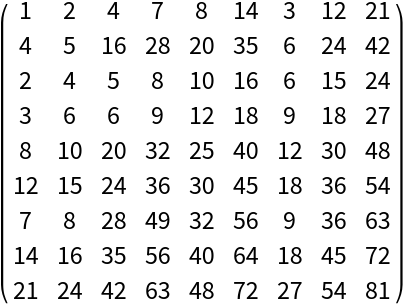The Tracy-Singh product of two rectangular matrices with symbolic entries:

In[2]:=
ResourceFunction["TracySinghProduct"][Array[\[FormalX], {5, 4}], Array[\[FormalY], {2, 3}], {{2, 1, 2}, {1, 3}}, {{1, 1}, {1, 2}}]
Out[2]=

The Tracy-Singh product of two sparse matrices:

In[3]:=
s = SparseArray[{i_, i_} :> i, {3, 3}]; t = SparseArray[{{i_, j_} /; Abs[i - j] == 1 :> i - j}, {4, 4}]; ResourceFunction[ "TracySinghProduct"][s, t, {{1, 2}, {2, 1}}, {{3, 1}, {2, 2}}]
Out[3]=

Properties and Relations (2) 

The Kronecker product is a special case of the Tracy-Singh product:

In[4]:=
ResourceFunction["TracySinghProduct"][m1, m2, ConstantArray[1, #] & /@ Dimensions[m1], Transpose[{Dimensions[m2]}]] == KroneckerProduct[m1, m2]
Out[4]=
In[5]:=
ResourceFunction["TracySinghProduct"][m1, m2, Transpose[{Dimensions[m1]}], ConstantArray[1, #] & /@ Dimensions[m2]] == KroneckerProduct[m2, m1]
Out[5]=

The Tracy-Singh product is effectively the pairwise Kronecker product for each pair of partitions in the two matrices:

In[6]:=
m1 = Array[\[FormalX], {5, 4}]; m2 = Array[\[FormalY], {2, 3}]; ResourceFunction["TracySinghProduct"][m1, m2, {{3, 2}, {2, 2}}, {{1, 1}, {1, 2}}] == tracySinghDef[m1, m2, {{3, 2}, {2, 2}}, {{1, 1}, {1, 2}}]
Out[6]=

Version History

  • 1.0.0 – 19 August 2022

Source Metadata

  • Citation:
    • Tracy D.S., Jinadasa K.G., "Partitioned Kronecker products of matrices and applications." Canadian Journal of Statistics, vol. 17, no. 1, 107-120, 1989.
      DOI: 10.2307/3314768
    • Tracy D.S., Singh R.P., "A new matrix product and its applications in partitioned matrix differentiation."Statistica Neerlandica, vol. 26, no. 4, 143-157, 1972.
      DOI: 10.1111/j.1467-9574.1972.tb00199.x

Related Resources

License Information