Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 TotalSignedCurvature

Source Notebook

Compute the total signed curvature of a curve

Contributed by: Wolfram Staff (original content by Alfred Gray)

ResourceFunction["TotalSignedCurvature"][c,t]

computes the total signed curvature of a curve c with respect to parameter t.

ResourceFunction["TotalSignedCurvature"][c,{t,a,b}]

computes the total signed curvature from a to b.

Details and Options

The signed curvature κ of a plane curve c is defined as , and measures the bending of the curve at each of its points. A measure of the total bending of c is given by .

Examples

Basic Examples (4) 

Compute the total signed curvature of a circle:

In[1]:=
ResourceFunction["TotalSignedCurvature"][ Entity["PlaneCurve", "Circle"]["ParametricEquations"][a][t], {t, a, b}]
Out[2]=

Some results are very similar:

In[3]:=
{#, ResourceFunction[ "TotalSignedCurvature"][#["ParametricEquations"][a, b][t], {t, a, b}]} & /@ {Entity["PlaneCurve", "LogarithmicSpiral"], Entity["PlaneCurve", "Cardioid"], Entity["PlaneCurve", "Nephroid"], Entity["PlaneCurve", "Deltoid"], Entity["PlaneCurve", "Cycloid"]} // Grid
Out[3]=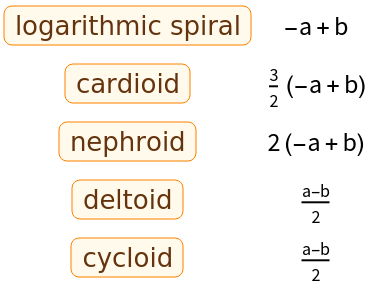

Some results involve inverse functions:

In[4]:=
ResourceFunction[ "TotalSignedCurvature"][#["ParametricEquations"][a][t], t] & /@ {Entity["PlaneCurve", "Catenary"], Entity["PlaneCurve", "Lemniscate"], Entity["PlaneCurve", "AgnesiWitch"]}
Out[4]=

Find the result for a Cornu spiral:

In[5]:=
ResourceFunction["TotalSignedCurvature"][ Entity["PlaneCurve", "CornuSpiral"]["ParametricEquations"][a, b][ t], {t, a, b}]
Out[5]=

Properties and Relations (4) 

Define a hypotrochoid function:

In[6]:=
epitrochoid[a_, b_, h_] := {(a + b) Cos[#1] - h Cos[((a + b) #1)/b], (a + b) Sin[#1] - h Sin[((a + b) #1)/b]} & hypotrochoid[a_, b_, h_] := epitrochoid[a, -b, -h] hypotrochoid[2 k - 1, 1, k][t]
Out[7]=

The total signed curvature of a hypotrochoid:

In[8]:=
ResourceFunction["TotalSignedCurvature"][ hypotrochoid[5, 1, 3][t], {t, 0, b}]
Out[8]=

Plots of several hypotrochoids:

In[9]:=
GraphicsRow[ Table[ParametricPlot[ Evaluate[hypotrochoid[2 k - 1, 1, k][t]], {t, 0, 2 \[Pi]}, Axes -> False], {k, 2, 5}]]
Out[9]=

The total signed curvature is related to turning numbers:

In[10]:=
Table[ResourceFunction["TotalSignedCurvature"][ hypotrochoid[2 k - 1, 1, k][t], {t, 0, 2 \[Pi]}]/(2 \[Pi]), {k, 2, 5}]
Out[10]=
In[11]:=
Table[ResourceFunction["TurningNumber"][ hypotrochoid[2 k - 1, 1, k][t], {t, 0, 2 \[Pi]}], {k, 2, 5}]
Out[11]=

Publisher

Enrique Zeleny

Version History

  • 1.0.0 – 14 August 2020

Source Metadata

  • Citation:
    • Gray, A., Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, 1997.

Related Resources

License Information