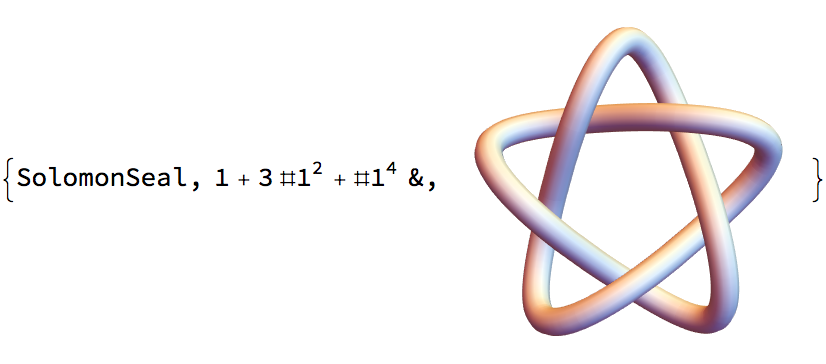Function Repository Resource:

TopolyFunction

Obtain topological information of polymers or biopolymers and other simple or complex structures

Contributed by: Wolfram Staff

ResourceFunction["TopolyFunction"][{"func",args,opts}]

returns the result of applying the topology function "func" to the specified arguments args using the options opts.

ResourceFunction["TopolyFunction"]["Information",comp]

gives an association with information about the component comp.

ResourceFunction["TopolyFunction"][…,session]

uses the specified running ExternalSessionObject session.

Details

ResourceFunction["TopolyFunction"] is a wrapper for the Python package Topoly. The package is installed automatically, as neccessary, using the the resource function PythonEvaluateWithDependencies.

ResourceFunction["TopolyFunction"] distinguishes knots, slipknots, links and spatial graphs through the calculation of topological polynomial invariants of a structure; identifies lasso types; creates minimal spanning surfaces; and generates random closed polymers.

The Python package Topoly and therefore ResourceFunction["TopolyFunction"] are not supported in Windows.

In ResourceFunction["TopolyFunction"][{"func",structure,…}] and ResourceFunction["TopolyFunction"][{"func",chain,…}], structure or chain can refer to a local or remote file or a Wolfram Language expression.

Files can be specified using a string giving a relative or absolute path to a local file, a File object or a URL object.

Accepted file formats include:

"XYZ"

coordinates in the three or four-column format (with index)

"PDB"

protein structure

"CIF"

crystallographic structure

"WL", "MATH"

coordinates in the Wolfram Language format

Accepted forms of expressions include:

{{x₁,y₁,z₁},…}

list of coordinates

"pdcode"

planar diagram code string

"emcode"

Ewing–Millett code string

Planar diagram (PD) code and Ewing–Millett (EM) codes are explained in the PD code and EM code section of the Topoly Dictionary.

Structures can be modified using the following functions:

"StructureClose"

connects loose ends

"StructureReduce"

reduces the number of crossings

Functions that are capable of automatically performing structure modifications accept the options "Closure" and "ReductionMethod" with the same option values as "StructureClose" and "StructureReduce", respectively.

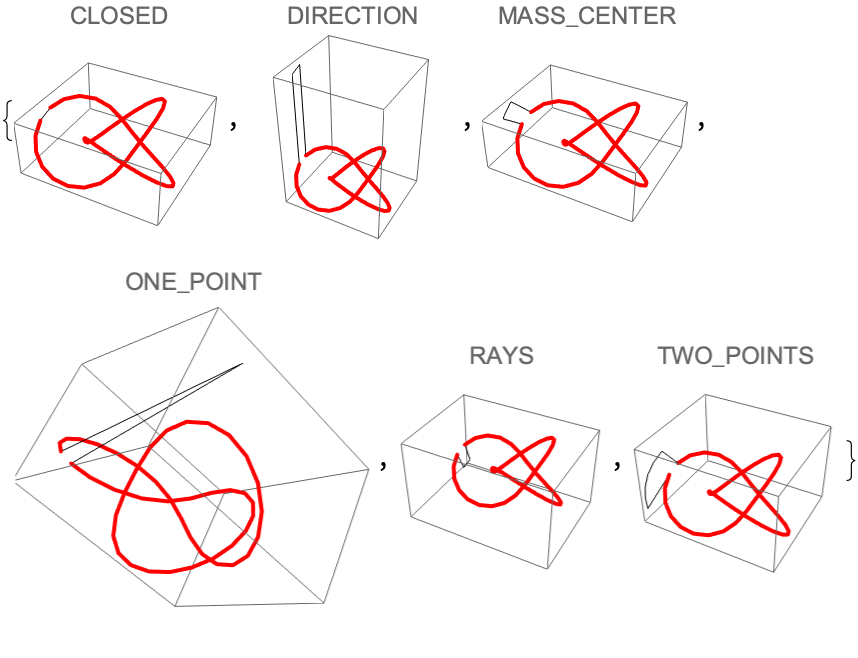
The method for connecting loose ends is chosen using the "Closure" option, which involves either a straight line or a path along an encompassing sphere with the center at the geometric center of the structure. The available methods include:

"CLOSED"

straight line

"MASS_CENTER"

endpoints projections in the direction from the center of mass

"DIRECTION"

parallel segments from the endpoints in a chosen direction

"ONE_POINT"

the endpoints connected to a single randomly chosen point

"TWO_POINTS"

two random points (default)

"RAYS"

parallel segments from the endpoints in a random direction

The structure reduction method is chosen usign the option "ReductionMethod" with the following possible values:

"KMT"

Koniaris–Muthukumar–Taylor algorithm

"REIDEMEISTER"

Reidemeister moves

"EASY"

deterministic Reidemeister moves

ResourceFunction["TopolyFunction"]["Properties"] gives a list of the available function properties.

Functions for calculating topological invariants include:

"AlexanderPolynomial"

Alexander polynomial

"APSBracket"

APS bracket

"BLMHoPolynomial"

BLM/Ho polynomial

"ConwayPolynomial"

Conway polynomial

"HOMFLYPolynomial"

HOMFLY polynomial

"JonesPolynomial"

Jones polynomial

"KauffmanBracket"

Kauffman bracket

"KauffmanPolynomial"

Kauffman two-variable polynomial

"Writhe"

writhe

"YamadaPolynomial"

Yamada polynomial

With the default value of the option "Matrix"→False, invariant functions generally return the topology type for deterministic values of the option "Closure" and an association of topology types and their probabilities for randomized values of "Closure". For "Matrix"→True, these values are returned in an association with subchain indices as keys.

When detected, the polynomial notations for topology type strings returned by the Python code are converted to Wolfram Language expressions as follows:

"n_k"

Alexander–Briggs notation n_k

"i₁ i₂ i₃…"

polynomial coefficient lists {i₁,i₂,i₃,…}

"polynomial"

polynomial as a pure function

Functions for analyzing subchain topology include:

"GaussLinkingNumber"

Gauss linking number (GLN) between two chains

"FindSpots"

centers of fields in the knotting fingerprint matrix

"MatrixConvert"

converts between fingeprint matrix formats

Functions for the lasso type identification include:

"LassoType"

lasso types for loops

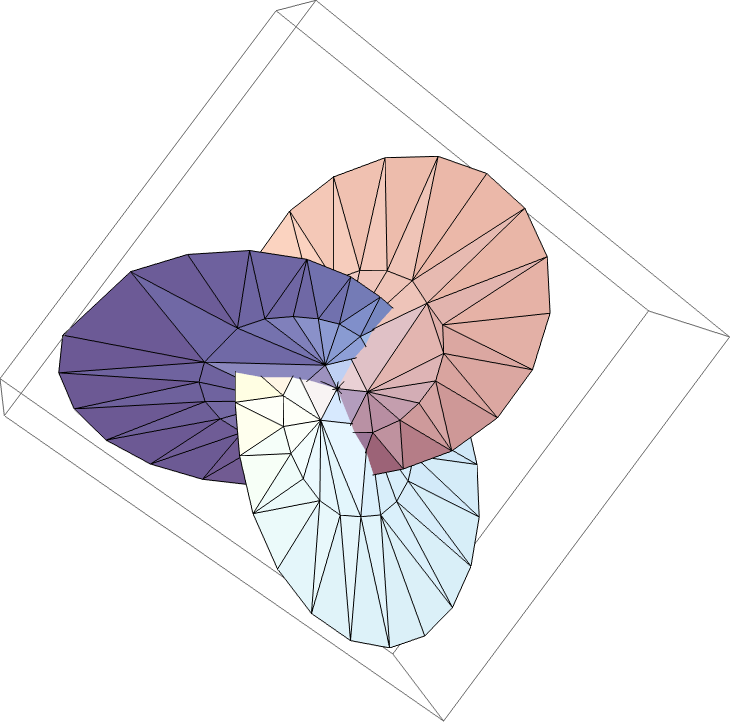
"MinimalSurfaceMesh"

triangulated minimal surface spanning a loop

Functions for finding loops, links, theta-curves and handcuffs include:

"FindLoops"

loops

"FindLinks"

links

"FindThetas"

theta-curves

"FindHandcuffs"

handcuffs

Functions for converting between different structure representations include:

{"TopologyTypeToPDCode","type"}

topology type to PD code

{"StructureConvert","code"}

PD code to EM code and vice versa

{"CoefficientsToTopologyType",coef,"invariant"}

polynomial coefficients to topology type

Coefficients coef can be given as:

{c₁,c₂,…}

list

"c₁ c₂ …"

string of space-delimited coefficients

<|coef₁→prob₁,…|>

association of coefficients and their probabilities

Possible specifications for "invariant" include:

"Alexander"

Alexander polynomial

"Jones"

Jones polynomial

"Conway"

Conway polynomial

"HOMFLY"

HOMFLY polynomial

"Yamada"

Yamada polynomial

"APS"

APS bracket

Functions that generate coordinates of n random polygons include:

{"RandomWalk",k,n}

k-step random walks

{"RandomLoop",k,n}

length k loops

{"RandomLasso",k,l,n}

lassos with loop length of k and tail length of l

{"RandomHandcuff",{k,l},m,n}

handcuffs with loops of length k and l and tail length of m

{"RandomLink",{k,l},d,n}

loop pairs of length k and l and distance between their geometric centers of d

In ResourceFunction["TopolyFunction"]["Information",comp,…], comp can be a function name or a parameter class. Possible elements of the returned association include:

"Arguments"

arguments of the function

"Options"

options of the function

"Values"

possible values of the component

ResourceFunction["TopolyFunction"]["PropertyRules"] provides a mapping between the property names and the underlying Python-side names.

ResourceFunction["TopolyFunction"]["RawInformation",func,…] returns a string representing the Python-side help for the function func.

In ResourceFunction["TopolyFunction"], strings representing function names, option names and option values can be given as either property names or Python-side names.

Examples

Basic Examples (4)

Obtain the topological type of a knot given a list of spatial coordinates:

In[1]:=

In[2]:=

Out[2]=

In[3]:=

Out[3]=

Download a PDB file for the human obesity protein 1AX8 from the RCSB server:

In[4]:=

Display the molecule:

In[5]:=

Out[5]=

Find all the loops in the structure:

In[6]:=

Out[6]=

Display the loops (in this case, a single loop):

In[7]:=

Out[7]=

Construct a wireframe of a minimal surface spanning a chain representing a knot:

In[8]:=

Construct the minimal surface mesh:

In[9]:=

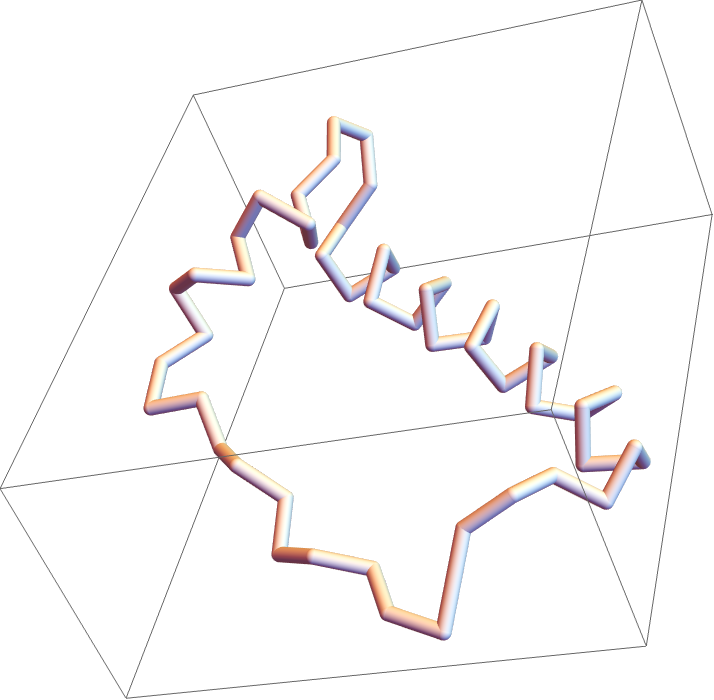
mesh = ResourceFunction[
"TopolyFunction"][{"MinimalSurfaceMesh", coordinates, "LoopIndices" -> {1, Length[coordinates]}}]

Out[9]=

Obtain a list of coordinates for triangles that form the mesh:

In[10]:=

Out[10]=

Display the triangles:

In[11]:=

Out[11]=

Generate random lasso structures:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Scope (29)

Accepted structures: Local or remote files (4)

Use a local PDB file (in this case, downloaded from a URL):

In[14]:=

Out[14]=

In[15]:=

Out[15]=

Use a remote file directly by specifying its URL:

In[16]:=

Out[16]=

Give file specification as a string representing the absolute path to the file:

In[17]:=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

Use a path relative to the current working directory:

In[20]:=

In[21]:=

Out[21]=

Reset directory to clean up:

In[22]:=

Accepted structures: File formats (4)

Use a PDB file:

In[23]:=

Out[23]=

Use a CIF file:

In[24]:=

Out[24]=

Use an XYZ file:

In[25]:=

$ResourceFunction[ "TopolyFunction"][{"AlexanderPolynomial", URL["https://people.math.sc.edu/Burkardt/data/xyz/helix_201.xyz"], "Closure" -> "CLOSED"}]$

Out[25]=

Use a file containing a string representing a Wolfram Language list of coordinates:

In[26]:=

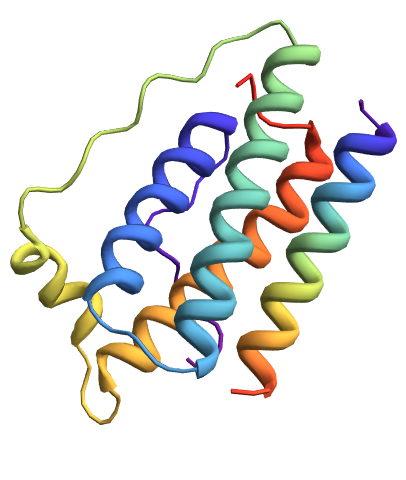
$ResourceFunction[ "TopolyFunction"][{"AlexanderPolynomial", URL["https://raw.githubusercontent.com/ilbsm/topoly_tutorial/master/data/1j85.math"], "Closure" -> "CLOSED"}]$

Out[26]=

Accepted structures: Expressions (4)

Use a Wolfram Language list of 3D coordinates:

In[27]:=

In[28]:=

Out[28]=

Use coordinates with indices:

In[29]:=

In[30]:=

Out[30]=

Use a PD code string:

In[31]:=

Out[31]=

Use an EM code string:

In[32]:=

Out[32]=

Structure manipulation (2)

Define an auxiliary function to display a closed curve and connect loose ends of a structure using different methods:

In[33]:=

$joinEnds[{f_, rest___}] := {f, rest, f}$

In[34]:=

In[35]:=

Table[Graphics3D[{Line[
joinEnds@ ResourceFunction[
"TopolyFunction"][{"StructureClose", coordinates, "Closure" -> closure}]], {Thick, Red, Line[coordinates]}}, PlotLabel -> closure], {closure, ResourceFunction["TopolyFunction"]["Information", "Closure"][
"Values"]}]

Out[35]=

Obtain randomized closures using one of the last three methods:

In[36]:=

In[37]:=

Out[37]=

Function list (2)

Available property functions:

In[38]:=

Out[38]=

Arguments and options of a function:

In[39]:=

Out[39]=

Topological invariants (3)

Given a list of coordinates of a structure, determine its topology by calculating the Alexander polynomial:

In[40]:=

In[41]:=

Out[41]=

In[42]:=

Out[42]=

Find polynomial coefficients:

In[43]:=

Out[43]=

Find the explicit pure-function form of the Alexander polynomial for the knot:

In[44]:=

Out[44]=

Given the same structure, find the pure-function forms of the different invariants:

In[45]:=

In[46]:=

Table[{poly, ResourceFunction[
"TopolyFunction"][{poly, coordinates, "ReducedPolynomials" -> False, "Translate" -> False, "Closure" -> "CLOSED"}]}, {poly, Select[ ResourceFunction["TopolyFunction"]["Properties"], StringContainsQ[#, "Polynomial"] &]}] // Grid

Out[46]=

Use the default (stochastic) method to find the probabilities of different topologies:

In[47]:=

In[48]:=

Out[48]=

List the most probable topology first:

In[49]:=

Out[49]=

Subchain topology: Fingerprint matrix (6)

Construct a list of coordinates of a 5₁ knot:

In[50]:=

Out[50]=

In[51]:=

In[52]:=

Out[52]=

Find the subchain matrix in the form of an association, storing the fingerprint matrix in the home directory:

In[53]:=

In[54]:=

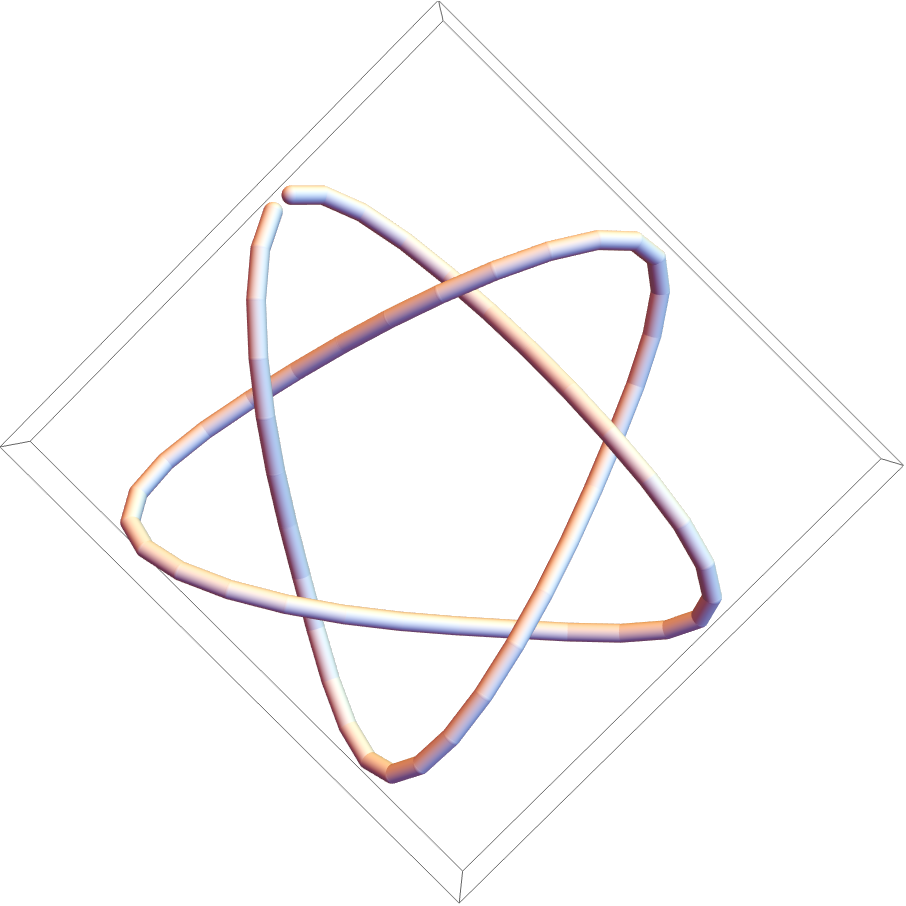
PrintTemporary["This may take a while..."];
(assoc = ResourceFunction[
"TopolyFunction"][{"ConwayPolynomial", coordinates51, "Tries" -> 10, "Matrix" -> True, "MatrixMap" -> True, "MapFilename" -> filename}]) // Short

Out[54]=

Combine inner associations of the subchains into sparse arrays for each topology:

In[55]:=

Out[55]=

Find representative subchains:

In[56]:=

Out[56]=

Plot fingerprint matrices of the representative subchains:

In[57]:=

Out[57]=

Obtain a Topoly plot of the fingerprint matrix:

In[58]:=

Out[58]=

Subchain topology: Gauss linking number (2)

Download coordinates of the Hopf link from the Knot Server and obtain a representation of the linked chains:

In[59]:=

Out[59]=

In[60]:=

Out[60]=

In[61]:=

Out[61]=

Find the Gauss linking number (GLN) between the chains:

In[62]:=

Out[62]=

Reversing one of the chains changes the sign of the Gauss linking number:

In[63]:=

Out[63]=

Create a matrix of GLN values between link1 and all possible subchains of link2:

In[64]:=

Out[64]=

Plot the matrix:

In[65]:=

Out[65]=

Obtain a Topoly plot of the same matrix, saved under a chosen filename in the home directory:

In[66]:=

In[67]:=

Out[67]=

In[68]:=

Out[68]=

External session (2)

Make several calls to TopolyFunction in the same external session:

In[73]:=

Out[73]=

In[74]:=

In[75]:=

Out[75]=

In[76]:=

Out[76]=

End the session:

In[77]:=

Options (3)

OutputType (3)

Possible values of some common options:

In[78]:=

Out[78]=

In[79]:=

Out[79]=

In[80]:=

Out[80]=

With the default "OutputType"→"Mathematica", the result is in the Wolfram Language List format:

In[81]:=

Out[81]=

Obtain some debugging information:

In[82]:=

In[83]:=

Out[83]=

Applications (2)

TopolyFunction can calculate knot topology for UCH protein (PDB code 2len, chain A, model 2).

First, obtain a PDB file from the RCSB server:

In[84]:=

Out[84]=

In[85]:=

Out[85]=

Using the Conway polynomial, obtain the statistics of knots occurring in different closures:

In[86]:=

Out[86]=

Arrange in the order of probabilities:

In[87]:=

Out[87]=

Display a histogram of discovered knots in the protein:

In[88]:=

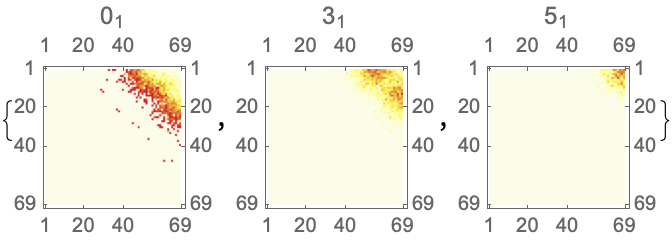
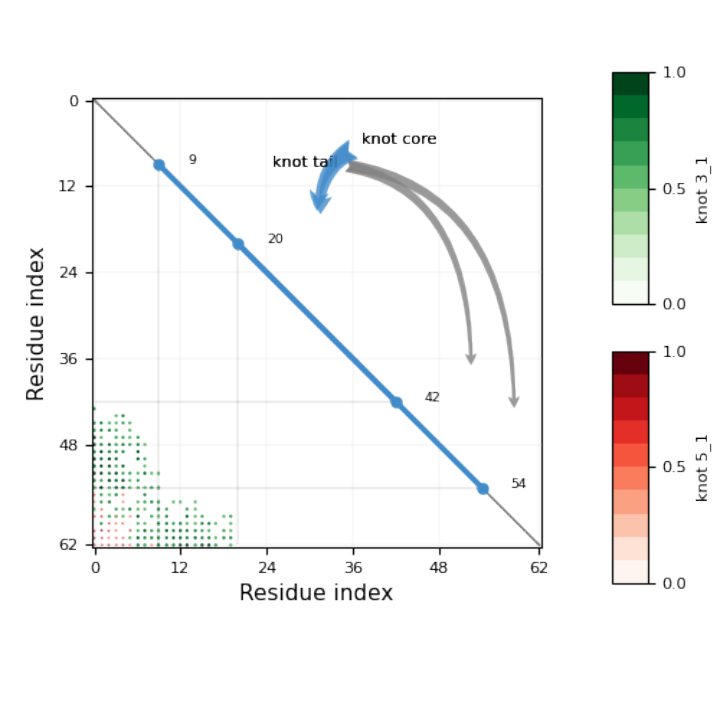
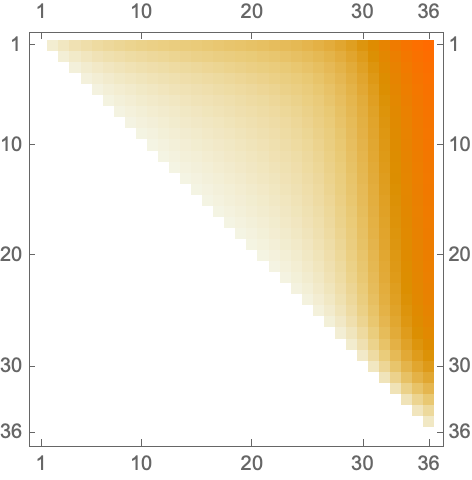
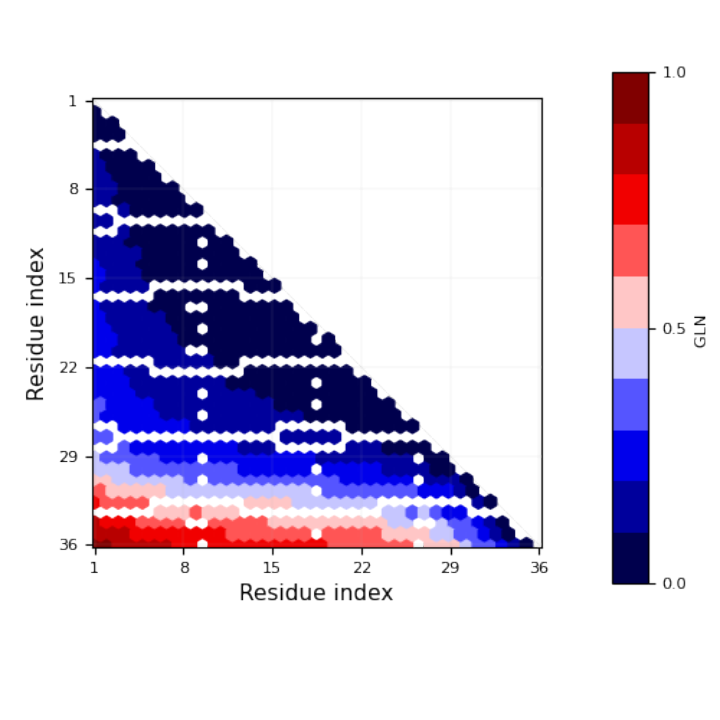
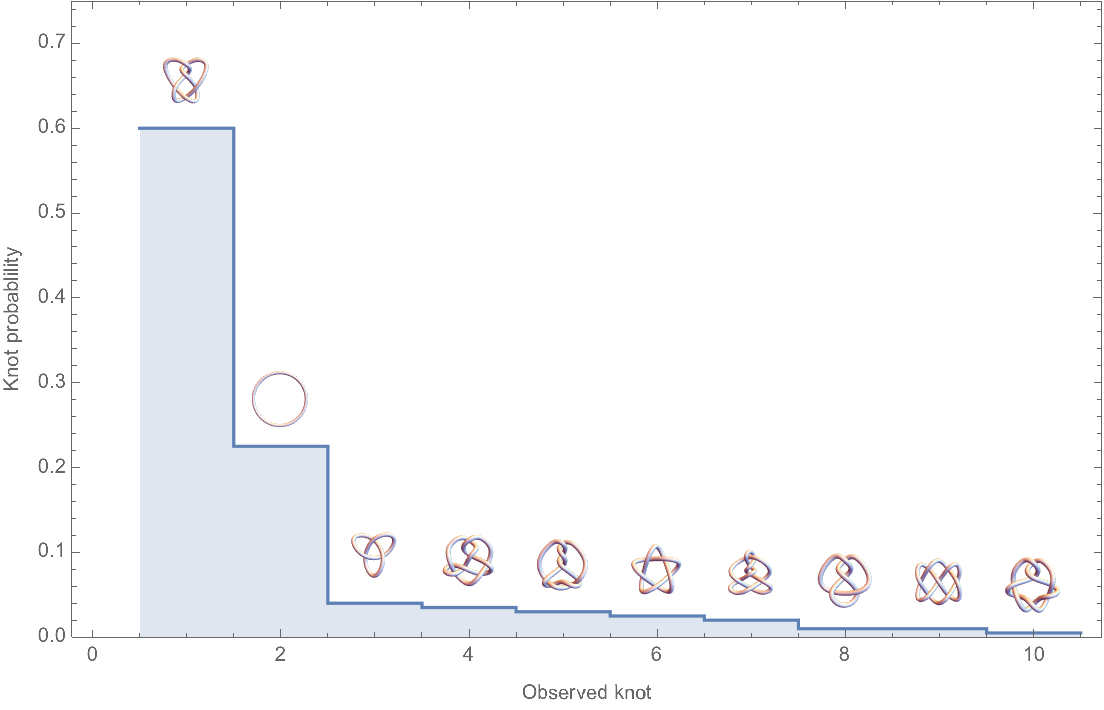
$Module[{keys = Keys[stats], iconF}, iconF[sub_Subscript] := KnotData[List @@ sub]; iconF[_] := ""; ListStepPlot[KeyValueMap[Labeled[#2, iconF[#], Top] &, stats], Center, Ticks -> {Transpose[{Range[Length[keys]], keys}], Automatic}, PlotRangePadding -> {Automatic, {0, 0.15}}, Filling -> Bottom, Frame -> True, FrameLabel -> {"Observed knot", "Knot probablility"}]]$

Out[88]=

TopolyFunction can calculate the lasso types for all the loops in cerato-platanin (PDB code 3sum).

First, obtain a PDB file from the RCSB server:

In[89]:=

Out[89]=

In[90]:=

Out[90]=

Find lasso types for the loops in the structure:

In[91]:=

Out[91]=

Obtain additional information about the lassos:

In[92]:=

Out[92]=

In[93]:=

Out[93]=

Plot the minimal spanning surfaces for each loop:

In[94]:=

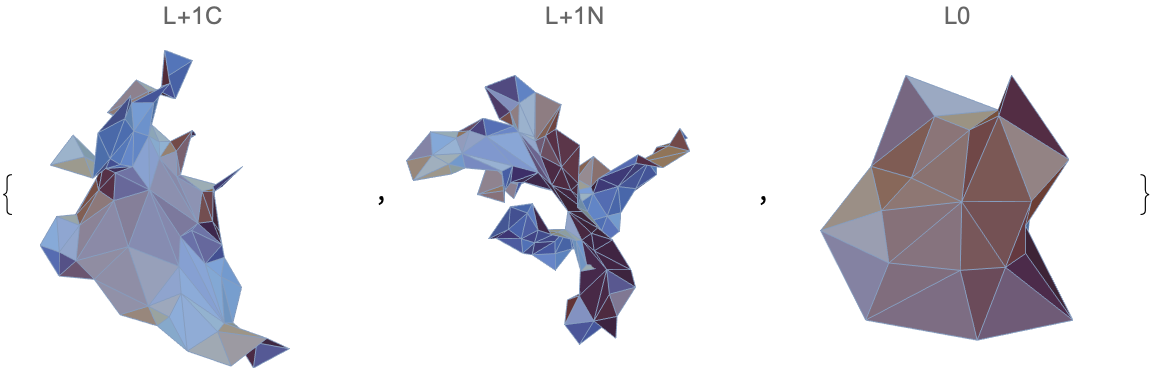
meshes = KeyValueMap[
Show[ ResourceFunction[
"TopolyFunction"][{"MinimalSurfaceMesh", file, "LoopIndices" -> #}], PlotLabel -> #2["class"]] &, lassos]

Out[94]=

Properties and Relations (4)

TopolyFunction finds topology information given spatial coordinates of a curve, while some additional information for known knots can then be found with KnotData:

In[95]:=

In[96]:=

Out[96]=

In[97]:=

Out[97]=

In[98]:=

Out[98]=

The mapping between the curated TopolyFunction names and the Python-side names:

In[99]:=

Out[99]=

Python-side help of a function:

In[100]:=

Out[100]=

Python-side names, such as given in the Topoly documentation or available in the literature, can be used in TopolyFunction directly:

In[101]:=

In[102]:=

Out[102]=

Compare with the corresponding curated names:

In[103]:=

Out[103]=

Version History

1.0.0 – 27 July 2021

Source Metadata

Citation:
- Dabrowski-Tumanski, P., Rubach, P., Niemyska, W., Ambrozy Gren, B., Ida Sulkowska, J., "Topoly: Python package to analyze topology of polymers." Briefings in Bioinformatics, vol. 22, no. 3, 1–8, 2021. DOI: https://doi.org/10.1093/bib/bbaa196
- Sułkowska, J.I., Rawdon, E.J., Millett, K.C., Onuchic, J.N., Stasiak, A., "Conservation of complex knotting and slipknotting patterns in proteins." Proceedings of the National Academy of Sciences, vol. 109, no. 26, E1715–E1723, 2012. DOI: https://doi.org/10.1073/pnas.1205918109

Related Resources

Author Notes

There's no Windows distribution of Topoly at the moment (June 2021), but there might be a way to use the TopolyDetect on Windows via WSL.

Currently includes only documented top-level Topoly functions. Does not include classes (AlexanderGraph, ConwayGraph, etc.); or polynomial classes (Alexander, etc. and their import/export). Also does not support plotting functions plot_graph, plot_matrix, etc.) and a few others (topoly.create and topoly.is_aa).

The documentation is static. It will need to be updated for future versions of Topoly. The information returned with "Information" and "RawInformation", on the other hand, is dynamic, retrieved from the Python side in each WL session.

The current documentation is sketchy. TopolyFunction["RawInformation",…] is intended to partially alleviate the pain.

The option "Output" is not currently supported.

Some other options should benefit from specific pre- and post-processing.

Option values are not curated strings yet.

Directory setting, and random seed does not currently affect the Python side. The latter is especially important as one would often want stochastic methods to be reproducible.

Not all topology strings are currently parsed (e.g. , composite knots "3_1#3_1" or "3_1#3_1|8_20" would require typesetting, etc.).

Also, not all polynomial coefficients are given in a usable WL forms, eg (for 3₁):

Some function do not seem to accept certain PDB files, while accepting others:

There must be some incantation to obtain integer numbers in the GLN examples above .

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

TopolyFunction

Details

Examples

Basic Examples (4)

Scope (29)

Accepted structures: Local or remote files (4)

Accepted structures: File formats (4)

Accepted structures: Expressions (4)

Structure manipulation (2)

Function list (2)

Topological invariants (3)

Subchain topology: Fingerprint matrix (6)

Subchain topology: Gauss linking number (2)

External session (2)

Options (3)

OutputType (3)

Applications (2)

Properties and Relations (4)

Related Links

Version History

Source Metadata

Related Resources

Author Notes

License Information

TopolyFunction

Details

Examples

Basic Examples (4)

Scope (29)

Accepted structures: Local or remote files (4)

Accepted structures: File formats (4)

Accepted structures: Expressions (4)

Structure manipulation (2)

Function list (2)

Topological invariants (3)

Subchain topology: Fingerprint matrix (6)

Subchain topology: Gauss linking number (2)

External session (2)

Options (3)

OutputType (3)

Applications (2)

Properties and Relations (4)

Related Links

Version History

Source Metadata

Related Resources

Related Symbols

Author Notes

License Information