Function Repository Resource:

ToPythonFunction (1.0.0) current version: 1.1.0 »

Source Notebook

Convert a Wolfram Language function to a Python function

Contributed by: Igor Bakshee

ResourceFunction["ToPythonFunction"][func]

gives a string of Python code corresponding to the Wolfram Language function func.

ResourceFunction["ToPythonFunction"][session,func,…]

deploys the function in the running Python session and returns an ExternalFunction object.

Details and Options

Supported types of functions func include:

body&

pure functions in formal parameters #,#2,…

Function[{x,y,…},body,…]

pure functions in named arguments

function f defined in the Wolfram Language or C code

"code"

Python code string

The following options can be given:

Method

Automatic

method to use

Prolog

{}

Python commands executed before deploying the function

Epilog

{}

Python functions applied to the result

If the function func is specified as a Python code string, all options of ResourceFunction["ToPythonFunction"] are ignored with the exception of Prolog.

Possible values for the Method option include:

"BuiltIns"

attempt to use Python built-in functions and the standard library

"Callback"

execute a callback to the Wolfram Language session

"numpy" or "np"

use the numpy package, if possible; otherwise "BuiltIns"

Automatic

"BuiltIns", if possible; otherwise "Callback"

The method "BuiltIns" currently supports only pure functions and functions defined by a single downvalue f[x_,y_,…]:=body ; further, the function body can contain only elementary mathematical functions, with no restrictions on arguments, nor can the function have optional arguments, options or attributes.

The method "Callback" supports arbitrary functions.

In ResourceFunction["ToPythonFunction"][…,func,domain,…], domain specifies which of the built-in modules to use for the conversion. Possible values include:

Reals

use the "math" module

Complexes

use the "cmath" module

Automatic

determine heuristically

The default Automatic domain resolves to Reals if the function body does not explicitely contains complex numbers; otherwise to Complexes.

If the heuristic for Method→"BuiltIns" fails to automatically convert Wolfram Language code to Python code, you might still be able to convert the code and deploy a Python function manually.

For Method→"Callback", the Python code string is defined in terms of the Wolfram Lamguage session variable "wl_session", which can be created on the Python side as "from wolframclient.evaluation import WolframLanguageSession; wl_session = WolframLanguageSession()".

ResourceFunction["ToPythonFunction"][f,Method→"Callback",…] can return a list in the form {"def","setup"}, where "def" is a string representing the Python-side definition of the function f and "setup" is a Python code string to be executed before calling the function.

Examples

Basic Examples (2)

Convert a pure function to a Python lambda function:

In[1]:=

Out[1]=

Deploy a Wolfram Language function in a Python session:

In[2]:=

Out[2]=

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Evaluate the function value in Python:

In[5]:=

Out[5]=

Compare with the result in the Wolfram Language:

In[6]:=

Out[6]=

Clean up by closing the Python session:

In[7]:=

Scope (9)

Elementary functions are convertible to Python using the Python standard library:

In[8]:=

Out[8]=

Special functions are computed by a Wolfram Language callback:

In[9]:=

Out[9]=

Pure functions in formal parameters # (#1), #2,…:

In[10]:=

Out[10]=

In[11]:=

Out[11]=

Pure functions in named arguments:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

Vector arguments:

In[14]:=

Out[14]=

Built-in Wolfram Language functions:

In[15]:=

Out[15]=

User-defined functions:

In[16]:=

In[17]:=

Out[17]=

Python code strings:

In[18]:=

Out[18]=

In[19]:=

Out[19]=

In[20]:=

Out[20]=

In[21]:=

Specify whether to use "math" or "cmath" module on the Python side by giving the optional argument domain:

In[22]:=

Out[22]=

In[23]:=

Out[23]=

Decide heuristically, depending whether the function body contains explicit complex values:

In[24]:=

Out[24]=

In[25]:=

Out[25]=

Options (7)

Method (4)

Use a Python-side function from the standard library:

In[26]:=

Out[26]=

Implement a callback into a WolframLangauge session to compute the function:

In[27]:=

Out[27]=

Use the Python package numpy:

In[28]:=

Out[28]=

Use the default heuristic to decide between the methods:

In[29]:=

Out[29]=

In[30]:=

Out[30]=

Prolog (1)

Use the Prolog option to ensure that the Python interpreter meets the requirements before deploying the function:

In[31]:=

Out[31]=

In[32]:=

$ResourceFunction["ToPythonFunction"][session, # &, Prolog -> {"import sys", "if sys.version_info.major<5: raise ValueError('Insufficient Python version')"}]$

Out[32]=

In[33]:=

Epilog (2)

Create a function which returns a Python array:

In[34]:=

Out[34]=

In[35]:=

Out[35]=

In[36]:=

Out[36]=

Use the Epilog option to convert the result to numpy.array:

In[37]:=

Out[37]=

In[38]:=

Out[38]=

In[39]:=

Out[39]=

In[40]:=

Applications (4)

Functional Programming (4)

Start a Python session and create a PythonObject for the Probabilistic Numerics Python package ProbNum:

In[41]:=

Out[41]=

In[42]:=

Out[42]=

Deploy a Python function describing an ODE vector field:

In[43]:=

Out[43]=

Pass the deployed Wolfram Language function f back to Python as a field to solve the logistic ODE:

In[44]:=

In[45]:=

Out[45]=

Plot the solution:

In[46]:=

ListPlot[Transpose[
Normal@{Normal[solution["locations"]], Flatten[Normal[
ResourceFunction["PythonObject"][solution, "states", True][
"mean"]]]}]]

Out[46]=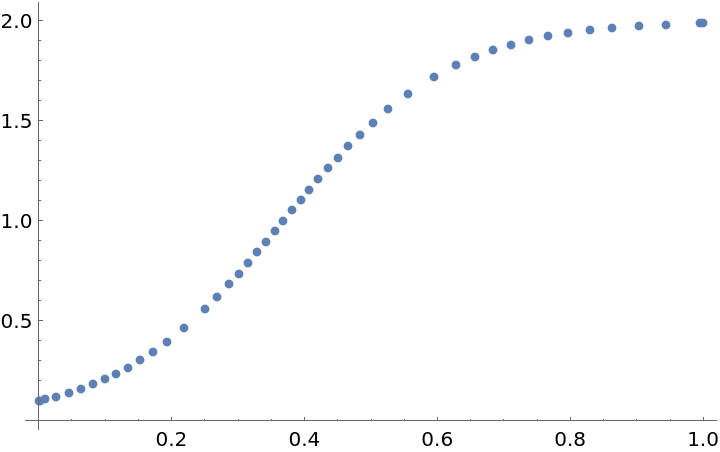

In[47]:=

Properties and Relations (5)

Callback functions contain a template slot for the Wolfram Language session defined on the Python side:

In[48]:=

Out[48]=

Given such a string as an argument, ToPythonFunction automatically fills the slot with the variable wl_session defined in the Python session:

In[49]:=

Out[49]=

In[50]:=

Out[50]=

Alternatively, you can fill the slot with the name of another variable of your choice:

In[51]:=

$ResourceFunction["ToPythonFunction"][session, TemplateApply[str, "my_session"], Prolog -> {"from wolframclient.evaluation import WolframLanguageSession", "my_session=WolframLanguageSession()"}]$