Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ToNegabinary

Source Notebook

Get the negabinary representation of an integer

Contributed by: Eric W. Weisstein

ResourceFunction["ToNegabinary"][n]

gives the negabinary representation of the integer n.

Details

Negabinary is a representation of an integer in base –2.

Examples

Basic Examples (4) 

Get the representation for 17 in negabinary:

In[1]:=
ResourceFunction["ToNegabinary"][17]
Out[1]=

From this representation, recover the original integer:

In[2]:=
FromDigits[%, -2]
Out[2]=

Use the resource function FromNegabinary:

In[3]:=
ResourceFunction["FromNegabinary"][ ResourceFunction["ToNegabinary"][17]]
Out[3]=

Some integers have the same representation in base 2:

In[4]:=
IntegerDigits[17, 2]
Out[4]=

Scope (1) 

ToNegabinary handles negative numbers:

In[5]:=
ResourceFunction["ToNegabinary"][-5]
Out[5]=

Applications (2) 

Plot the negabinary representation for the first 22 integers:

In[6]:=
ArrayPlot[ PadLeft[Reverse@ Flatten[Table[ ResourceFunction["ToNegabinary"][n], {n, 85}], {{2}, {1}}], Automatic, None], ColorRules -> {0 -> Gray}, Frame -> False]
Out[6]=

A table of integers and their negabinary representations:

In[7]:=
Grid[Map[Text, Join[{{"n", "(-2\!\(\*SuperscriptBox[\()\), \(4\)]\)=16", "(-2\!\(\*SuperscriptBox[\()\), \(3\)]\)=-8", "(-2\!\(\*SuperscriptBox[\()\), \(2\)]\)=4", "(-2\!\(\*SuperscriptBox[\()\), \(1\)]\)=-2", "negabinary"}}, Table[Flatten[{n, PadLeft[ResourceFunction["ToNegabinary"][n], 4], Row[ResourceFunction["ToNegabinary"][n]]}], {n, -5, 5}]], {2}], Alignment -> Right, Frame -> All]
Out[7]=

Properties and Relations (1) 

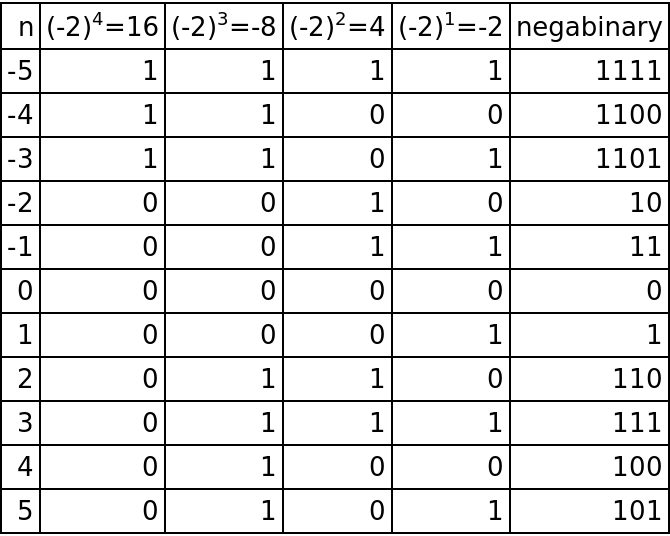Numbers belonging to the Moser–de Bruijn sequence have identical binary and negabinary representations:

In[8]:=
md[n_] := FromDigits[IntegerDigits[n, 2], 4]
In[9]:=
Table[md[n], {n, 20}]
Out[9]=
In[10]:=
Table[IntegerDigits[md[n], 2] === ResourceFunction["ToNegabinary"][md[n]], {n, 20}]
Out[10]=

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 31 August 2021
  • 1.0.0 – 11 February 2019

Source Metadata

  • Citation:
    • Schroeppel, R. Item 128 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 24, Feb. 1972.
      Available from http://www.inwap.com/pdp10/hbaker/hakmem/flows.html#item128
    • Szudzik, M. "Programming Challenge: A Mathematica Programming Contest." Wolfram Technology Conference, 1999.
      Available from https://library.wolfram.com/infocenter/Conferences/4829/Dev1999Contest.nb?file_id=4554

Related Resources

Author Notes

The implementation used here is adapted from code due to David Librik.

License Information