Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate the time to fall from a specified height
ResourceFunction["TimeToFallFormula"][h] returns the time taken for an object to fall vertically from a distance h without drag. | |
ResourceFunction["TimeToFallFormula"][h,assoc] returns the time taken for an object to fall vertically from a distance h with drag parameters in the Association assoc. | |
ResourceFunction["TimeToFallFormula"][property] returns the specified property of the time to fall formula. |
| "DragCoefficient" | 0.5 | resistance of the object falling in the fluid |
| "Area" | 20 cm2 | the object's projected area |
| "Mass" | 3 kg | the object's mass |
| "Density" | 1.29 kg/m3 | the fluid's density |
| "FormulaWithDrag" | equation for time to fall with drag |
| "FormulaWithoutDrag" | equation for time to fall without drag |
| "QuantityVariableNames" | English names for all variables |
Calculate the time to fall without drag:
| In[1]:= |
| Out[1]= |
Calculate the time to fall considering drag:
| In[2]:= | ![ResourceFunction["TimeToFallFormula"][
Quantity[200, "Meters"], <|"DragCoefficient" -> 0.5, "Area" -> Quantity[20, ("Centimeters")^2], "Mass" -> Quantity[2.89, "Kilograms"], "Density" -> Quantity[1.5, ("Kilograms")/("Meters")^3]|>]](https://www.wolframcloud.com/obj/resourcesystem/images/69c/69c997e8-3136-4112-887b-cef7b0c277fc/4b23ffe20c9b7ac8.png) |
| Out[2]= |
Show the formula used with drag:
| In[3]:= |
| Out[3]= |
and without drag:
| In[4]:= |
| Out[4]= |
Find the name of the quantity variables used by TimeToFallFormula:
| In[5]:= |
| Out[5]= |
TimeToFallFormula is listable:
| In[6]:= |
| Out[6]= |
Use "Gravity" to specify the value of the gravity used:
| In[7]:= |
| Out[7]= |
Plot the time that it would take to fall from the highest mountain of each continent:
| In[9]:= | ![highestMountainHeights = EntityValue[
EntityClass[
"Mountain", {EntityProperty["Mountain", "Elevation"] -> TakeLargest[1], EntityProperty["Mountain", "Continent"] -> EntityClass["GeographicRegion", "Continents"]}], "Elevation", "EntityAssociation"];
highestMountainsTimeToFall = ResourceFunction["TimeToFallFormula"][highestMountainHeights];
GeoBubbleChart[
MapIndexed[Tooltip[#1, Column[{#2[[1, 1]], #1}]] &, highestMountainsTimeToFall], BubbleSizes -> {.1, .4}]](https://www.wolframcloud.com/obj/resourcesystem/images/69c/69c997e8-3136-4112-887b-cef7b0c277fc/1100e882c22bf930.png) |
| Out[11]= | 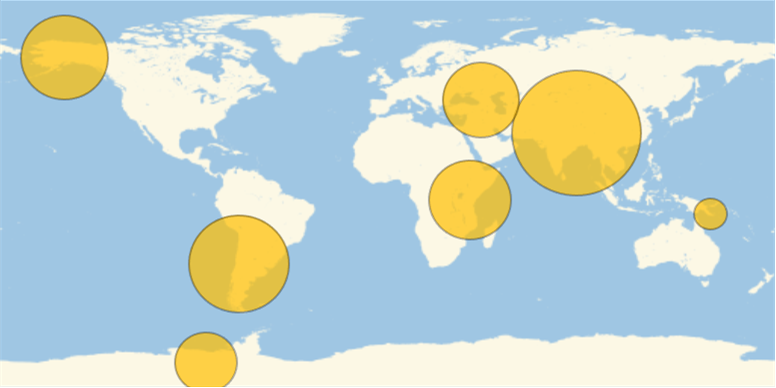 |
Plot the time that it would take to fall the height of the Empire State Building on each planet in the solar system:
| In[12]:= | ![BarChart[ResourceFunction["TimeToFallFormula"][
Entity["Building", "EmpireStateBuilding::h583b"]["Height"], "Gravity" -> #] & /@ EntityClass["Planet", All]["Gravity"], ChartStyle -> EntityValue[
EntityClass["Planet", All][EntityProperty["Planet", "Color"]], "Value"], ChartLabels -> EntityClass["Planet", All]["Name"], TargetUnits -> Automatic, AxesLabel -> "Time (s)"]](https://www.wolframcloud.com/obj/resourcesystem/images/69c/69c997e8-3136-4112-887b-cef7b0c277fc/43c8fe130612bb9a.png) |
| Out[12]= | 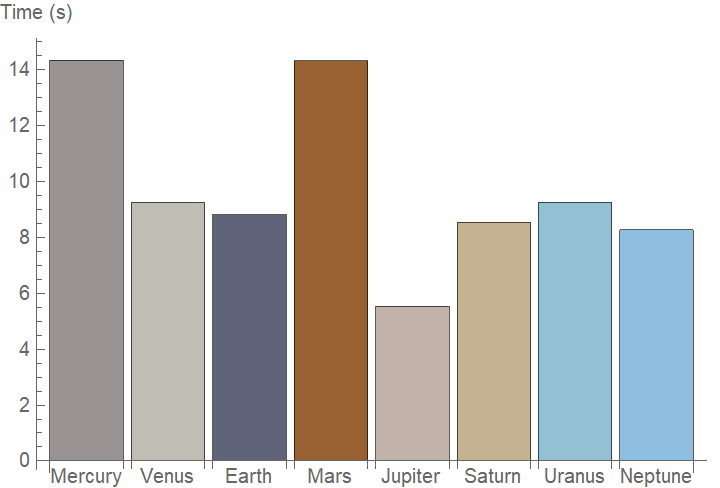 |
This work is licensed under a Creative Commons Attribution 4.0 International License